Контрольная группа. Сравнение результатов для фона и после воздействия

+3 +3 +3

= 0,39.

V

/(15 х 55)-3² /825-9 /58,28

15- 1 14

' Все эти расчеты необходимо сделать в чисто учебных целях. Сегодня существуют более быстрые методы, при которых основная работа сводится к вводу данных в программируемый микрокалькулятор или в компьютер, который автоматически выдает результат. Приведенная здесь таблица помогает понять все расчеты, которые осуществляются такими машинами.

Статистика и обработка данных 301

Величина t = 0,39 ниже той, которая необходима для уровня значимости 0,05 при 14 степенях свободы. Иными словами, порог вероятности для такого / выше 0,05. Таким образом, нулевая гипотеза не может быть отвергнута, и разница между выборками недостоверна. В сокращенном виде это записывается следующим образом:

t = 0,39; г| = 14; Р > 0,05; недостоверно.

Теперь попробуйте самостоятельно применить метод Стьюдента для зависимых выборок к обоим распределениям опытной группы с учетом того, что вычисление частных разностей для пар дало следующие результаты:

•Ld= -59 и ~Ld² =349;

Значение t ...... чем то, которое соответствует уровню значимости 0,05

для ..... степеней свободы. Значит, нулевая гипотеза ...... а различие

между выборками .....

Запишите это в сокращенном виде.

Дисперсионный анализ (тест F Снедекора)

Метод Снедекора - это параметрический тест, используемый в тех случаях, когда имеются три или большее число выборок. Сущность этого метода заключается в том, чтобы определить, является ли разброс средних для различных выборок относительно общей средней для всей совокупности данных достоверно отличным от разброса данных относи­тельно средней в пределах каждой выборки. Если все выборки принадле­жат одной и той же популяции, то разброс между ними должен быть не больше, чем разброс данных внутри их самих.

В методе Снедекора в качестве показателя разброса используют вариансу (дисперсию). Поэтому анализ сводится к тому, чтобы сравнить вариансу распределений между выборками с вариансами в пределах каждой выборки, или:

(<, =, > ?) 0,05; различие

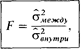
где с^рж.ву- варианса средних каждой выборки относительно общей средней;

внутри- варианса данных внутри каждой выборки. Если различие между выборками недостоверно, то результат должен быть близок к 1. Чем больше будет F по сравнению с 1, тем более досговерно различие.

302 Приложение Б

Таким образом, дисперсионный анализ показывает, принадлежат ли выборки к одной популяции, но с его помощью нельзя выделить те выборки, которые отличаются от других. Для того чтобы определить те пары выборок, разница между которыми достоверна, следует после дисперсионного анализа применить метод Шеффе. Поскольку, однако. этот весьма ценный метод требует достаточно больших вычислений. а к нашему гипотетическому эксперименту он неприменим, мы рекомен­дуем читателю для ознакомления с ним обратиться к какому-либо специальному пособию по статистике.

Непараметрические методыМетод /² («хи-квадрат»)

Для использования непараметрического метода у² не требуется вычислять среднюю или стандартное отклонение. Его преимущество состоит в том, что для применения его необходимо знать лишь зависи­мость распределения частот результатов от двух переменных; это позволяет выяснить, связаны они друг с другом или, наоборот, независи­мы. Таким образом, этот статистический метод используется для обра­ботки качественных данных (см. дополнение Б.1). Кроме того, с его помощью можно проверить, существует ли достоверное различие между числом людей, справляющихся или нет с заданиями какого-то интеллек­туального теста, и числом этих же людей, получающих при обучении высокие или низкие оценки; между числом больных, получивших новое лекарство, и числом тех, кому это лекарство помогло; и, наконец, существует ли достоверная связь между возрастом людей и их успехом или неудачей в выполнении тестов на память и т.п. Во всех подобных случаях этот тест позволяет определить число испытуемых, удовлетво­ряющих одному и тому же критерию для каждой из переменных.

При обработке данных нашего гипотетического эксперимента с по­мощью метода Стьюдента мы убедились в том, что употребление марихуаны испытуемыми из опытной группы снизило у них эффектив­ность выполнения задания по сравнению с контрольной группой. Одна­ко к такому же выводу можно было бы прийти с помощью другого метода-/². Для этого метода нет ограничений, свойственных методу Стьюдента: он может применяться и в тех случаях, когда распределение не является нормальным, а выборки невелики.

При использовании метода у² достаточно сравнить число испытуе­мых в той и другой группе, у которых снизилась результативность, и подсчитать, сколько среди них было получивших и не получивших наркотик; после этого проверяют, есть ли связь между этими двумя переменными.

Из результатов нашего опыта, приведенных в таблице в дополнении Б.2, видно, что из 30 испытуемых, составляющих опытную и контроль­ную группы, у 18 результативность снизилась, а 13 из них получили марихуану. Теперь надо внести значение этих так называемых эмпириче­ских частот (Э) в специальную таблицу:

Статистика и обработка данных 303