Как проверяют гипотезу о равенстве двух дисперсий?

Имеем 2 независимые выборки:

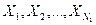(число измерений N₁, стандартное отклонение S₁)

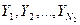(число измерений N₂, стандартное отклонение S₂)

Обе выборки получены из нормальных совокупностей со стандартным отклонением σ₁ и σ₂ соответственно.

H₀: ( 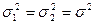): обе выборки из одной и той же нормальной совокупности с дисперсией σ²

Проверка с использованием F-критерия

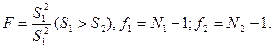
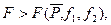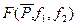Гипотеза H₀ отвергается при где - процентная точка.

На результаты проверки по этому критерию сильно влияют грубые промахи, поэтому сначала необходимо исследовать выборки на наличие подозрительно выделяющихся значений.F -критерий относится к параметрическим критериям.

1. Как проверяют гипотезу о равенстве двух математических ожиданий при несвязанных выборках?

Гипотеза о равенстве 2 математических ожиданий при независимых выборках (например, сравнение концентрации вещества в 2-х колбах, при исходном предположении, что в обеих колбах один и тот же раствор).

Использование t-критерия (Стьюдента):

Имеем 2 независимые выборки

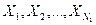(среднее значение , стандартное отклонение S_x ,число измерений N₁)

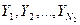( среднее значение , стандартное отклонение S_y ,число измерений N₂)

Обе выборки получены из нормальных совокупностей: первая с математическим ожиданием μ₁ и стандартным отклонением σ₁, вторая с μ₂, σ₂.

Н₀: , т.е. гипотеза о том. Что разница между , есть лишь следствие случайных погрешностей. Процедуру проверки гипотезы проводят в следующей последовательности:

1. Проверяем гипотезу о том, что обе выборки получены из нормальных совокупностей с одинаковой дисперсией H₀: ( 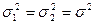) (с помощью критерия Фишера)

2.1. Если Н₀ не отвергается, то рассчитываем стандартное отклонение разности средних значений ( - ) сравниваемых выборок

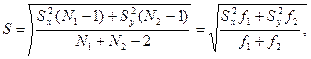где и 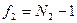-числа степеней свободы для рассматриваемых выборок.

Рассчитываем величину которая имеет t-распределение с степенями свободы

Вычисленную величину t сравнивают с процентной точкой t-распределения, соответствующей выбранной доверительной вероятности и числу степеней свободы . Если , то гипотезу Н₀: отвергают.

2.2. Если Н₀ отвергнута, то величину t рассчитывают по формуле . Эта величина имеет распределение, близкое к распределению Стьюдента с числом степеней свободы и дальше аналогично.

Возможна ситуация, когда у нас 1 выборка (среднее значение , стандартное отклонение S), полученная из нормальной совокупности с математическим ожиданием μ₁, и необходимо проверить гипотезу Н₀: 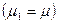, где μ-точно известная величина. Тогда величину t рассчитывают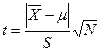

Следует отметить, что доверительная вероятность выбирают, учитывая какова альтернативная гипотеза. Если априорная информация о возможном соотношении μ₁ и μ₂ отсутствует, проводят проверку по двустороннему критерию, а если заведомо известно, что μ₁>μ₂ или μ₁<μ₂ – по одностороннему. В случае использования двухстороннего критерия выбирают ошибку I рода 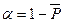в 2 раза меньшую, чем для одностороннего критерия.

Также можно воспользоваться Непараметрический критерий U(критерий Вилкоксона-Манна-Уитни)

1. Как проверяют гипотезу о равенстве двух математических ожиданий при связанных выборках?

Гипотеза о равенстве 2 мат ожиданий при связанных выборках (некоторый набор проб проанализирован 2 лабораториями, причем каждый лаборант произвел по 1 измерению каждой пробы). Для решения таких задач используют t-критерий и непараметрические методы.

Н₀ о том, что обе выборки из одной ген совокупности.

t-критерий. Имеем m пар взаимосвязанных результатов (Х_i;Y_i) где Х_i-результаты измерений из первой выборки, Y_i- результаты измерений из второй выборки. В нашем примере Х_i и Y_i- результаты измерений, полученные двумя лаборантами для одной и той же i-ой пробы.

Рассчитывают разности (d_i имеет нормальное распределение с мат ожиданием μ_d )

Далее проверяем 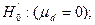это означает, что если основная гипотеза верна, разности d_i должны быть беспорядочно рассеяны вокруг нулевого значения, т.е. гипотезы H₀ и эквивалентны. Для проверки гипотезы рассчитывают величину . Если 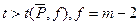гипотеза отвергается.

Критерий знаков. Находим для каждой пары (Х_i;Y_i) знак разности . Если обе связанные выборки получены из одной совокупности, вероятность появления знака + равна p=0,5. Таким образом необходимо проверить гипотезу 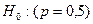. Подсчитываем число менее встречающихся знаков n и сравниваем его с критическим значением 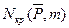. Гипотеза H₀ отвергается если 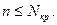Этот критерий хорошо работает когда много измерений. Если мало измерений, то существует парный критерий Вилкоксона. Для этого рассчитывают и располагают их по увеличению и по уменьшению и нумеруют (присваивают ранг). Считаем сумму рангов слева от нуля (в обоих рядах). Выбираем меньшее число Т и савниваем его с , где N-число пар (Х_i;Y_i) . Если 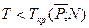, то отвергаем H₀.

1. Какие статистические методы позволяют ответить на вопрос, взаимозависимы ли две переменные?

1.Проверка взаимосвязи двух физических величин не представляет никакой трудности в случае, когда случайные погрешности малы, а диапазон, в котором лежат результаты измерений, достаточно широк. Тогда наличие или отсутствие связи и ее вид становятся очевидными если нанести точки X_i , Y_i на координатную плоскость. Во всех остальных случаях применяют количественные методы проверки основной гипотезы.

2.Простейшим из них является метод с использованием непараметрического критерия знаков. Этот метод выявляет только достаточно очевидную связь между двумя величинами.

3.В случае нормального распределения величин X и Y проверку гипотезы об отсутствии линейной зависимости вида между ними проводят с использованием выборочного коэффициента линейной корреляции r.

4.С использованием номограммы, на которой по осям нанесены выборочный коэффициент корреляции r и его истинное значение ρ, а на кривых, каждая из которых соответствует тому или иному объему выборки m, указаны доверительные интервалы для ρ, можно проводить графическую проверку гипотезы H₀ об отсутствии линейной зависимости между измеряемыми величинами. Если величина r (выборочный коэффициент корреляции) не попадает в доверительный интервал для истинного значения ρ, то гипотеза о независимости отвергается.

5.Непараметрический коэффициент корреляции рангов (коэффициент Спирмена) используется, если величины X и Y не имеют нормального распределения.