Конструктивные исчисления высказываний В. И. Гливенко и А. Н. Колмогорова

Первыми представителями конструктивной логики были на­ши отечественные математики — А. Н. Колмогоров (1903— 1987) и В. И. Гливенко (1897—1940). Первое исчисление, не соде­ржащее закона исключенного третьего, было предложено в 1925 г. А. Н. Колмогоровым в связи с его критикой концепции Л. Брауэра, а в дальнейшем развито В. И. Гливенко. Позже было опубликовано исчисление Гейтинга, которое Колмогоров интерпретировал как исчисление задач, что легло в основу содер­жательного истолкования исчислений, не пользующихся законом исключенного третьего, а это, в свою очередь, стало основой всех дальнейших, подлинно научных исследований таких исчислений.

С помощью введения понятий «псевдоистинность» (двойное отрицание суждения) и «псевдоматематика» («математика псев­доистинности») Колмогоров доказал, что всякий вывод, получен­ный с помощью закона исключенного третьего, верен, если вме­сто каждого суждения, входящего в его формулировку, поставить суждение, утверждающее его двойное отрицание. Тем самым он показал, что в «математике псевдоистинности» возможно приме­нение принципа исключенного третьего.

Колмогоров различает две логики суждений —общую и част­ную. Различие между ними в одной аксиоме А -> А, которая имеется лишь среди аксиом частной логики. Интересна взаимо­связь соотношения содержания и областей применения этих логик: содержание частной логики суждений богаче, чем обшей, так как частная логика дополнительно включает аксиому 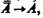но область применения ее уже. Из системы частной логики можно вывести все формулы традиционной логики суждений.

Какова же область применения частной логики суждений? Все ее формулы верны для суждений типа А', в том числе для всех финитных и для всех отрицательных суждений, т. е. область применимости ее совпадает с областью применимости формулы двойного отрицания (Символами А', В' ... обозначены произвольные суждения, для которых из двойного отрицания следует само суждение.)