Примеры метрических пространств
1. Пространство изолированных точек.
Произвольное множество 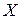 и
и 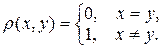
2. Множество действительных чисел с расстоянием 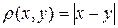 образует метрическое пространство
образует метрическое пространство 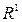 .
.
3. Множество упорядоченных групп из 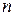 действительных чисел
действительных чисел 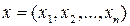 с
с 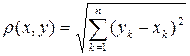 называется
называется 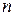 – мерным арифметическим евклидовым пространством
– мерным арифметическим евклидовым пространством 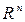 .
.
Доказательство.
Для того, чтобы доказать, что пространство является метрическим, необходимо проверить выполнимость аксиом.
Пусть 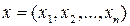 ,
,  ,
, 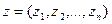 .
.
А1.  и
и 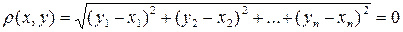
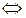
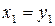 ,
,  , …,
, …, 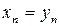 , т. е.
, т. е. 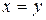 .
.
А2. 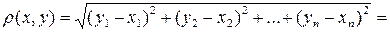
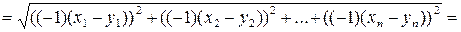
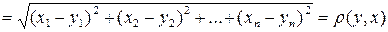 .
.
А3. Проверим, выполняется ли в 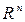 аксиома треугольника. Запишем аксиому в виде:
аксиома треугольника. Запишем аксиому в виде:
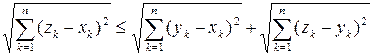 .
.
Полагая 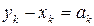 ,
, 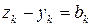 , получим
, получим 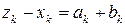 и
и 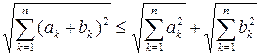 .
.
Для доказательства этого неравенства используется неравенство Коши–Буняковского 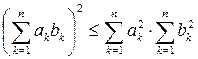 .
.
Действительно,
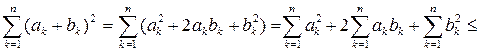
 ,
,
т.е. 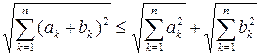 .
.
Следовательно, аксиома треугольника выполнена, и рассматриваемое множество с заданной метрикой является метрическим пространством.
Что и требовалось доказать.
4. Множество упорядоченных групп из 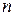 действительных чисел
действительных чисел 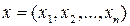 с
с 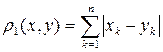 . Это метрическое пространство обозначается
. Это метрическое пространство обозначается 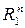 .
.
5. Множество упорядоченных групп из 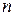 действительных чисел
действительных чисел 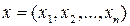 с
с  . Это метрическое пространство обозначается
. Это метрическое пространство обозначается  .
.
Примеры 3, 4 и 5 показывают, что один и тот же запас точек может быть по-разному метризован.
6. Множество 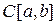 всех непрерывных действительных функций, определенных на сегменте
всех непрерывных действительных функций, определенных на сегменте 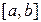 с расстоянием
с расстоянием 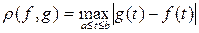 . Обозначают это метрическое пространство как и само множество точек пространства:
. Обозначают это метрическое пространство как и само множество точек пространства: 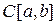 . В частности, вместо
. В частности, вместо 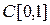 пишут
пишут 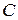 .
.
7. Через 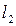 обозначается метрическое пространство, точками которого служат всевозможные последовательности
обозначается метрическое пространство, точками которого служат всевозможные последовательности 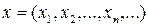 действительных чисел, удовлетворяющие условию
действительных чисел, удовлетворяющие условию 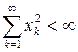 , и метрика определяется формулой
, и метрика определяется формулой 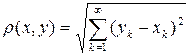 .
.
Доказательство.
Так как 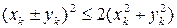 , то
, то 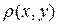 имеет смысл при всех
имеет смысл при всех  . Т.е. ряд
. Т.е. ряд 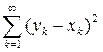 сходится, если
сходится, если 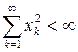 и
и 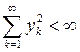 .
.
Покажем, что 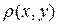 удовлетворяет аксиомам.
удовлетворяет аксиомам.
Аксиомы 1, 2 очевидны. Аксиома треугольника примет вид:
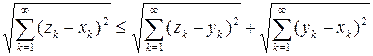 .
.
Все ряды являются сходящимися.
Неравенство справедливо для любого 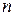 (см. пример 3). При
(см. пример 3). При 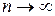 получаем неравенство для
получаем неравенство для 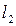 .
.
Что и требовалось доказать.
8. Рассмотрим совокупность всех функций, непрерывных на отрезке 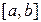 и
и  . Такое метрическое пространство обозначается
. Такое метрическое пространство обозначается 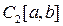 и называется пространством непрерывных функций с квадратичной метрикой.
и называется пространством непрерывных функций с квадратичной метрикой.
9. Рассмотрим множество всех ограниченных последовательностей 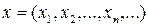 действительных чисел. Определим
действительных чисел. Определим 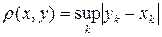 . Это метрическое пространство обозначается
. Это метрическое пространство обозначается  .
.
10. Множество упорядоченных групп из 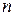 действительных чисел с расстоянием
действительных чисел с расстоянием 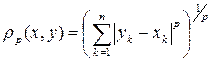 , где
, где 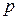 – любое фиксированное число
– любое фиксированное число 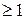 , представляет собой метрическое пространство, обозначаемое
, представляет собой метрическое пространство, обозначаемое 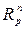 .
.
Рассмотренная в этом примере метрика 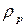 превращается в евклидову метрику при
превращается в евклидову метрику при 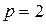 (см. пример 3) и в метрику примера 4 при
(см. пример 3) и в метрику примера 4 при 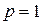 . Можно показать, что метрика
. Можно показать, что метрика  (см. пример 5) является предельным случаем
(см. пример 5) является предельным случаем 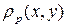 .
.
11. Рассмотрим всевозможные последовательности 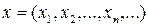 действительных чисел, удовлетворяющие условию
действительных чисел, удовлетворяющие условию 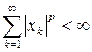 , где
, где 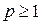 – некоторое фиксированное число, а расстояние определяется формулой
– некоторое фиксированное число, а расстояние определяется формулой 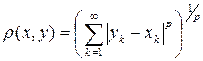 . Имеем метрическое пространство
. Имеем метрическое пространство 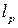 .
.
12. Пусть 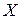 – множество всех бесконечных последовательностей –комплексных чисел
– множество всех бесконечных последовательностей –комплексных чисел 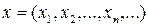 . Определим
. Определим 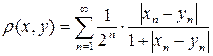 . Имеем метрическое пространство.
. Имеем метрическое пространство.
Определение: Пусть 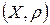 – метрическое пространство и
– метрическое пространство и 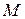 – любое подмножество
– любое подмножество 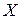 . Тогда
. Тогда 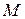 с той же функцией
с той же функцией 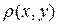 , которая теперь определена для
, которая теперь определена для 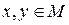 , представляет собой метрическое пространство, которое называется подпространством пространства
, представляет собой метрическое пространство, которое называется подпространством пространства 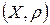 .
.
Основные понятия
Обозначим метрическое пространство 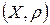 через
через  .
.
Определение: Последовательность 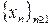 , принадлежащая метрическому пространству, называется фундаментальной, если каждому
, принадлежащая метрическому пространству, называется фундаментальной, если каждому 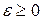 соответствует номер
соответствует номер 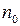 такой, что для любых
такой, что для любых  справедливо неравенство
справедливо неравенство 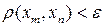 .
.
Определение: Последовательность 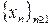 , принадлежащая метрическому пространству
, принадлежащая метрическому пространству  , называется сходящейся, если существует
, называется сходящейся, если существует  такой, что каждому
такой, что каждому 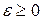 соответствует номер
соответствует номер 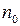 такой, что для всех
такой, что для всех 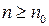 справедливо неравенство
справедливо неравенство 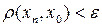 . Тогда
. Тогда  называется пределом последовательности.
называется пределом последовательности.
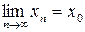
Теорема: Если последовательность имеет предел, то он единственный.
Доказательство.
Действительно, если 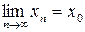 и
и 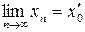 , то
, то 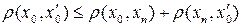 . Так как
. Так как 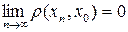 и
и 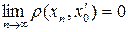 , то
, то 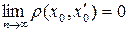 , т.е.
, т.е. 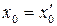 .
.
Теорема доказана.
Определение: Полным метрическим пространством называется метрическое пространство, в котором каждая фундаментальная последовательность сходится.
Теорема: Метрика как функция двух аргументов является непрерывной функцией, т.е. если 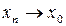 и
и 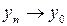 , то
, то 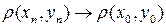 .
.
Доказательство:
Пусть 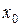 ,
,  ,
, 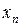 ,
, 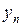
 .
.
По неравенству треугольника:
 (1)
(1)
и
 . (2)
. (2)
Из (1) получаем:
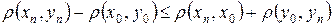 .
.
Из (2) получаем:
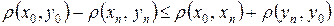 .
.



 .
.
Так как 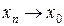

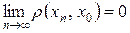 ,
,
так как 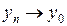

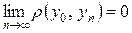

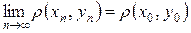
ч.т.д.
Обозначим  .
.
В метрическом пространстве  можно рассматривать различные множества, окрестности точек, предельные точки и другие понятия классического анализа.
можно рассматривать различные множества, окрестности точек, предельные точки и другие понятия классического анализа.
Определение: Под окрестностью точки  понимают множество, содержащие открытый шар радиуса
понимают множество, содержащие открытый шар радиуса  с центром в точке
с центром в точке 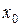 , т.е.
, т.е.
 .
.
Определение: Точка 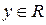 называется предельной точкой для множества
называется предельной точкой для множества 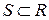 , если в любой окрестности точки
, если в любой окрестности точки  содержится хотя бы одна точка из
содержится хотя бы одна точка из 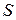 , отличная от
, отличная от  .
.
Определение: Точка 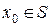 называется внутренней точкой множества
называется внутренней точкой множества 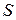 , если она входит в
, если она входит в 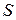 вместе с некоторой своей окрестностью
вместе с некоторой своей окрестностью  .
.
Определение: Множество 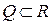 называется открытым, если оно состоит из одних внутренних точек. Множество
называется открытым, если оно состоит из одних внутренних точек. Множество 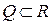 называется замкнутым в себе, если оно содержит все свои предельные точки.
называется замкнутым в себе, если оно содержит все свои предельные точки.
Метрическое пространство является замкнутым.
Подпространства 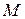 могут быть и не замкнутыми подмножествами
могут быть и не замкнутыми подмножествами  .
.
Если к 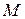 присоединить все его предельные точки, то получаем замыкание
присоединить все его предельные точки, то получаем замыкание 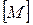 .
.
Определение: Множество 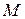 , лежащее в метрическом пространстве
, лежащее в метрическом пространстве  называется замкнутым, если оно совпадает со своим замыканием:
называется замкнутым, если оно совпадает со своим замыканием: 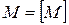 .
.
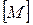 - замкнутое множество, есть наименьшее замкнутое множество, содержащие
- замкнутое множество, есть наименьшее замкнутое множество, содержащие 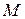 .
.
Определение: Пусть 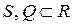 . Множество
. Множество 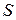 называется плотным в
называется плотным в 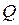 , если
, если  . Множество
. Множество 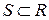 называется всюду плотным, если
называется всюду плотным, если 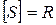 . Множество
. Множество 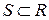 называется нигде не плотным в
называется нигде не плотным в  , если каков бы ни был шар
, если каков бы ни был шар  , найдется другой шар
, найдется другой шар 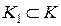 , свободный от точек множества
, свободный от точек множества 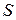 .
.
Определение: Пространство  называется сепарабельным, если в нем существует всюду плотное счетное множество.
называется сепарабельным, если в нем существует всюду плотное счетное множество.
В математическом анализе важную роль играет свойство полноты числовой прямой, то есть тот факт, что всякая фундаментальная последовательность действительных чисел сходится к некоторому пределу (Критерий сходимости Коши).
Числовая прямая служит примером полным метрических пространств.
Пространства изолированных точек,  ,
, 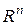 ,
, 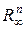 ,
,  ,
, 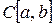 ,
, 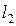 являются полными метрическими пространствами.
являются полными метрическими пространствами.
Пространство 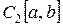 не полно.
не полно.
В анализе широко используется так называемая лемма о вложенных отрезках:
Пусть 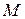 - система вложенных отрезков. Тогда
- система вложенных отрезков. Тогда  для
для 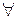 отрезка
отрезка 
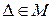 имеем
имеем 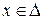 .
.
Это значит, что все отрезки 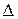 из множества
из множества 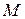 имеют общую точку
имеют общую точку 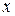 .
.
В теории метрических пространств аналогичную роль играет теорема о вложенных шарах.
Теорема: Для того, чтобы метрическое пространство  было полным необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга шаров, радиусы которых
было полным необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга шаров, радиусы которых  , имела непустое пересечение.
, имела непустое пересечение.
Доказательство:
Необходимость:
Пусть  - полное метрическое пространство и пусть
- полное метрическое пространство и пусть 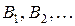 - последовательность вложенных друг в друга замкнутых шаров.
- последовательность вложенных друг в друга замкнутых шаров.
Пусть  - радиус, а
- радиус, а 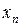 - центр шара
- центр шара  .
.
Последовательность центров 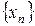 - фундаментальна, так как
- фундаментальна, так как 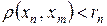 при
при 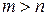 , а
, а 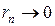 при
при 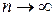 . Так как
. Так как  - полно, то
- полно, то 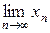
 . Положим
. Положим 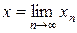 , тогда
, тогда 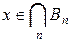 . Действительно, шар
. Действительно, шар  содержит все точки последовательности
содержит все точки последовательности 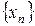 , за исключением, быть может точек
, за исключением, быть может точек 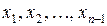 . Таким образом точка
. Таким образом точка 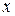 является точкой прикосновения (предельной точкой) для каждого шара
является точкой прикосновения (предельной точкой) для каждого шара  . Но так как
. Но так как  - замкнутое множество, то
- замкнутое множество, то 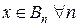 .
.
Достаточность:
Пусть 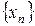 - фундаментальная последовательность. Докажем, что она имеет предел. В силу фундаментальности можем выбрать такую точку
- фундаментальная последовательность. Докажем, что она имеет предел. В силу фундаментальности можем выбрать такую точку 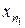 последовательности, что
последовательности, что 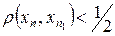 при всех
при всех 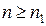 . Примем точку
. Примем точку 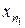 за центр замкнутого шара радиуса
за центр замкнутого шара радиуса 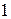 .Обозначим этот шар
.Обозначим этот шар  .
.
Выберем затем  из
из 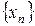 так, чтобы любой
так, чтобы любой 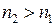
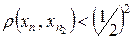 при любом
при любом  . Примем точку
. Примем точку  за центр шара радиуса
за центр шара радиуса 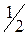 и обозначим этот шар
и обозначим этот шар  .
.
Если 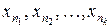 уже выбраны
уже выбраны  , то выберем
, то выберем 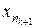 так, чтобы
так, чтобы 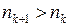 и
и 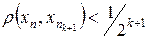 при всех
при всех 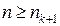 и окружим его замкнутым шаров
и окружим его замкнутым шаров 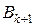 радиуса
радиуса 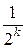 . Продолжая это построение, получим последовательность шаров
. Продолжая это построение, получим последовательность шаров 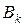 , вложенных друг в друга, причем шар
, вложенных друг в друга, причем шар 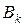 имеет радиус
имеет радиус  . Эта последовательность шаров имеет, по предположению, общую точку, обозначим её
. Эта последовательность шаров имеет, по предположению, общую точку, обозначим её 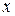 .
.
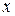 служит пределом последовательности
служит пределом последовательности 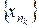 . Но если фундаментальная последовательность содержит сходящуюся к
. Но если фундаментальная последовательность содержит сходящуюся к 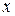 подпоследовательность, то она сама сходится к тому же пределу, таким образом
подпоследовательность, то она сама сходится к тому же пределу, таким образом  .
.
ч.т.д.
Теорема (Бэр): Полное метрическое пространство  не может быть представлено в виде объединения счетного числа нигде не плотных множеств.
не может быть представлено в виде объединения счетного числа нигде не плотных множеств.
Доказательство:
Докажем от противного.
Пусть  , где каждое из
, где каждое из  нигде не плотно. Пусть
нигде не плотно. Пусть 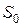 - некоторый замкнутый шар радиуса
- некоторый замкнутый шар радиуса 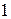 . Поскольку множество
. Поскольку множество 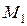 , будучи нигде не плотным, не плотно в
, будучи нигде не плотным, не плотно в 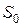 , существует замкнутый шар
, существует замкнутый шар 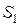 радиуса
радиуса 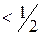 , такой, что
, такой, что 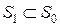 и
и 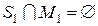 .
.
Так как 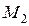 не плотно в
не плотно в 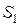 , то в
, то в 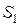 содержится замкнутый шар
содержится замкнутый шар 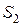 радиуса
радиуса 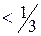
 и т.д.
и т.д.
Получаем последовательность вложенных друг в друга замкнутых шаров 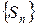 , радиусы которых
, радиусы которых  , причем
, причем  . В силу теоремы о вложенных шарах пересечение
. В силу теоремы о вложенных шарах пересечение 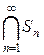 содержит некоторую точку
содержит некоторую точку 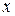 , которая по построению не принадлежит ни одному из множеств
, которая по построению не принадлежит ни одному из множеств  и
и 
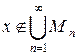 , то есть
, то есть 
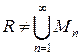
 противоречие, ч.т.д
противоречие, ч.т.д
В частности, всякое полное метрическое пространство без изолированных точек несчетно.
Действительно, в таком пространстве каждое множество, содержащее лишь одну точку, нигде не плотно.
Если пространство  не полно, то его всегда можно включить некоторым единственным способом в полное пространство.
не полно, то его всегда можно включить некоторым единственным способом в полное пространство.
Определение: Пусть  - метрическое пространство. Полное метрическое пространство
- метрическое пространство. Полное метрическое пространство 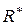 называется пополнением пространства
называется пополнением пространства  , если:
, если:
1)  является подпространством пространства
является подпространством пространства 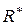 ,
,
2)  всюду плотно в
всюду плотно в 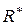 , то есть
, то есть 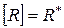 .
.
Например, пространство всех действительных чисел является пополнением пространства рациональных чисел.
Теорема: Каждое метрическое пространство  имеет пополнение, и это пополнение единственно с точностью до изометрии, оставляющей неподвижными точки из
имеет пополнение, и это пополнение единственно с точностью до изометрии, оставляющей неподвижными точки из  .
.
Дата добавления: 2014-12-08; просмотров: 9083;
