Законах материального мира

Первый тип моделей основан на фундаментальных законах материального мира (законы сохранения энергии, массы, количества движения, переноса, трансформации и др.). Исследователь проводит отбор наиболее существенных законов для конкретного объекта, осуществляет их формализованную запись, решает записанные уравнения и производит интерпретацию получаемых решений. К этому перечню зачастую добавляется процесс верификации моделей.

Подобные модели содержат в себе информацию как априорную, заключенную в структуре математической модели (тип дифференциального, интегрального, разностного, балансового или другого уравнения), так и информацию, содержащуюся в параметрах (коэффициентах) модели, которые определяются из опытных данных. Необходимо отметить, что и при отсутствии натурных данных о коэффициентах исследование решений математических уравнений модели позволит получить качественные, прогностические результаты.

Математическая модель пространственной турбулентной диффузии примесей в атмосфере или водной среде может представлять собой дифференциальное уравнение в следующем виде:

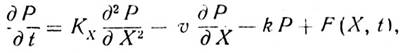
где t – время;

X – координата;

Р – концентрация примеси в объеме среды;

К_Х – коэффициент одномерной продольной диффузии, который численно равен потоку вещества, обусловленному диффузией при единичном градиенте концентрации;

υ – средняя скорость потока в среде;

k – коэффициент неконсервативности примеси (коэффициент, определяющий изменение концентрации примеси в среде за счет физико-химических превращений примеси; коэффициент самоочищения среды);

F(X, t) – пространственно-временная функция, характеризующая пространственное расположение источника загрязнения.

Напомним, что диффузией называется процесс выравнивания концентраций веществ в различных областях термодинамически однородной среды. В случае, когда диффузия обусловлена хаотическим движением молекул, она называется молекулярной, а в случае, когда диффузия обусловлена вихревыми потоками в жидкостях или газах – турбулентной.

Отметим, что данное уравнение может усложняться за счет многомерности, многофакторности, разнообразия граничных и начальных условий, специфики среды, примесей и других факторов. А его упрощение достигается, например, при возможности неучета функции источника примеси (F=0) или стационарности процесса поступления примеси в среду, т. е. δυ/δt=0, F(X, t)=F (X) при постоянстве скорости или коэффициента обмена К_Х. Отметим, что рост коэффициента К_Х означает замедление обмена, т. е. вредные примеси будут стремиться к накоплению, и при превышении норм самоочищения будет наблюдаться процесс дегенерации среды.

Математическая модель закономерностей формирования кислорода в придонном слое внутреннего водоема может представлять собой дифференциальное уравнение в таком виде (предполагается, что поступление кислорода из вышележащих слоев в придонный слой происходит с постоянной скоростью):

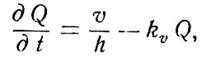
где Q - концентрация растворенного кислорода в придонном слое;

δQ/δt - скорость изменения содержания кислорода в придонном слое;

υ - скорость поступления кислорода в придонный слой;

h - толщина придонного слоя;

k_υ - коэффициент биохимического потребления кислорода водой и осадками.

Решение этого уравнения относительно величины υ представимо в виде следующего выражения:

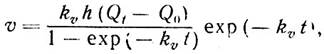
где Q₀ и Q_t - концентрация растворенного кислорода придонного слоя в начальный и конечный момент вертикального водообмена.

Зная или задаваясь значениями k_υ и h, контролируя датчиками содержание кислорода Q₀ и Q_t можно определять величину υ. При прогнозировании динамики величины υ можно варьировать значения как k_υ и h, так и Q₀ и Q_t

Решая задачу прогнозирования минерализации внутренних водоемов на основании уравнений солевого и водного баланса, можно получить упрощенную расчетную формулу ожидаемой средней минерализации воды

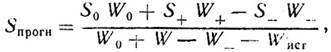
где S₀, S₊, S_- – средние значения минерализации водоема в начале расчетного периода, притоковых и стоковых вод;

W₀, W₊, W_- – объем водоема в начале расчетного периода, объем притоковых и стоковых вод;

W_исп – потери воды на испарение с поверхности водоема за расчетный период.

Трудности первого типа моделирования заключаются, с одной стороны, в неадекватности упрощенной модели ее реальному образу, а с другой стороны, в сложности обозримого представления реального образа многопараметрической моделью. К этим затруднениям присовокупляется влияние в реальной экологической ситуации случайных трудноучитываемых факторов, что делает головоломным формирование правдоподобных гипотез.