Материалов
Требуется выполнить лабораторные работы:
Лабораторная работа 2.1. Определение механических свойств и характеристик материалов при растяжении (экспериментальное построение диаграммы растяжения стали с определением ее механических характеристик, в том числе переменных параметров пластичности).
Лабораторная работа 2.2. Определение упругих постоянных материалов (экспериментальное определение упругих постоянных стального образца).
Лабораторная работа 2.3. Испытание материалов на сдвиг (экспериментальное определение предела прочности при сдвиге).
Лабораторная работа 2.4. Испытание на кручение бруса круглого поперечного сечения (экспериментальное определение модуля сдвига).
Задание 3. Определение перемещений в балках и стержневых системах энергетическим методом с использованием формулы Мора
Задача 3.1. Для балки из задачи 1.1 (рис. 6) определить прогиб в т. В и угол поворота сечения в т. С с помощью формулы Мора, используя способ Верещагина для вычисления ее интегралов.
Задача 3.2. Аудиторная самостоятельная контрольная работа.
Для балки из задачи 1.2 (рис. 7) определить прогиб в т. В и угол поворота сечения в т. С с помощью формулы Мора, используя способ Верещагина для вычисления ее интегралов.
Задача 3.3. Для рамы с постоянной жесткостью участков (EJX=const), (рис. 8) определить вертикальное и горизонтальное перемещение т. В.
Задание 4. Расчет статически неопределимых
балок методом сил
Задача 4.1. Аудиторная самостоятельная контрольная работа.
Для балки (рис. 9) с постоянной жесткостью участков (EJX=const) требуется:
1. Раскрыть статическую неопределимость.
2. Провести деформационную проверку правильности полученного решения.
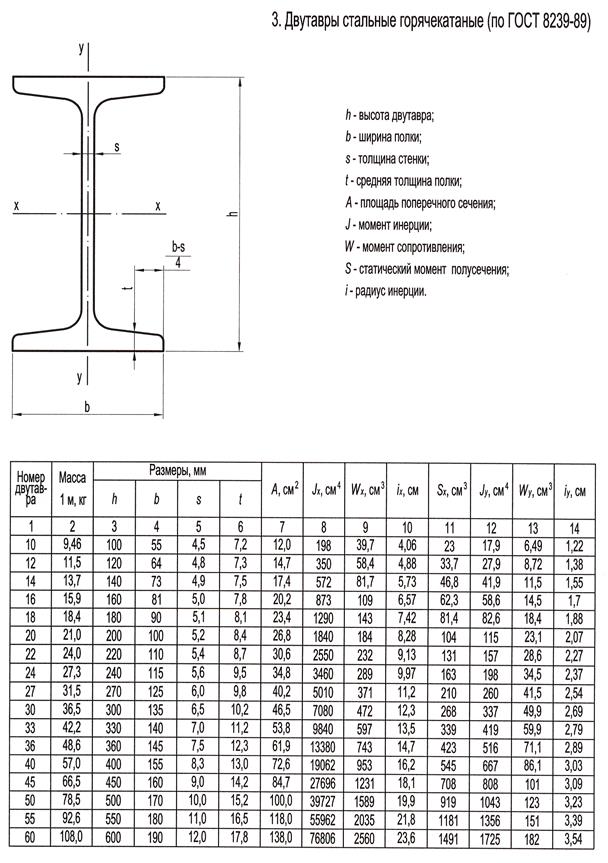
3. Подобрать двутавровое поперечное сечение, если [σ]=210 МПа.
Задача 4.2. Для балки (рис. 10) с постоянной жесткостью участков (EJX=const) требуется:
1. Раскрыть статическую неопределимость методом сил с рациональным выбором основной системы.
2. Провести деформационную проверку правильности полученного решения.
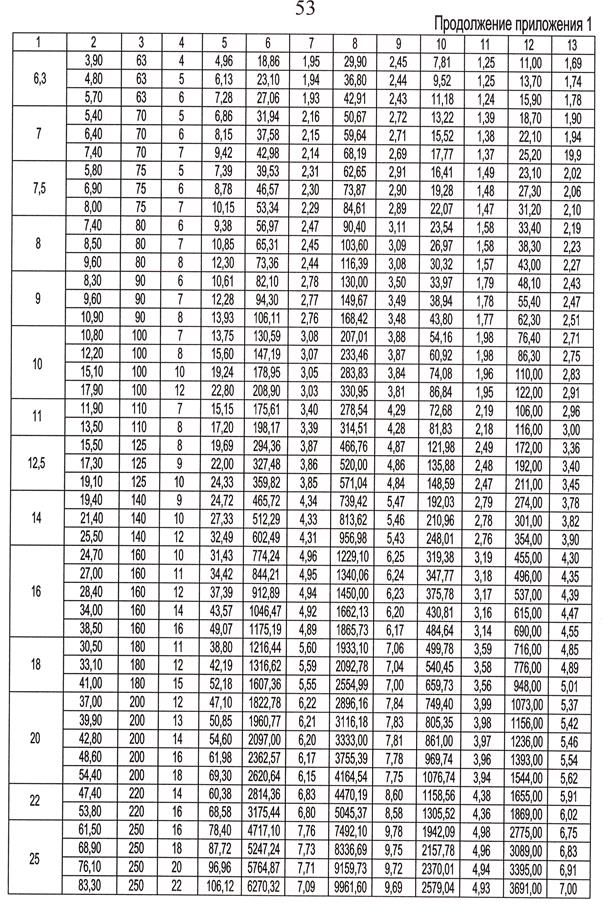
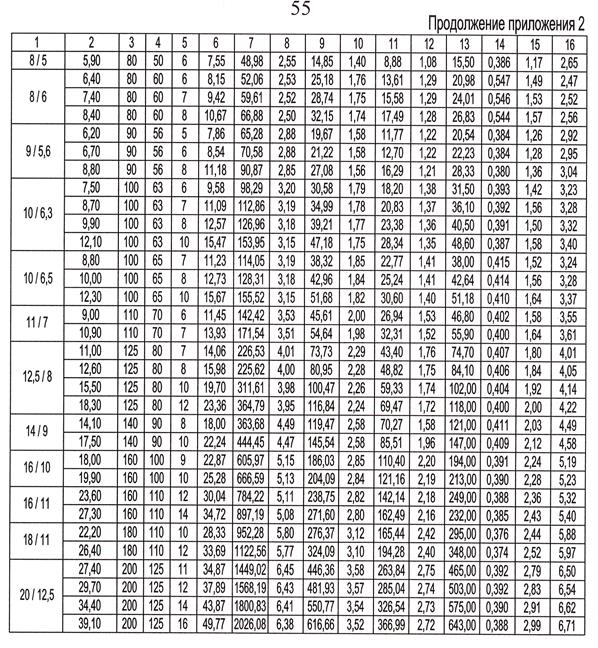
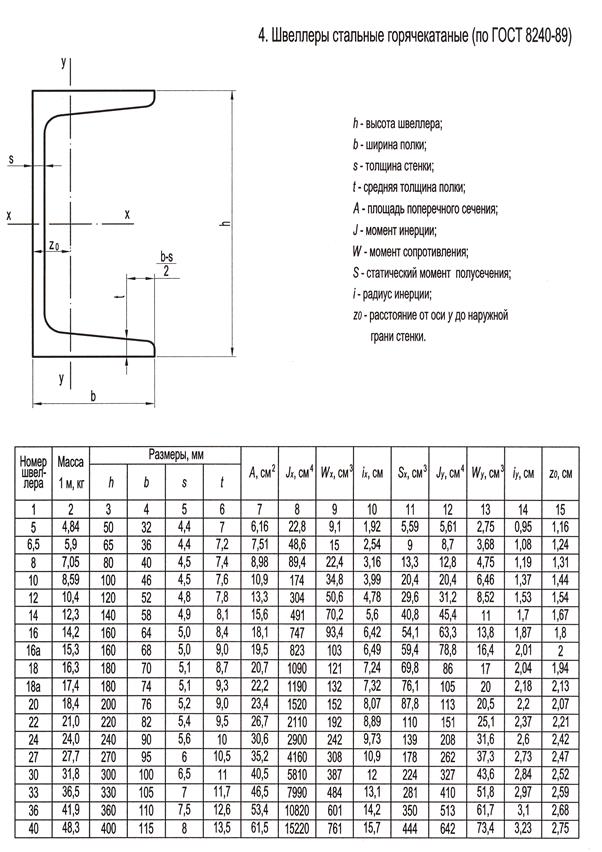
3. Подобрать поперечное сечение балки в виде двух швеллеров, если [σ]=210МПа.
4. Определить угол поворота сечения на одной из опор, приняв
E=2∙105 МПа.
Задание 5. Устойчивость упругих систем
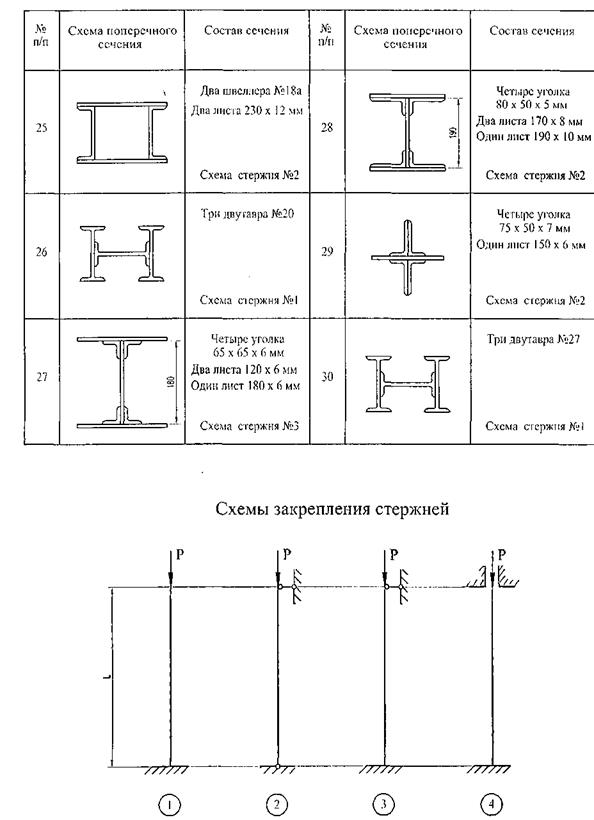
Задача 5.1. Определить допускаемую сжимающую силу Р на стальной стержень, поперечное сечение и схема закрепления которого приведены на рис.11. При решении использовать таблицу значений коэффициента снижения допускаемого напряжения на сжатие φ для стали Ст.3 (табл. 4). Основное допускаемое напряжение принять [σ]=160 МПа.
Таблица 4
Значения коэффициента φ
| № | Λ | Сталь Ст.3 | Сплав Д16Т | № | Λ | Сталь Ст.3 | Сплав Д16Т |
| 1,00 | 1,00 | 0,52 | 0,14 | ||||
| 0,99 | 1,00 | 0,45 | 0,12 | ||||
| 0,97 | 1,00 | 0,40 | 0,10 | ||||
| 0,95 | 0,84 | 0,36 | 0,087 | ||||
| 0,92 | 0,70 | 0,32 | 0,076 | ||||
| 0,89 | 0,57 | 0,29 | — | ||||
| 0,86 | 0,46 | 0,26 | — | ||||
| 0,81 | 0,35 | 0,23 | — | ||||
| 0,75 | 0,27 | 0,21 | — | ||||
| 0,69 | 0,21 | 0,19 | — | ||||
| 0,60 | 0,17 |
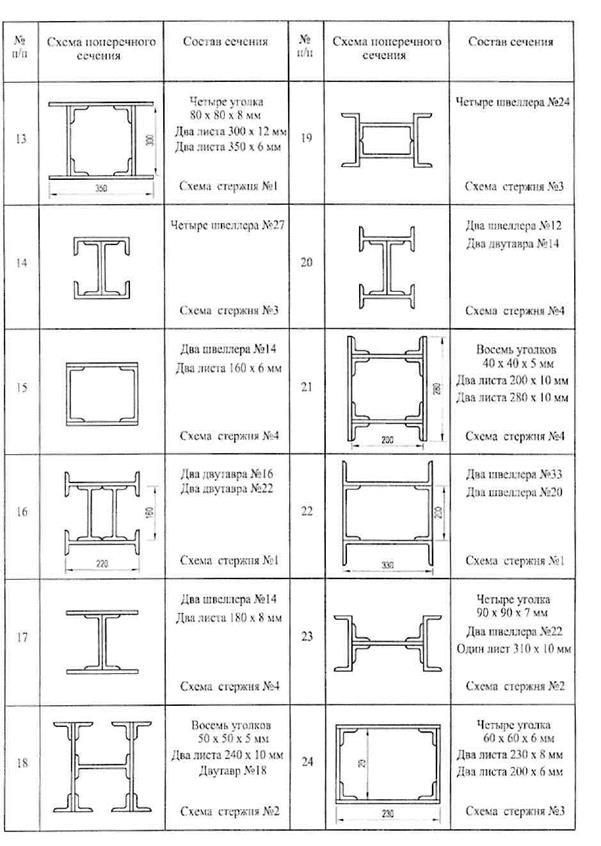
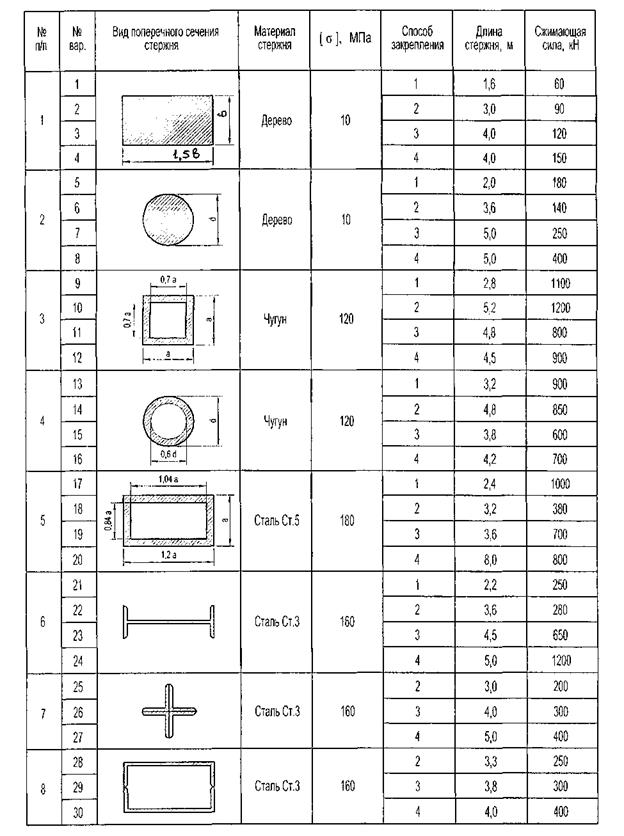
Задача 5.2. Для сжатого силой Р стального стержня длиной L и заданной формы поперечного сечения (рис. 12) подобрать в соответствии с методом Ф.С.Ясинского размеры данного сечения. Способы закрепления стержня приведены на рис. 11.
Эмпирические формулы Ф.С. Ясинского
σКР= a – bΛ при Λ0≤Λ≤Λ*,
σКР= σ0 при 0≤ Λ≤Λ0,
и Джонсона
σКР= σ0 – (σ0 – σПЦ)(Λ/Λ*)2 при Λ≤Λ*,
где 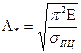 .
.
Принять для стали Ст.3 σПЦ=200 МПа, σ0=σТ=240 МПа, E=2∙105 МПа, Λ0=ΛТ=30; для сплава Д16Т – σПЦ=200 МПа, σТ=312 МПа, E=0,75∙105 МПа
σ0=σВ=364 МПа, Λ0=0.
Задание 6. Расчеты на прочность
при сложном напряженном состоянии
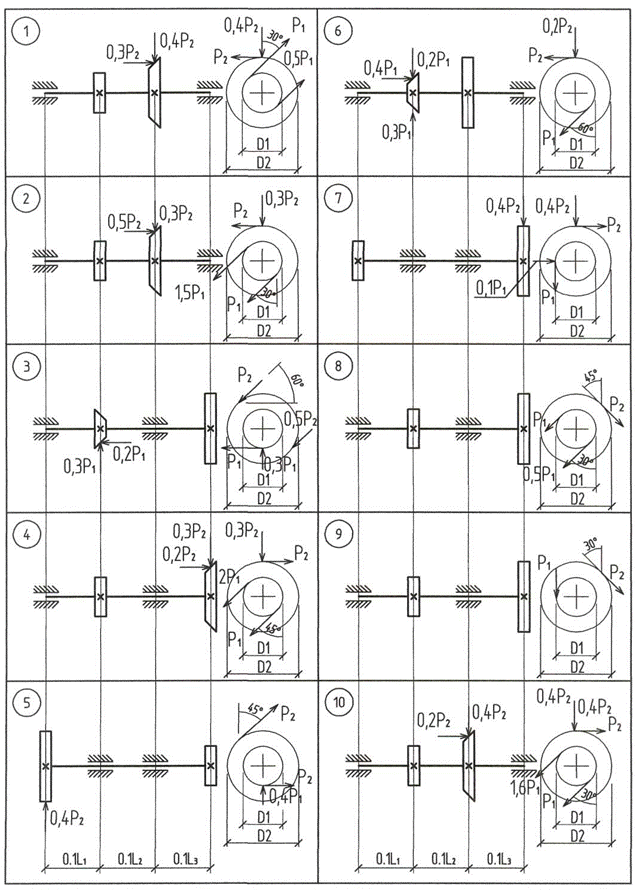
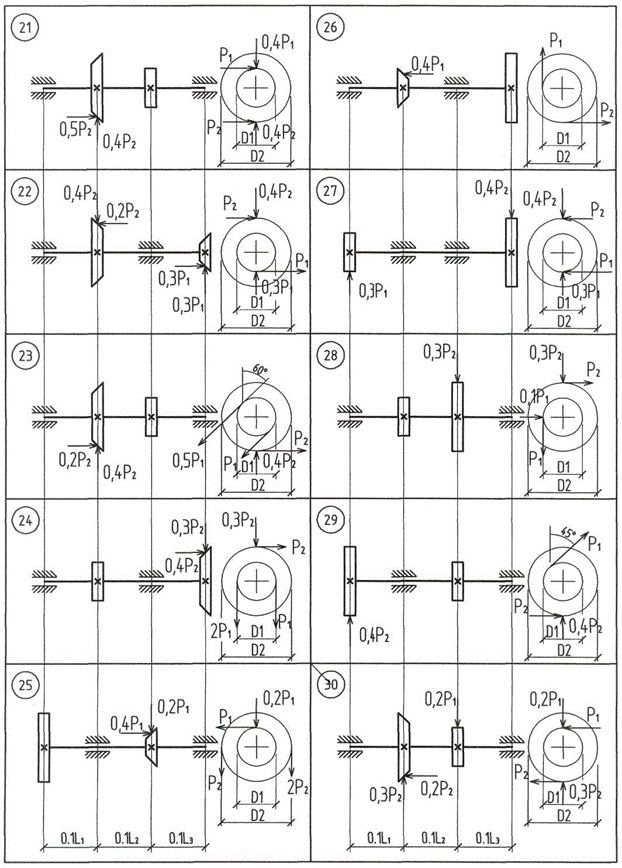
Задача 6.1. Для вала (рис. 13), изготовленного из стали 45, требуется:
1. Определить крутящий момент на валу по заданной мощности и числу оборотов.
2. Определить окружные, осевые и радиальные усилия, действующие на вал, если D1= м, D2= м.
3. Построить эпюру крутящего момента.
4. Построить эпюры изгибающих моментов от горизонтальных и вертикальных сил.
5. Построить эпюру суммарного изгибающего момента.
6. При помощи эпюр крутящего и суммарного изгибающего моментов найти и вычертить опасное сечение вала, указав на нем опасные точки (частицы).
7. Изобразить напряженное состояние в опасной точке (частице).
8. Подобрать диаметр вала из условий прочности Сен-Венана и Мизеса.
Задание 7. Экспериментальные основы исследования
напряженно-деформированного состояния
элементов конструкций
Требуется выполнить лабораторные работы:
Лабораторная работа 7.1. Определение перемещений в балках при поперечном изгибе (определение прогиба в длинной и короткой балках при изгибе).
Лабораторная работа 7.2. Определение перемещений при косом изгибе (экспериментальная проверка формулы для определения перемещений).
Лабораторная работа 7.3. Статически неопределимая балка (экспериментальное определение опорной реакции неразрезной балки).
Лабораторная работа 7.4. Устойчивость сжатого стержня (экспериментальное изучение явления потери устойчивости стержня при осевом сжатии).
Лабораторная работа 7.5. Концентрация напряжений в полосе с отверстием (экспериментальное определение коэффициента концентрации напряжений у края отверстия).
Лабораторная работа 7.6. Исследование напряженного состояния, возникающего в трубе при изгибе с кручением (экспериментальная проверка теоретических формул для расчета главных напряжений и положения главных площадок).
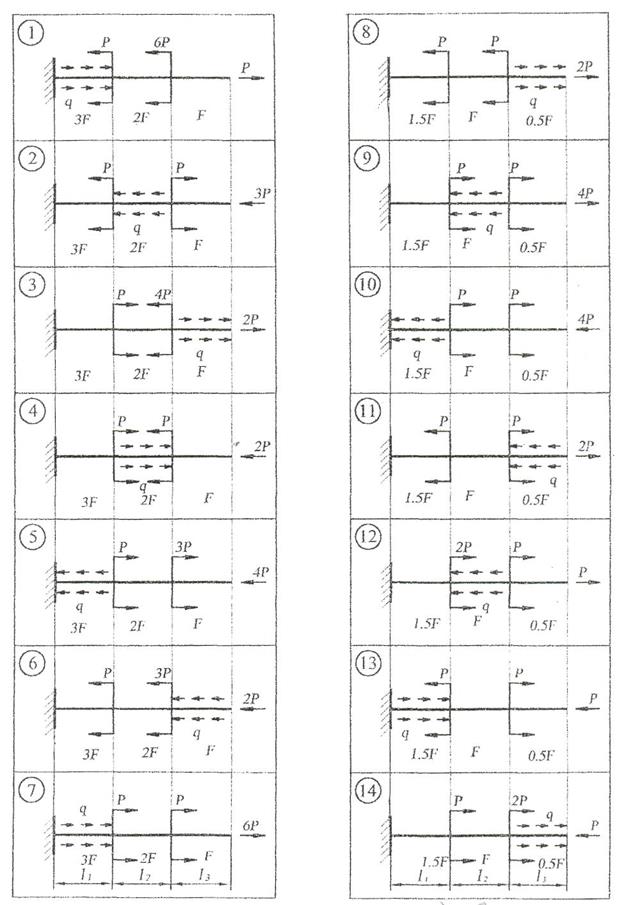
Рис. 1. Схемы к задаче 1.1

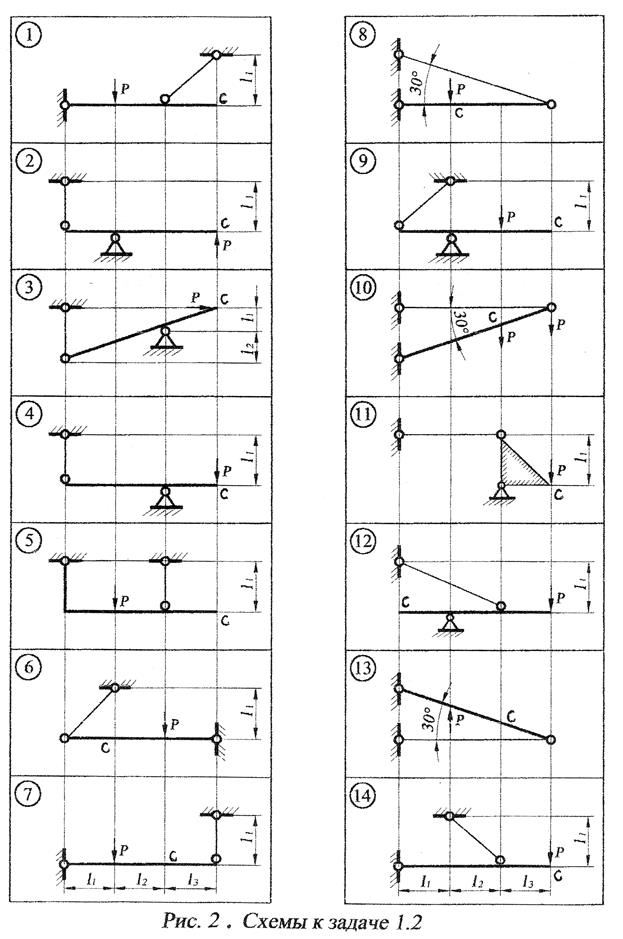
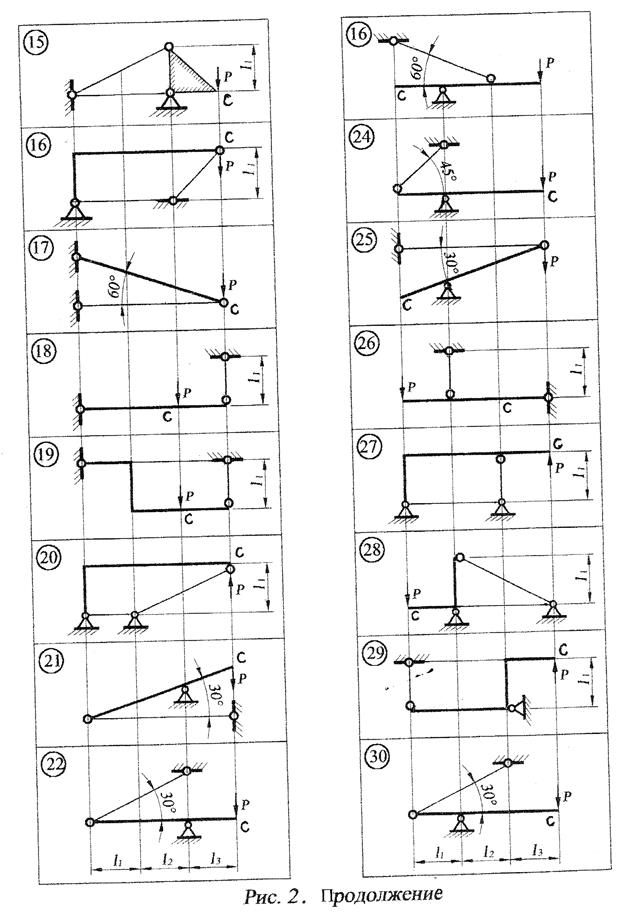
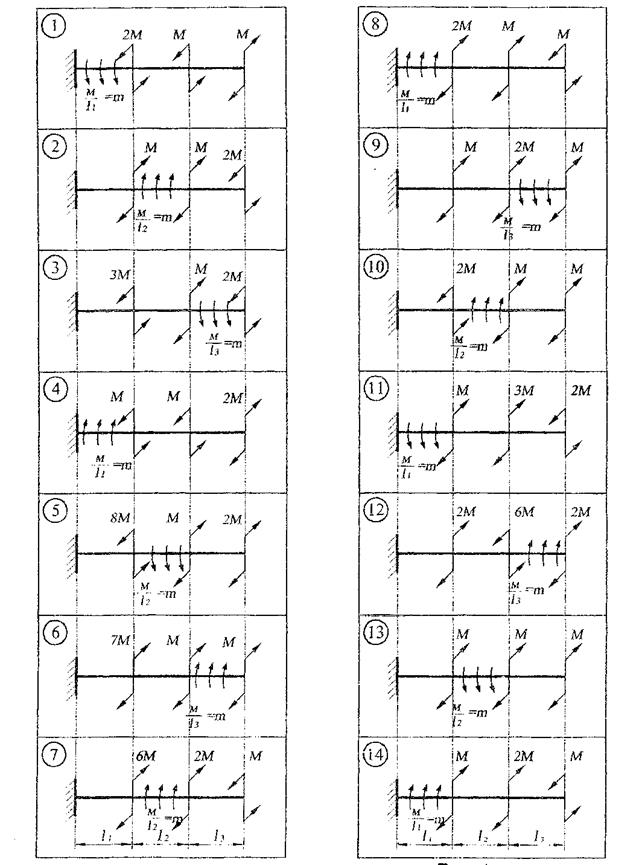
Рис. 3. Схемы к задаче 1.3
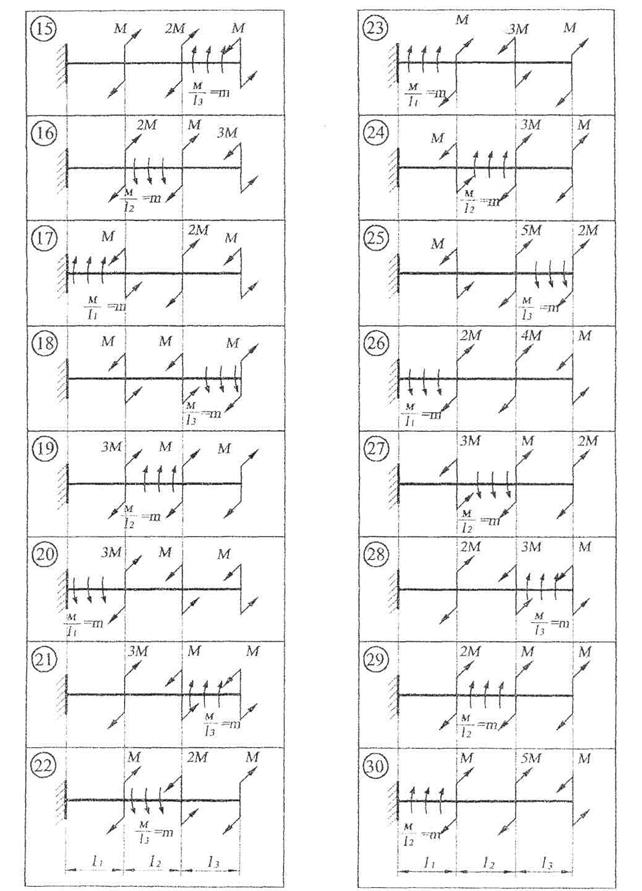
Рис. 3. Продолжение
|
Рис. 4. Схемы к задаче 1.4
|
Рис. 4. Продолжение

|
Рис. 5. Схемы к задаче 1.5

|
Рис. 5. Продолжение
|
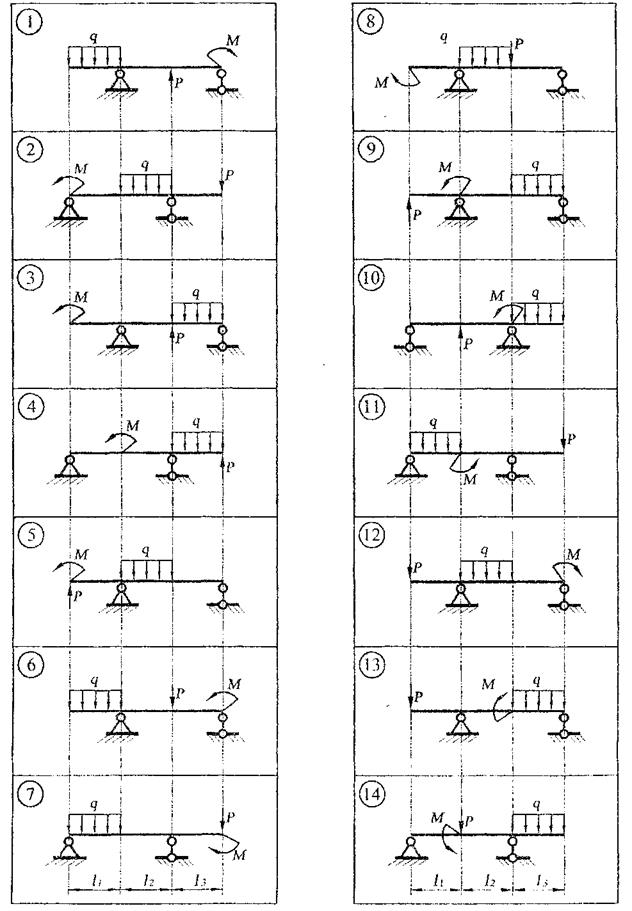
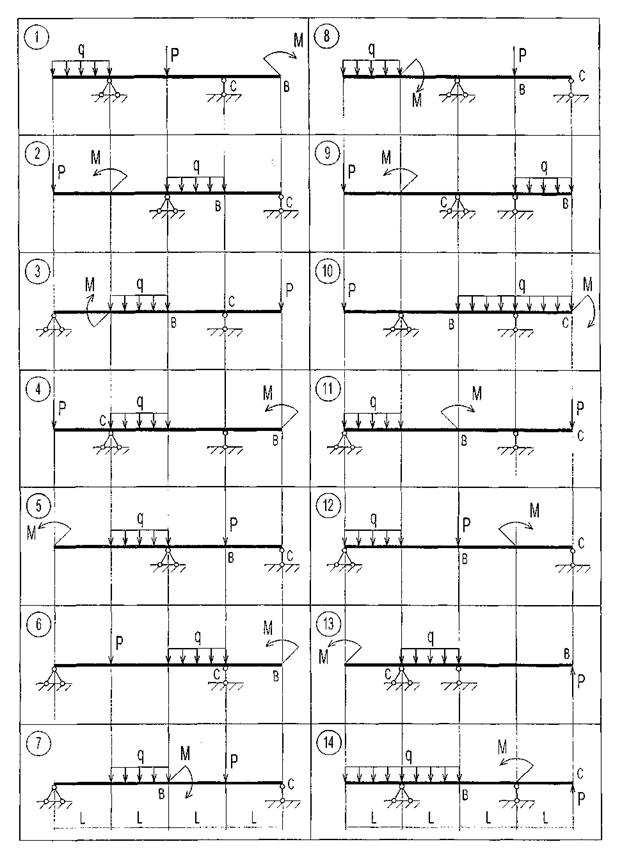
Рис. 6. Схемы к задаче 3.1
|
Рис. 6. Продолжение

|
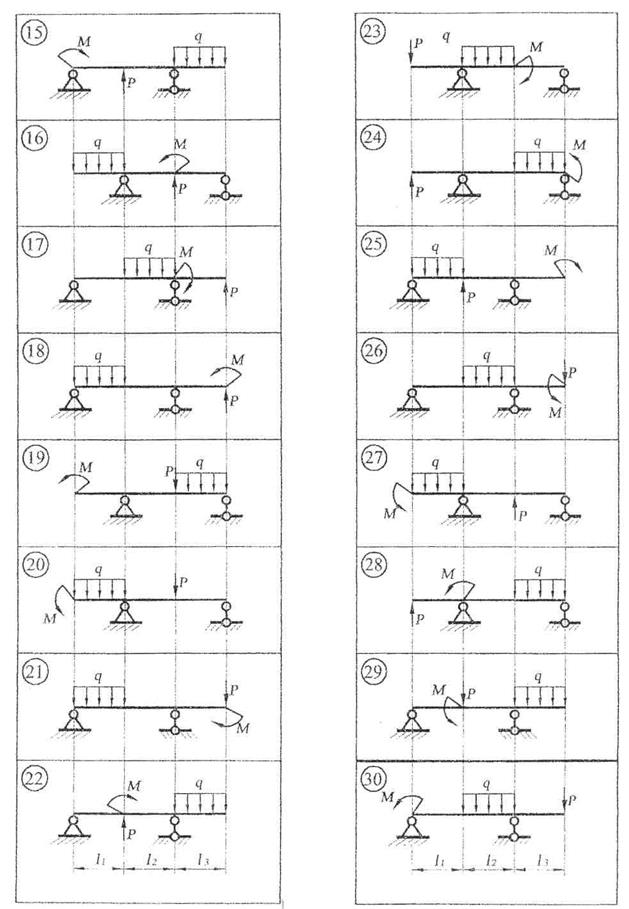
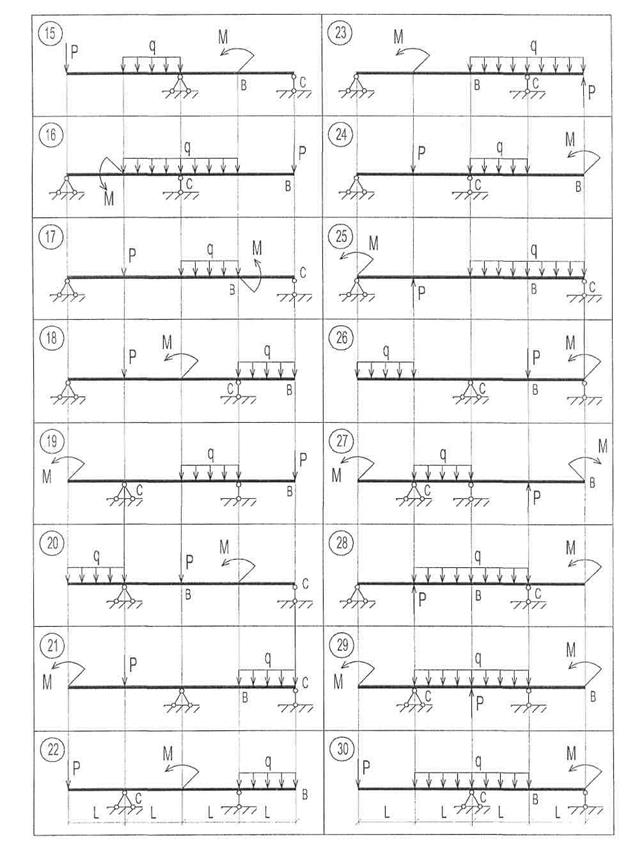
Рис. 7. Схемы к задаче 3.2
|
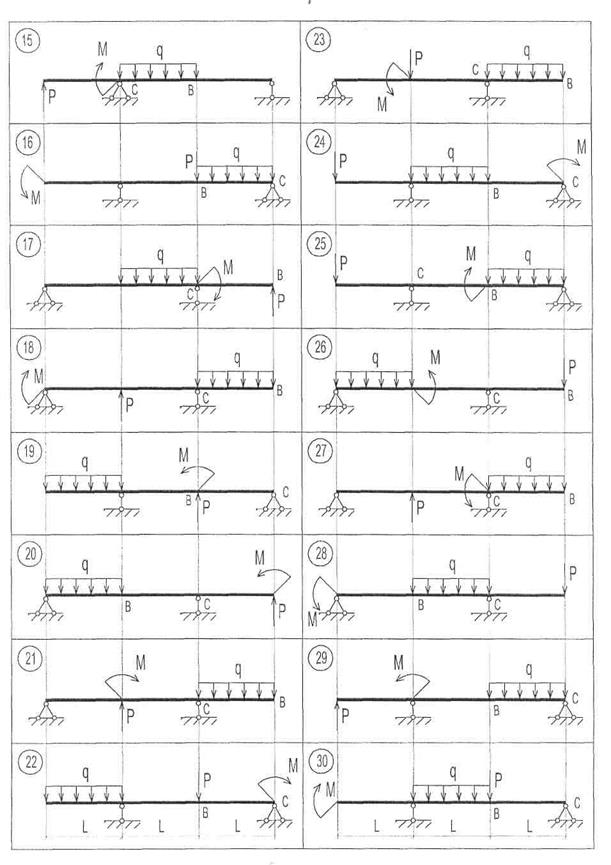
Рис. 7. Продолжение
|
Рис. 8. Схемы к задаче 3.3

|
Рис. 8. Продолжение
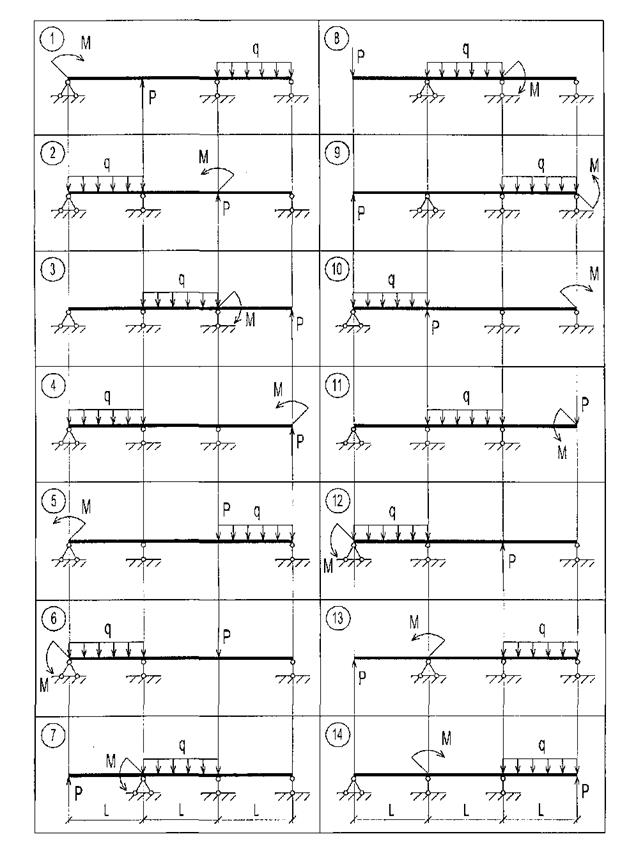
|
Рис. 9. Схемы к задаче 4.1

|
Рис. 9. Продолжение
|
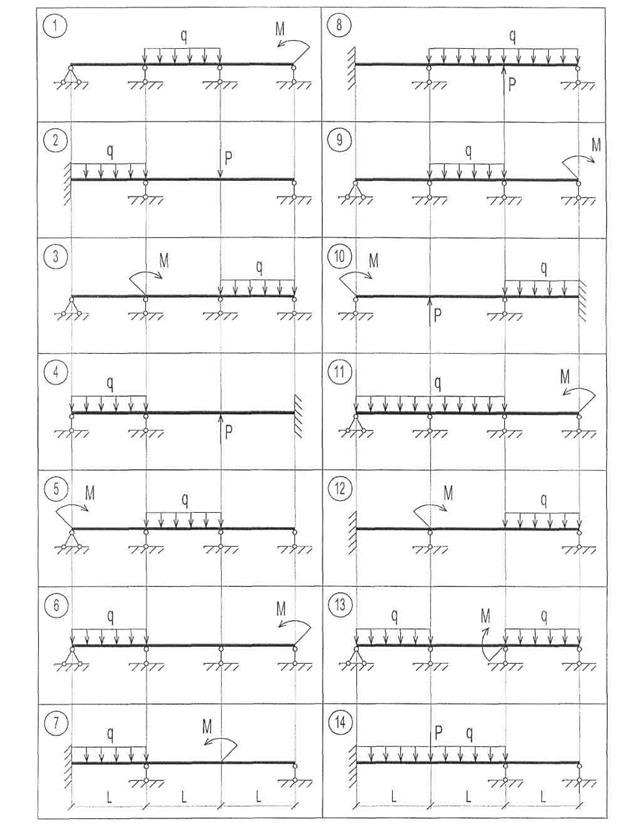
Рис. 10. Схемы к задаче 4.2
|
Рис. 10. Продолжение

|
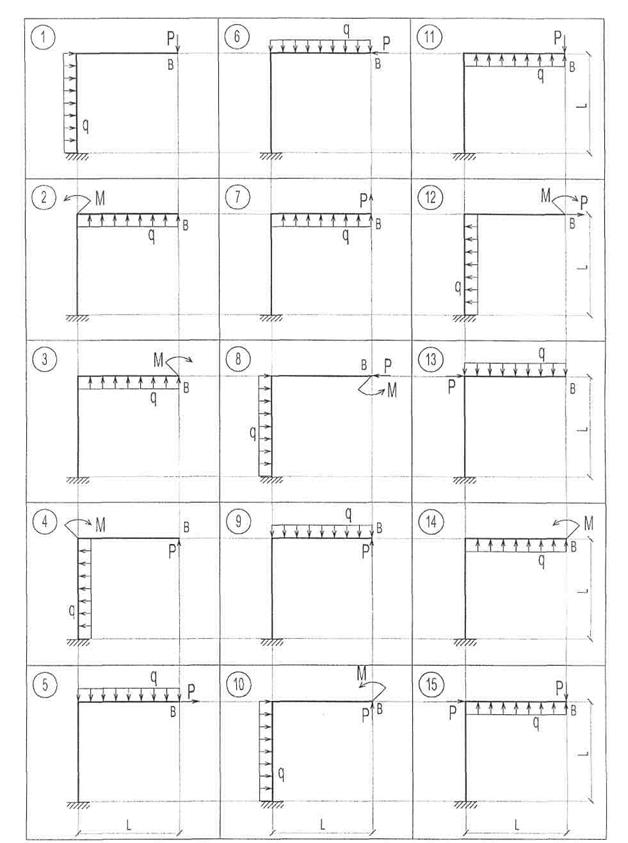
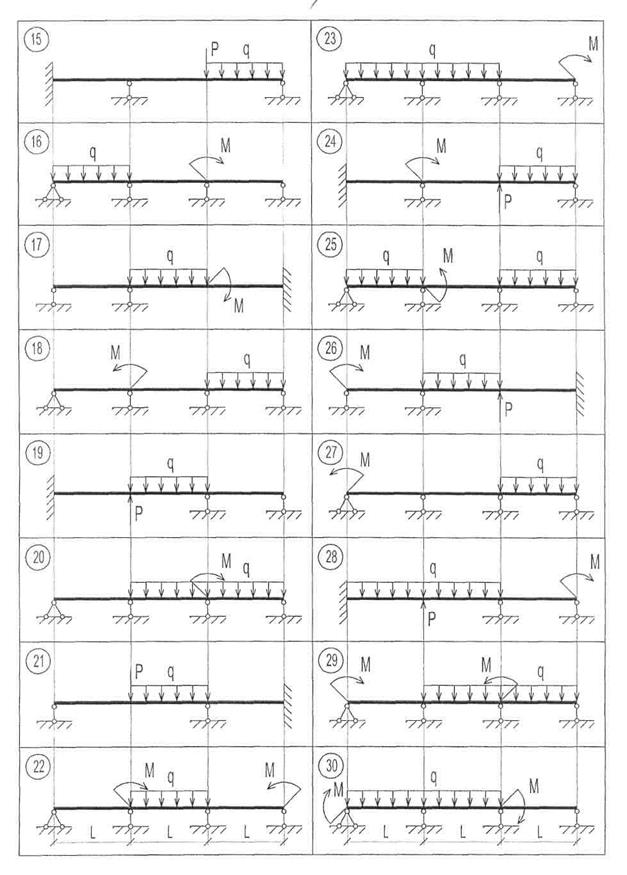
Рис. 11. Схемы к задаче 5.1
|
Рис. 11. Продолжение
|
Рис. 11. Продолжение
|
Рис. 12. Схемы к задаче 5.2
|
Рис. 13. Схемы к задаче 6.1

|
Рис. 13. Продолжение
|
Рис. 13. Продолжение





Библиографический список
Беляев Н.М. Сборник задач по сопротивлению материалов. М.: Наука, 1972. 348 с.
Зубчанинов В.Г. Сопротивление материалов: Учебное пособие.2-е изд. Тверь: ТГТУ, 2003. Кн.1. 224 с.
Зубчанинов В.Г. Лекции по механике деформируемого твердого тела: В 3 ч. Тверь: ТвеПИ, 1993. 441 с.
Зубчанинов В.Г, Гараников В.В., Ведерников В.Н. Лабораторный практикум по сопротивлению материалов. Тверь: ТГТУ, 2007. 132 с.
Лабораторный практикум по сопротивлению материалов деформированию. /Под ред. П.М. Огибалова и И.А. Скорого. М.: МГУ, 1961. 197 с.
Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. Киев: Наук. Думка, 1975. 704 с.
Феодосьев В.И. Сопротивление материалов. М.: Наука, 1974. 559с.;
1986. 512с.
Оглавление
Содержание курсовой работы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..3
Оформление курсовой работы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . …3
Защита курсовой работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..3
Задание I. Построение эпюр внутренних силовых факторов
при растяжении-сжатии, кручении и прямом плоском изгибе
с расчетами на прочность и жесткость…………………………………………..5
Дата добавления: 2014-12-06; просмотров: 1930;
