ИДЗ-4. Классическое определение вероятности. Решите задачу на вычисление вероятности, основываясь на ее классическом определении.

Решите задачу на вычисление вероятности, основываясь на ее классическом определении.

Из множества всех последовательностей длины 10, состоящих из цифр 0; 1; 2; 3, наудачу выбирается одна. Какова вероятность того, что выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности.

Решение: Вероятность события A – «Выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности», согласно классическому определению, равна

P(A) = ,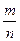

где n – полное число равновероятных исходов; m – число исходов, благоприятствующих событию A.

Число способов заполнить 10 позиций в последовательности цифрами 0; 1; 2; 3 составляет, с учетом возможности повторения цифр,

n = 4¹⁰ = 2²⁰ = 1048576.

Число способов разместить 5 нулей на 10 позициях в последовательности при условии, что нули обязательно находятся на первом и десятом месте в последовательности, равно числу способов разместить три нуля на восьми свободных позициях в последовательности и равно числу сочетаний из 8 элементов по 3: 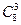= = 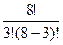56. Оставшиеся 8 – 3 = 5 позиций в последовательности будут заполнены цифрами 1; 2; 3. Число способов осуществить это, с учетом возможности повторения, равно 3⁵ = 243. Т.о., число исходов, благоприятствующих событию A, равно

m = 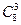´3⁵ = 56×243 = 13608.

Искомая вероятность события A равна:

P(A) = 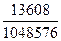= 0,013.

Ответ: P(A) = 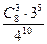= 0,013.

Варианты индивидуальных домашних заданий (ИДЗ)

ИДЗ-1. Основные понятия теории множеств

Определить и изобразить на рисунках множества A, B, AÈB, AÇB, A/B, B/A, ADB:

1.A = {(x, y) Î R²: x £ y}, B = {(x, y) Î R²: |x| + |y| £ 1};

2.A = {(x, y) Î R²: y £ –x}, B = {(x, y) Î R²: x² + y² £ 1};

3.A = {(x, y) Î R²: y £ x²}, B = {(x, y) Î R² : x² + (y – 1)² £ 1};

4.A = {(x, y) Î R²: x×y ³ 0}, B = {(x ,y) Î R²: x² + y² ³ 1};

5.A = {(x, y) Î R²: y £ –x²}, B ={(x, y) Î R²: (x + 1)² + (y + 1)² £ 1};

6.A = {(x, y) Î R²: x×y £ 0}, B ={(x, y) Î R²: |x| + |y| ³ 1};

7.A = {(x, y) Î R²: x ³ y}, B = {(x, y) Î R²: 9x² + y² £ 36};

8.A = {(x, y) Î R²: x £ y}, B ={(x, y) Î R²: 4x² + 9y² ³ 36};

9.A = {(x, y) Î R²: max{|x|, |y|} £ 1}, B = {(x, y) Î R²: x² + y² £ 1};

10.A = {(x, y) Î R²: max{|x|, |y|} £ 2}, B= {(x, y) Î R²: y ³ x + 1};

11.A = {(x, y) Î R²: y ³ x²}, B = {(x, y) Î R²: y £ 4 – x²};

12.A = {(x, y) Î R²: x £ –y}, B = {(x, y) Î R² : |x| + |y| £ 2};

13.A ={(x, y) Î R²: |x| + |y| ³ 3}, B = {(x, y) Î R²: max{|x|, |y|} £ 2};

14.A = {(x, y) Î R²: y £ –x²}, B = {(x, y) Î R²: (x – 1)² + (y + 1)² £ 1};

15.A = {(x, y) Î R²: x×y £ 0}, B = {(x, y) Î R²: x² + (y + 1)² ³ 1};

16.A = {(x, y) Î R²: x×y £ 0}, B = {(x, y) Î R²: x² + y² ³ 4};

17.A = {(x, y) Î R²: y £ x²}, B = {(x, y) Î R²: (x – 1)² + (y + 1)² £ 4};

18.A = {(x, y) Î R²: x² £ y}, B = {(x, y) Î R²: x² + y² ³ 4};

19.A = {(x, y) Î R²: x×y ³ 0}, B = {(x, y) Î R²: |x| + |y – 2| ³ 1};

20.A = {(x, y) Î R²: x £ –y}, B = {(x, y) Î R²: (x – 2)² + (y + 3)² ³ 1};

21.A = {(x, y) Î R²: x £ y}, B = {(x, y) Î R² : 9x² + y² £ 9};

22.A = {(x, y) Î R²: x ³ y}, B = {(x, y) Î R²: x² + 4y² ³ 4};

23.A = {(x, y) Î R²: |x| + |y| £ 2}, B = {(x, y) Î R²: 9x² + y² ³ 9};

24.A = {(x, y) Î R²: max{|x|, |y|} £ 2}, B = {(x, y) Î R²: x² + 1 £ y};

25.A = {(x, y) Î R²: max{|x|, |y|} £ 2}, B = {(x, y) Î R²: 4 – x² ³ y};

26.A = {(x, y) Î R²: x×y £ 1}, B = {(x, y) Î R² : x² + y² £ 9};

27.A = {(x, y) Î R²: x² + y² £ 4}, B = {(x, y) Î R²: (x + 1)² + (y + 1)² £ 4};

28.A = {(x, y) Î R²: |x| + |y| ³ 4}, B = {(x, y) Î R²: x² + y² £ 16};

29.A = {(x, y) Î R²: y ³ (x – 2)²}, B = {(x, y) Î R²: x² + y² £ 4};

30.A = {(x, y) Î R²: x + y £ 3}, B = {(x, y) Î R²: (x – 1)² + (y – 1)² £ 9}.