ИДЗ-2. Законы алгебры множеств

Пусть A, B, C – подмножества некоторого универсального множества U. Установите справедливость нижеследующего утверждения:

(A\B)È(B\A) = (AÈB)\(AÇB).

Решение: Разложим множества A и B на непересекающиеся подмножества {x_A}, {x_B}, {x_AB}:

A = {x_AÈx_AB};

B = {x_BÈx_AB}.

В этих обозначениях для левой части предполагаемого равенства имеем:

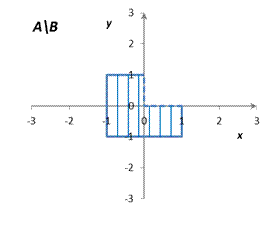
A\B = {x_AÈx_AB}\{x_BÈx_AB} = {x_A};

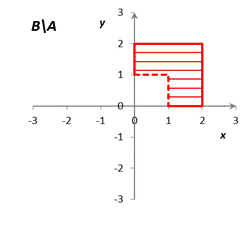
B\A = {x_BÈx_AB}\{x_AÈx_AB} = {x_B};

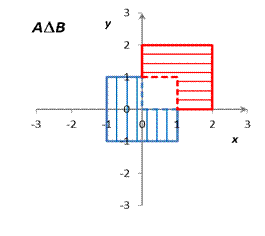
(A\B)È(B\A) = {x_A}È{x_B} = {x_AÈx_B}.

Для правой части равенства имеем:

AÈB = {x_AÈx_AB}È{x_BÈx_AB} = {x_AÈx_BÈx_AB};

AÇB = {x_AÈx_AB}Ç{x_BÈx_AB} = {x_AB};

(AÈB)\(AÇB) = {x_AÈx_BÈx_AB}\{x_AB} = {x_AÈx_B}.

Левая и правая части доказываемого равенства одинаковы и равны {x_AÈx_B}. Справедливость утверждения установлена.

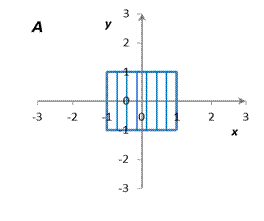
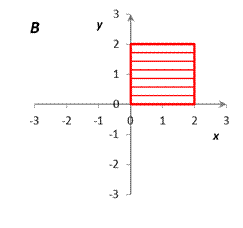
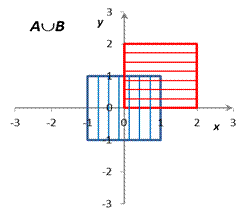
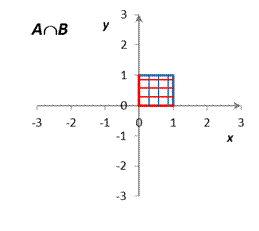
	Рис. 1