Подходы к оценке криптографической стойкости шифров

В криптографии разработаны два базовых подхода в оценке стойкости шифров. Основы первого подхода (совершенная секретность) К. Шеннон изложил в своей работе в 1948 г.

Другой подход к определению стойкости берет начало в той же работе Шеннона и называется практической стойкостью или сложностный подход к стойкости.

Первый подход к оценке стойкости шифров

В криптографии разработаны два базовых подхода в оценке стойкости шифров. Основы первого подхода (совершенная секретность) К. Шеннон изложил в своей работе в 1948 г. Рассмотрим этот подход. К. Шеннон предложил следующую модель обращения с параметрами, описывающую шифрование и действия противника. Пусть

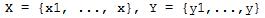- множества открытых сообщений и возможных шифртекстов. Открытый текст для передачи в шифрованном виде выбирается случайно в соответствии с распределением

.

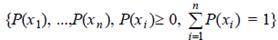Тогда при решении задачи вскрытия x по известному у противник может вычислить апостериорные вероятности сообщений, которые могли быть посланы 5.png, s=1,...,n. Если задача дешифрования решена и открытый текст найден, то апостериорное распределение вырождено:

6.png при s ≠ i .

Таким образом в апостериорных вероятностях {Р(х|у), x ∈X} отображаются даже частичные сведения об открытом тексте, полученном при перехвате криптограммы. Шеннон определил совершенную секретность (стойкость) шифра условием: апостериорные распределения на открытых текстах при любом у∈Y совпадают с априорным распределением на Х, т.е. Р(х|у) = Р(х) для любых x ∈X, у ∈Y.

Апостериорное распределение - условное распределение вероятностей какой-либо случайной величины при некотором условии, рассматриваемое в противоположность ее безусловному или априорному распределению.

Если 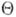- случайный параметр с априорной плотностью 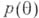, , 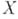- случайный результат наблюдений и 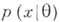- условная плотность Xпри условии 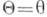, то А. р. 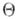при данном Xсогласно Вейеса формуле имеет плотность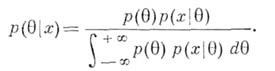

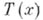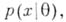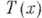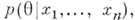Если - достаточная статистика для семейства распределений с плотностями то А. р. зависит не от самого г, а от. Асимптотич. поведение при А. р. где 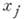суть результаты независимых наблюдений с плотностью 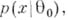оказывается "почти независящим" от априорного распределения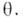

Сопряжённое априорное распределение — одни из основных понятий в байесовской статистике.

Рассмотрим задачу о нахождении распределения параметра 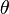(рассматриваемого как случайная величина) по имеющемуся наблюдению x. По теореме Байеса, апостериорное распределение вычисляется из априорного распределения с плотностью вероятности 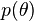и функции правдоподобия 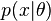) по формуле:

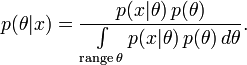Если апостериорное распределение 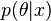принадлежит тому же семейству вероятностных распределений, что и априорное распределение 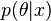(т.е. имеет тот же вид, но с другими параметрами), то это семейство распределений называется сопряжённым семейству функций правдоподобия 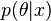. При этом распределение 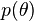называется сопряжённым априорным распределением к семейству функций правдоподобия .

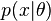Знание сопряжённых семейств распределений существенно упрощает вычисление апостериорных вероятностей в байесовской статистике, так как позволяет заменить вычисление громоздких интегралов в формуле Байеса простыми алгебраическими манипуляциями над параметрами распределений.

Шифротекст — результат операции шифрования. Часто также используется вместо термина «криптограмма», хотя последний подчёркивает сам факт передачи сообщения, а не шифрования.

Процесс применения операции шифрования к шифротексту называется перешифровкой.