Интегрирование правильной дробно-рациональной функции
Сразу пример и типовой алгоритм решения интеграла от дробно-рациональной функции.
Пример 1
Найти неопределенный интеграл.
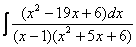
Шаг 1.Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как:
Сначала смотрим на числитель и выясняем старшую степень многочлена:
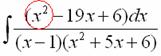
Старшая степень числителя равна двум.
Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень
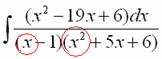
и мысленно умножаем: 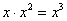 – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.
– таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.
Вывод: Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной.
Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной.
Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.
Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель:
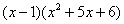
Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение:
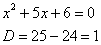
Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители:
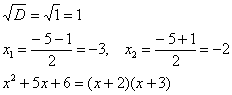
Дата добавления: 2014-11-29; просмотров: 1645;
