КІНЕМАТИЧНІ РОЗРАХУНКИ
3.1 Загальні розрахунки
Передаточне відношення кожного простого механізма (передачі) визначають за формулами:
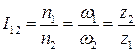 , інакше: , інакше: 
| (3.1.) |
Спільне передаточне відношення визначають за формулою:
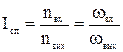
| (3.2.) |
або для складного механізма
| Ісп =І1 × І2 × І3 × ... × Іm | (3.3.) |
де
І1 ; І2 ; ... Im, передаточні відношення окремих передач;
Частоти обертання всіх валів з закріпленими на них колесами визначають
( при розрахунку в напрямі від входа до вихідного вала):
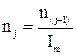
| (3.4.) |
де nj – частота обертання j-того вала;
n(j-1) – частота обертання (j-1)-того (попереднього) вала;
Іm– передаточне відношення зубчастої передачі між цими валами;
Оскільки всі формули з кінематичних розрахунків простих і складних зубчастих механізмів, детально надані в лекційному матеріалі та
підручниках, в Методичних вказівках додатково надається інформація про планетарні передачі, сприйняття яких Студентами дещо ускладнене.
3.2 Кінематика планетарних передач
При кінематичних розрахунках планетарних передач визначаються частоти обертання всіх ланок механізму та кількість зубців коліс, при цьому використовується метод зупинки водила (метод Вілліса). Сутність методу полягає в тому, що всім ланкам передачі умовно надається частота обертання водила, але протилежна за напрямком обертання ("-nн"). В результаті отримаємо так званий обернений механізм, у якого водило і геометричні осі зубчастих коліс нерухомі.
Для оберненого механізму складають кінематичні рівняння, за допомогою яких визначаються кінематичні параметри реального механізму. При цих розрахунках враховуються знаки кінематичних параметрів. Передаточне відношення зовнішнього зачеплення береться зі знаком "-", а внутрішнього – зі знаком "+".
Для подальшого розгляду приймаються такі позначення для параметрів реального і оберненого механізмів:
- nc, ng, nн, ns – частоти обертання ланок реального механізму: сонячного колеса, сателіта першої групи, водила та сателіта другої групи відповідно;
- Існ= 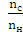 – передаточне відношення реального механізму;
– передаточне відношення реального механізму;
- 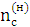 ,
, 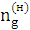 ,
, 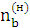 – частоти обертання ланок оберненого механізму: сонячного колеса, сателіта групи, та колеса b відповідно;
– частоти обертання ланок оберненого механізму: сонячного колеса, сателіта групи, та колеса b відповідно;
- 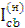 ,
, 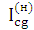 , – передаточні відношення в оберненому механізмі;
, – передаточні відношення в оберненому механізмі;
Приклад наведено в кінці розділу.
3.2.1 Кінематика одноступінчастої планетарної передачі
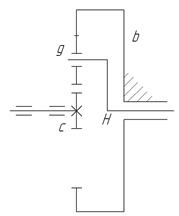 |
Рис.1
Кінематична схема одноступінчастої планетарної передачі
Кінематичні рівняння
| а) |  = = 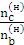 = = 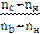
| (3.5.) |
де 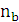 = 0;
= 0;
b)  = -
= - 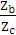 .
.
| а) | 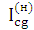 = =  = = 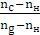
| (3.6.) |
b) 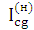 = -
= - 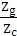 .
.
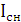 = = 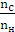 = 1- = 1- 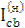
| (3.7.) |
В рівнянні (3.7) 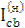 < 0 (див. 3.5.1b), тобто
< 0 (див. 3.5.1b), тобто 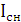 > 0.
> 0.
Додатнє значення 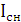 означає, що колесо С і водило Н в реальному механізмі мають однакові напрямки обертання, якщо дивитись з одного боку.
означає, що колесо С і водило Н в реальному механізмі мають однакові напрямки обертання, якщо дивитись з одного боку.
Приклад. Визначити частоти обертання nc, ng, 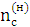 ,
, 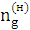 ,
, 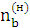 передачі, зображеної на рис.1, якщо Zc=24, Zb=84, Zg=30, nн=100[
передачі, зображеної на рис.1, якщо Zc=24, Zb=84, Zg=30, nн=100[ 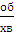 ].
].
Розв¢язок:
1) Визначається nc: з рівності 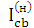 =
= 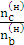 =
= 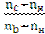 ;
; 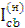 = -
= - 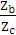 = -3.5 .
= -3.5 .
Таким чином, nc = - 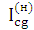 nн + nн = - (-3.5)·100 + 100 = 450 [
nн + nн = - (-3.5)·100 + 100 = 450 [ 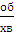 ].
].
Можна і так: 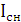 =
= 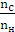 = 1 –
= 1 – 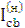 = 1 – (-3.5) = 4,5 .
= 1 – (-3.5) = 4,5 .
Звідси nc = 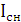 nн = 4,5 · 100 = 450 [
nн = 4,5 · 100 = 450 [ 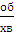 ].
].
2) Визначається ng:
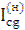 =
=  =
= 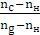 ; або
; або 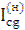 = -
= - 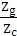 = -
= - 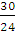 = -1.25 .
= -1.25 .
Звідси ng = 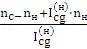 =
= 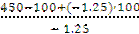 = -180 [
= -180 [ 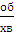 ].
].
Можна і так: 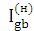 =
= 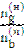 =
= 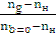 ;
; 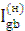 =
= 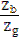 =
= 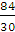 = 2,8 .
= 2,8 .
Звідси ng= - 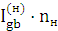 +
+ 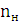 = -2,8 ·100+100 = -180[
= -2,8 ·100+100 = -180[ 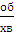 ].
].
3) Визначається 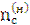 ,
, 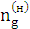 ,
, 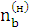 :
:
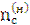 =
= 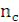 –
– 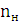 = 450 – 100 = 350[
= 450 – 100 = 350[ 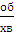 ].
].
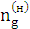 =
= 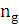 –
– 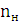 = - 180 – 100 = -280[
= - 180 – 100 = -280[ 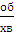 ].
].
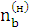 =
= 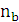 –
– 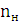 = -
= - 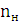 = - 100[
= - 100[ 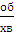 ].
].
 3.2.2. Кінематика двоступінчастої планетарної передачі зі змішаним зачепленням
3.2.2. Кінематика двоступінчастої планетарної передачі зі змішаним зачепленням
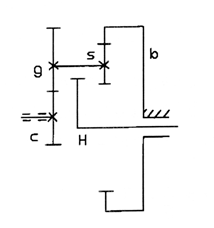
Рис.2
Кінематична схема двохступінчастої планетарної передачі
Кінематичні рівняння для цієї передачі:
| а) | 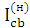 = = 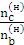 = = 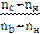
| (3.8.) |
b) 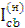 =
= 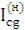 ·
· 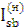 = -
= - 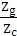 ·
· 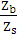 ,
,
| а) | 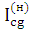 = =  = = 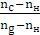
| (3.9.) |
b) 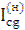 = -
= - 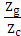 ,
,
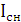 = = 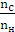 = 1 - = 1 - 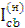
| (3.10.) |
В рівнянні (3.10) 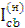 < 0 (див. 3.8 b), тобто
< 0 (див. 3.8 b), тобто 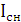 > 0 .
> 0 .
Це означає, що колесо С і водило Н обертаються в одну сторону, якщо дивитися з одної сторони на механізм.
Розглянемо приклад.
Приклад. Визначити частоти обертання 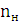 , ng,
, ng, 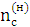 ,
, 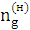 ,
, 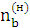 передачі, зображеної на рис.2, якщо Zc=36, Zb=135, Zg=72, Zs=27, nс=1100[
передачі, зображеної на рис.2, якщо Zc=36, Zb=135, Zg=72, Zs=27, nс=1100[ 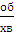 ].
].
Розв¢язок:
1) Визначається 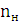 :
:
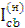 =
= 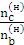 =
= 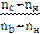 ;
; 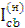 =
= 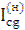 ·
· 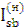 = -
= - 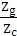 ·
· 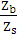 = -
= - 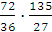 = -10 .
= -10 .
Звідси 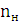 =
=  =
= 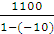 = 100 [
= 100 [ 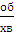 ];
];
Або так: 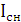 =
= 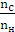 = 1 -
= 1 - 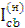 = 1- (-10) = 11;
= 1- (-10) = 11;
Звідси 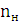 =
= 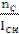 =
= 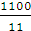 = 100 [
= 100 [ 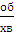 ];
];
2) Визначається ng:
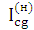 =
=  =
= 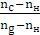 , або
, або 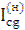 = -
= - 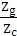 = -
= - 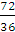 = -2
= -2
Звідси ng = 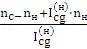 =
= 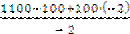 = - 400[
= - 400[ 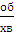 ];
];
Або так: 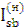 =
= 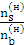 =
=  ,
,
звідси 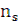 =
= 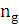 = -
= - 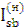 ·
· 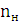 +
+ 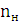 = -5 · 100 + 100 = - 400 [
= -5 · 100 + 100 = - 400 [ 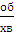 ].
].
3) Визначається 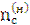 ,
, 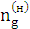 ,
, 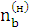 :
:
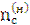 =
= 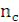 –
– 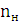 = 1100 – 100 = 1000 [
= 1100 – 100 = 1000 [ 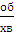 ].
].
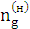 =
= 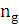 –
– 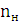 = - 400 – 100 = - 500 [
= - 400 – 100 = - 500 [ 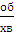 ].
].
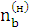 =
= 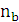 –
– 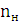 = -
= - 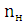 = -100 [
= -100 [ 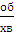 ].
].
3.2.3. Визначення кількості зубців коліс планетарних передач
На підбір кількості зубців коліс планетарних передач, окрім відомої вимоги  ³ 17, накладається ряд додаткових умов.
³ 17, накладається ряд додаткових умов.
До них відносяться:
1) умова соосності входу і виходу передачі;
2) умова складання, яка повинна виконуватись при кратності зубців центральних коліс кількості сателітів;
3) умова сусідства сателітів, що забезпечує гарантований зазор між сателітами;
Ці умови враховані при виведенні формул визначення кількості зубців коліс для схем планетарних передач, які застосовуються найчастіше.
Одноступінчаста планетарна передача (Рис.1)
Використовуються формули підбору кількості зубців, що вказані нижче:
Zc = a × k × 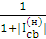
| (3.11.) |
де: a –довільне ціле додатнє число;
k – кількість сателітів.
Zb = 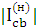 · Zc · Zc
| (3.12.) |
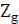 = = 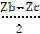 ; ;
| (3.13.) |
обов¢язкова перевірка умова сусідства сателітів:
(Zc+ 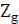 ) · Sin ) · Sin 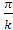 > > 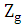 +2 +2
| (3.14.) |
Приклад. Визначити число зубців коліс c, b, g одноступінчастої планетарної передачі, якщо відомо, що 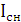 =4.2, k=3.
=4.2, k=3.
Розв¢язок:
1) Визначається Zc:
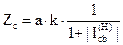 ; тут
; тут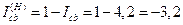
підставляється в формулу для 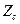 :
:
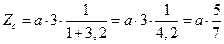 ;
;
Примітка: При розрахунках десятичні дробі пареводять в звичайні, оскільки це спрощує процес розрахунку.
Підбирається параметр а таким чином, щоб 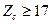 і Zc було кратним кількості сателітів k.
і Zc було кратним кількості сателітів k.
Наприклад приймаємо а=42, тоді 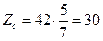
2) Визначається  :
:
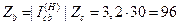
3) Визначається 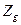 :
:
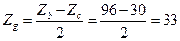
4) Перевіряється умова сусідства сателітів:
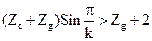 ;
;
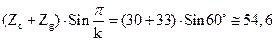
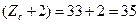
Розрахунки свідчать, що умова сусідства сателітів виконується.
Примітки:
1. Кількість зубців коліс не повинні бути дробовими числами;
2. Заокругленнякількості зубців коліс до цілого числа не допускається.
3. Кількість зубців центральних коліс 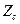 і
і  мають бути кратні кількості сателітів k.
мають бути кратні кількості сателітів k.
4. Кількість зубців кожного з коліс повинна відповідати умові: Zі > 17
Двоступінчаста планетарна передача зі змішаним зачепленням (Рис.2)
Формули підбору кількості зубців:
| 1) | 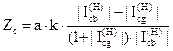
| (3.15.) |
тут 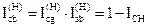
Рекомендується приймати 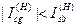
| 2) | 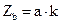 ; ;
| (3.16.) |
| 3) | 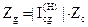
| (3.17.) |
| 4) | 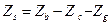
| (3.18.) |
5) Умова сусідства сателітів:
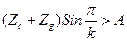 ; ; 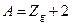 , якщо , якщо 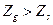
| (3.19.) |
і 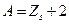 , якщо
, якщо 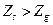 .
.
Примітки.
1. Кількість зубців кожного з коліс повинна відповідати умові: Zі > 17;
2. Кількість зубців центральних коліс 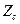 і
і  мають бути кратні кількості сателітів к;
мають бути кратні кількості сателітів к;
3. Кількість зубців коліс не повинна бути дробовим числом;
4. Заокругленнякількості зубців колісдо цілого числа не допускається.
5. Формули підбору кількості зубців отримані для випадку, коли модулі зубчатих коліс зовнішнього і внутрішнього зачеплення однакові.
Приклад. Визначити кількість зубців коліс c, g, b, s, передачі зі змішаним зачепленням (Рис.2), якщо 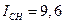 , k=3.
, k=3.
Розв¢язок: 1) Визначається 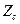 :
:
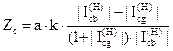 ; тут
; тут 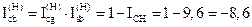 ;
;
Приймаємо 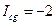 , тоді
, тоді 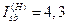 ; десятковий дріб 8,6 перетворюється у неправильний простий дріб
; десятковий дріб 8,6 перетворюється у неправильний простий дріб 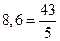 , підставляється в вираз для
, підставляється в вираз для 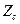 :
:
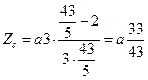 ; Наприклад приймаємо а = 43, тоді
; Наприклад приймаємо а = 43, тоді 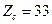 .
.
2) Визначається  :
: 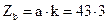 .
.
3) Визначається 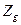 :
: 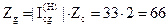 .
.
4) Визначається 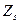 :
: 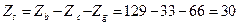 .
.
6. Перевіряється умова сусідства сателітів
В прикладі 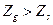 , тобто умова сусідства сателітів:
, тобто умова сусідства сателітів:
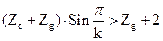
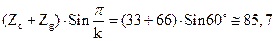
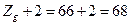 Умова сусідства виконується.
Умова сусідства виконується.
Двоступінчаста планетарна передача з двома зовнішніми зачепленнями
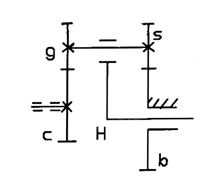 |
(Рис.3)
Формули підбору кількості зубців:
| 1) | 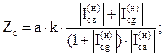
| (3.20.) |
тут 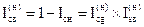
рекомендується приймати 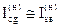 ;
;
| 2) | 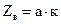
| (3.21.) |
| 3) | 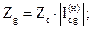
| (3.22.) |
| 4) | 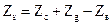
| (3.23.) |
Умова сусідства сателітів:
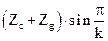 > А; А > А; А 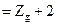 , якщо , якщо 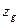 > > 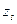
| (3.24.) |
А 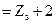 , якщо
, якщо 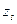 >
> 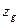
Дата добавления: 2014-12-04; просмотров: 1916;
