Лекция №3 Классификация погрешностей. Правила округления результатов измерений
Погрешностью называется отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Истинное значение величины неизвестно, его применяют только в теоретических исследованиях. На практике используют действительное значение величины Хд в результате чего погрешность измерения ΔХизм определяют по формуле:
ΔХизм = Хизм - Хд
где Хизм - измеренное значение величины.
Классификация погрешностей[8]
| Систематическая погрешность | Составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. |
| Инструментальная погрешность | Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений |
| Погрешность метода измерений | Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений. |
| Погрешность (измерения) из-за изменений условий измерения | Составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения. |
| Субъективная погрешность измерения | Составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора. |
| Неисключенная систематическая погрешность | Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости. |
| Случайная погрешность измерения | Составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. |
| Абсолютная погрешность измерения | Погрешность измерения, выраженная в единицах измеряемой величины. |
| Относительная погрешность измерения | Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины. |
Относительную погрешность в долях или процентах находят из отношений:
δ = ΔХ/Х или δ = (ΔХ/Х)*100%
где:
ΔХ - абсолютная погрешность измерений;
Х - действительное или измеренное значение величины.
Cреднее квадратическое отклонение[9] результатов единичных измерений в ряду измерений представляет собой оценку S[10] рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле:
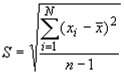
где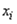 
- результат 
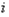-го единичного измерения;
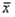- среднее арифметическое значение измеряемой величины из 
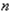единичных результатов.
Оценка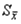 
случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле
,
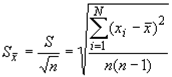где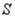 
- среднее квадратическое отклонение и результатов единичных измерений, полученная из ряда равноточных измерений; 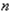- число единичных измерений в ряду.
К числовым характеристикам случайных погрешностей, как любых случайных величин относятся:
1. математическое ожидание т.е. Сумма произведений всех возможных значений случайных погрешностей на вероятность этих значений: M = ∑XiPi
2. дисперсия (математическое ожидание квадрата соответствующей центрированной погрешности) D = ∑(Xi-M)2Pi
3. среднее квадратическое отклонение, как положительный корень квадратный из дисперсии: σ = √D
Лекция №4 Грубые погрешности измерений (промахи)
Промах - погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Основной вид промахов — ошибки наблюдателя во время измерения. Однократные измерения не позволяют обнаружить грубую погрешность, поэтому наиболее ответственные измерения производят несколько раз. Среднее арифметическое полученных значений принимают за результат. Отбрасывание промахов в этом случае производят согласно статистических критериев, при этом необходимо знать какому виду (закону) распределения плотности вероятности случайной величины принадлежит результат.
Рассмотрим некоторые из этих критериев.
Дата добавления: 2014-12-04; просмотров: 891;