ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
К полупроводникам относят класс веществ, характеризующихся значениями удельной электропроводности g, промежуточными между удельной электропроводностью металлов и хороших диэлектриков. В отличие от металлов, электропроводность полупроводников увеличивается с ростом температуры:
g = g0 ехр [-ЕА/(kT)], (9.1)
где ЕА – энергия активации проводимости, g0 – коэффициент (изменяется с температурой значительно медленнее, чем экспоненциальный множитель). Формула (9.1) означает, что в полупроводниках энергия связи электронов с атомами имеет порядок ЕА. При повышении температуры тепловое движение разрывает связи электронов, и часть последних в количестве, пропорциональном экспоненте ехр[-ЕА/kT)], становится свободными носителями заряда.
Связь электронов с атомами может быть разрушена также внешними воздействиями: светом, потоком быстрых частиц, сильным электрическим полем и т.д. Поэтому электропроводность полупроводниковых кристаллов чувствительна к внешним воздействиям, а также к содержанию дефектов и примесей в решетке. Во многих случаях энергия ЕА электронов, локализованных вблизи примесей и дефектов, существенно меньше, чем в идеальном полупроводниковом кристалле. Возможность управлять в широких пределах электропроводностью полупроводников изменением температуры, напряженности внешних полей и введением примесей является основой их многочисленных и разнообразных применений.
9.1 Зонная структура
Движение носителей заряда в полупроводниках описывает зонная теория твердого тела. В полупроводниках верхняя из заполненных разрешенных зон (валентная) отделена от самой низкой из незаполненных зон (зоны проводимости) энергетической щелью Eg (запрещенная зона). Тепловое движение «забрасывает» часть электронов из валентной зоны в зону проводимости, что обусловливает появление в валентной зоне дырок (рис. 9.1).


Электроны и дырки обычно сосредоточены вблизи дна зоны проводимости или потолка валентной зоны на энергетических расстояниях от них ~ kT, что гораздо меньше ширины разрешенных зон.
Ширина запрещенной зоны полупроводников меняется в широких пределах (табл. 9.1). Так, при Т ® 0 К Еg = 0,165 эВ в PbSe и 5,6 эВ в алмазе, а серое олово – пример так называемого бесщелевого полупроводника, у которого Еg = 0.
Таблица 9.1 Ширина запрещенной зоны некоторых полупроводников при Т = 300 К
| Полупроводник | Eg, эВ | Полупроводник | Eg, эВ |
| Химические элементы | Соединения AIIBVI | ||
| Si | 1,107 | ZnS | 3,6 |
| Ge | 0,66 | CdS | 2,42 |
| Te | 0,33 | CdSe | 1,8 |
| Se | 1,79 | ZnSe | 2,7 |
| Соединения AIIIBV | Соединения AIVBVI | ||
| GaAs | 1,428 | PbS | 0,41 |
| InAs | 0,356 | SnS | 1,08 |
| GaSb | 0,78 | PbTe | 0,32 |
| GaP | 2,24 | SnTe | 0,18 |
9.2 Собственная и примесная проводимость
Электропроводность полупроводников может быть обусловлена собственными электронами атомов данного вещества (собственная проводимость) и электронами примесных атомов (примесная проводимость). Источниками носителей тока могут быть также дефекты кристаллической структуры (вакансии, междоузельные атомы и др.)
Собственная проводимость. Электропроводность полупроводника, не содержащего примесей и дефектов, при Т = 0 К равна нулю, поскольку в нем нет свободных носителей заряда. Действительно, его валентная зона полностью заполнена электронами и не дает никакого вклада в проводимость, а зона проводимости пуста. При Т > 0 К появляется вероятность заброса электронов из валентной зоны в зону проводимости (см. рис. 9.1). В результате в валентной зоне образуются дырки, причем концентрации электронов n и дырок р будут одинаковы. Одновременно с процессом образования свободных носителей (генерация) идет процесс их исчезновения (рекомбинация), т.е. возврат части электронов из зоны проводимости в валентную зону и заполнение дырок. При температуре, отличной от абсолютного нуля, в полупроводниках устанавливается некоторая равновесная концентрация носителей заряда. Так, например, при комнатной температуре концентрация свободных электронов и дырок составляет в Si примерно 1010 см–3, а в Ge ~1013 см–3.
При наложении электрического поля Е в полупроводнике возникает ток, состоящий из электронной и дырочной составляющих. Полупроводники, в которых за счет перехода некоторого количества электронов из валентной зоны в зону проводимости образуется такое же количество дырок, называются собственными. Соответственно их проводимость, состоящую из электронной и дырочной составляющих, называют собственной проводимостью.
Результирующая электропроводность собственного полупроводника определяется суммой электронной и дырочной компонент:
g = enun + epup, (9.2)
где un и up – подвижности электронов и дырок соответственно. В уравнение (9.2) входят два важнейших параметра полупроводника – концентрация (n, p) и подвижность носителей зарядов.
Концентрация носителей (электронов и дырок) в собственном полупроводнике увеличивается с ростом температуры по экспоненциальному закону:
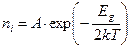 , (9.3)
, (9.3)
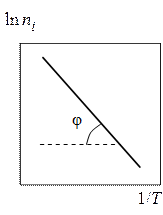
где А – коэффициент, слабо зависящий от температуры. Энергия активации этого процесса равна половине ширины запрещенной зоны Еg/2. Температурная зависимость концентрации собственных носителей, построенная в координатах 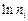 от 1/Т имеет вид:
от 1/Т имеет вид:
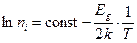 , (9.4)
, (9.4)
и представляет собой практически прямую линию (рис. 9.2). Тангенс угла наклона этой прямой к оси абсцисс равен половине ширины запрещенной зоны: (tgj = – Eg/2), т.е. численно равен энергии активации.
Подвижность носителей в собственном полупроводнике, где нет никаких примесей и дефектов, определяется рассеянием носителей на фононах. Поскольку средняя длина свободного пробега электрона обратно пропорциональна концентрации фононов, которая, в свою очередь, в области высоких температур пропорциональна температуре, то un ~ 1/T. При низких температурах подвижность носителей практически не зависит от температуры. Таким образом, электропроводность собственных полупроводников изменяется от температуры по экспоненциальному закону (9.1).

Примесная проводимость. Примеси и дефекты в полупроводниках делят на доноры и акцепторы. Доноры отдают в объем полупроводника избыточные электроны и создают электронную проводимость (n-типа). Акцепторы захватывают валентные электроны вещества, в результате чего создаются дырки и возникает дырочная проводимость (р-типа). Наличие в полупроводниках примесных атомов и структурных дефектов обусловливает существование в запрещенной зоне локальных разрешенных энергетических состояний – примесных уровней.
Если в полупроводник введена донорная или акцепторная примесь, то при низких температурах, когда энергии тепловых колебаний недостаточно для переброса электронов из валентной зоны в зону проводимости, свободные носители заряда могут появиться за счет ионизации примесей или дефектов. Энергия ионизации мелких доноров и акцепторов незначительна по сравнению с шириной запрещенной зоны полупроводника, поэтому связанный с донорным атомом электрон может быть оторван от этого атома, т.е. переведен с донорного уровня в зону проводимости (рис. 9.3, а). Чем выше температура, тем больше доноров отдают свои электроны. Правда, с повышением температуры увеличивается и вероятность межзонных переходов. Поэтому количество электронов в зоне проводимости полупроводника, содержащего доноры, может значительно превышать количество дырок в валентной зоне, и электропроводность будет электронной. Такой полупроводник называют электронным (донорным) или полупроводником n-типа. Электроны являются в нем основными носителями заряда, а дырки – неосновными.
В полупроводнике, содержащем акцепторную примесь, электроны легко переходят из валентной зоны на акцепторные уровни, а в валентной зоне образуются дырки (рис. 9.3, б). Их количество значительно больше, чем количество свободных электронов, образовавшихся за счет переходов из валентной зоны в зону проводимости. Поэтому дырки являются основными носителями заряда, а электроны – неосновными. Проводимость полупроводника, содержащего акцепторную примесь, будет дырочной, а сам полупроводник в соответствии с этим называется дырочным (акцепторным) или полупроводником р-типа.

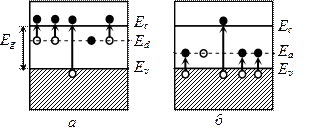
Положение примесных уровней в запрещенной зоне полупроводника определяется энергией ионизации атомов примесей. В качестве примера рассмотрим элементарные полупроводники IV группы таблицы Менделеева – Ge и Si. Донорные примесные уровни в них создают элементы V группы (P, As, Sb, Bi), а акцепторные уровни – элементы III группы (B, Al, Ga, In).
Предположим, что в одном из кристаллов германия находится атом мышьяка (As), имеющий пять электронов в валентной оболочке. Четыре валентных электрона участвуют в образовании ковалентных связей с четырьмя атомами германия. Поскольку ковалентная связь является насыщенной, пятый электрон новую связь образовывать не может. Он сравнительно слабо взаимодействует с большим числом окружающих мышьяк атомов германия, вследствие чего его связь с атомом мышьяка уменьшается и он движется по орбите большого радиуса (рис. 9.4, а). Его движение можно сравнить с движением электрона в атоме водорода. Таким образом, задача определения энергии ионизации примесного атома сводится к отысканию уровней энергии водородоподобного атома. При ее решении необходимо учесть следующие обстоятельства.
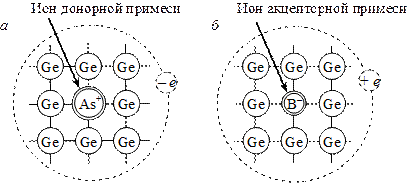
Рис. 9.4 Схема кристаллической структуры германия с атомом
донорной (а) и акцепторной (б) примеси
Поскольку электрон движется не только в кулоновском поле иона As+, но и в периодическом поле кристаллической решетки полупроводника, он обладает эффективной массой mэ. Взаимодействие электрона с ионом мышьяка, имеющим заряд Z×e (Z – кратность заряженного иона), происходит в твердом теле с диэлектрической проницаемостью e. В этом случае решение уравнения Шрёдингера для пятого электрона мышьяка дает собственные значения энергии этого электрона (в эВ):
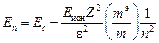 . (9.5)
. (9.5)
Здесь энергия отсчитывается от дна зоны проводимости Ec; 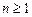 – квантовое число; Eион = 13,52 эВ – энергия ионизации атома водорода.
– квантовое число; Eион = 13,52 эВ – энергия ионизации атома водорода.
Энергия ионизации примесного атома Ed (рис. 9.3, а) равна по абсолютному значению энергии основного состояния электрона (n = 1):
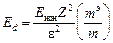 . (9.6)
. (9.6)
Из формулы (9.6) следует, что: 1) Ed значительно меньше энергии ионизации атома водорода; 2) Ed растет с увеличением Z, поэтому уровень двукратно заряженного иона примеси лежит в запрещенной зоне полупроводника ниже уровня однократно заряженного иона.
Расчетное значение энергии ионизации примесных атомов в кристалле германия ( 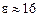 , mэ = 0,25 m) составляет
, mэ = 0,25 m) составляет 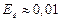 эВ, в кристалле кремния – ~0,04 эВ. Таким образом, достаточно совсем незначительной энергии, чтобы перевести пятый электрон мышьяка из связанного состояния в свободное, т.е. в зону проводимости. Экспериментально определенные значения энергии ионизации доноров в германии и кремнии (табл. 9.2) достаточно хорошо согласуются с расчетными величинами Ed.
эВ, в кристалле кремния – ~0,04 эВ. Таким образом, достаточно совсем незначительной энергии, чтобы перевести пятый электрон мышьяка из связанного состояния в свободное, т.е. в зону проводимости. Экспериментально определенные значения энергии ионизации доноров в германии и кремнии (табл. 9.2) достаточно хорошо согласуются с расчетными величинами Ed.
Таблица 9.2 Энергия ионизации доноров
в кремнии и германии
| Донор | Ed, эВ | |
| в Si | в Ge | |
| P | 0,045 | 0,0128 |
| As | 0,053 | 0,0140 |
| Sb | 0,043 | 0,0098 |
| Bi | 0,069 | 0,0125 |
Пользуясь моделью водородоподобного атома, можно оценить размеры области, в которой локализована волновая функция электрона, связанного с примесным атомом:
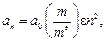 (9.7)
(9.7)
где а0 = 0,53×10-10 м – радиус первой боровской орбиты атома водорода. Для донорной примеси в германии получаем а1 = 64а0 » 34×10-10 м. Поскольку постоянная решетки германия равна примерно 0,56 нм, первая боровская орбита электрона примесного атома охватывает около 200 узлов решетки. Радиус первой боровской орбиты электрона примеси V группы в кремнии несколько меньше, однако тоже достаточно велик (а1 » 30 а0).
Положение акцепторных уровней в запрещенной зоне полупроводника оценивают аналогичным образом. Предположим, что один из узлов решетки германия замещен примесным атомом III группы таблицы Менделеева, например, атом бора (рис. 9.4, б). Три валентных электрона атома бора образуют три ковалентные связи с соседними атомами германия, а четвертая связь остается незавершенной. Она представляет собой дырку с положительным зарядом +е, что обеспечивает электронейтральность области кристалла, окружающей примесь. Атом бора может захватить незавершенной связью электрон основного вещества и превратиться в отрицательно заряженный ион.
Собственные значения энергии для акцепторной примеси можно вычислить таким же путем, каким их определяют для донорной примеси:
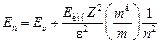 , (9.8)
, (9.8)
где mд – эффективная масса дырки. Основной уровень акцепторной примеси (n = 1)
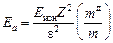 (9.9)
(9.9)
находится в запрещенной зоне германия примерно на 0,01 эВ выше потолка валентной зоны. В табл. 9.3 приведены экспериментальные значения Ea примесей III группы в германии и кремнии, отсчитанные от потолка валентной зоны.
Из формул (9.5) и (9.8) следует, что наряду с основными примесными уровнями в запрещенной зоне могут существовать возбужденные примесные состояния, соответствующие значениям квантового числа n = 2, 3, 4,¼ Они расположены выше основного донорного состояния или ниже основного акцепторного (рис. 9.5). Экспериментально такие состояния были обнаружены в запрещенной зоне кремния при температуре жидкого гелия. Однако при обычных температурах возбужденные состояния можно не учитывать, т.к. из-за малой величины Ed и Ea они не оказывают существенного влияния на электрические свойства полупроводников.
Таблица 9.3 Энергия ионизации акцепторов
в кремнии и германии
| Акцептор | Ea, эВ | |
| в Si | в Ge | |
| B | 0,045 | 0,0104 |
| Al | 0,057 | 0,0102 |
| Ga | 0,065 | 0,0108 |
| In | 0,016 | 0,0102 |
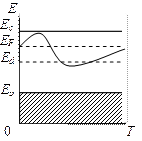
В электронном полупроводнике, содержащем донорную примесь с концентрацией Nd, при Т = 0 К уровень Ферми EF лежит посередине между дном зоны проводимости и примесным уровнем. С ростом температуры уровень Ферми смещается: сначала он приближается к зоне проводимости, а затем начинает опускаться в запрещенную зону (рис. 9.6). Это снижение приводит к тому, что концентрация электронов в зоне проводимости увеличивается. Постепенно концентрация n электронов в зоне проводимости становится сравнимой с Nd. Равенство n = Nd означает, что вся донорная примесь ионизована. Область температур, в которой выполняется это равенство, называется областью истощения примеси. Полная ионизация примеси наступает, когда ЕF опускается на несколько kT ниже Ed.

| 
| |
| Рис. 9.5 Основные и возбужденные примесные состояния в запрещен-ной зоне полупроводника | Рис. 9.6 Положение уровня Ферми в донорном полупроводнике в зависимости от температуры |
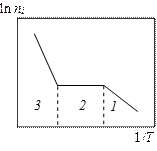
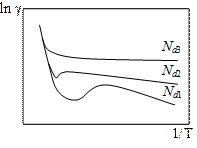
Дальнейшее повышение температуры вызывает увеличение концентрации электронов в зоне проводимости за счет переходов в нее электронов из валентной зоны. Температурная зависимость концентрации электронов приведена на рис 9.7. В области высоких температур (область 3) она такая же, как у собственных полупроводников (см. рис. 9.2).
| 
| |
| Рис. 9.7 Зависимость концентрации электронов от температуры в донорном полупроводнике: 1 – ионизация примесей; 2 – область истощения примесей; 3 – переходы электронов из валентной зоны в зону проводимости | Рис. 9.8 Зависимость удельной электропроводности примесного полупроводника от температуры при концентрациях донорных примесей Nd1 < Nd2 < Nd3 |
В примесных полупроводниках подвижность носителей заряда ограничена рассеянием не только на фононах, но и на ионизованных атомах примесей. При высоких температурах доминирует рассеяние на фононах. Подвижность, обусловленная рассеянием на ионизованной примеси, u ~ T 3/2.
Таким образом, температурная зависимость электропроводности примесного полупроводника немонотонна: в интервале температур, где концентрация носителей экспоненциально зависит от температуры, g(Т) также практически является экспоненциальной функцией, а в области истощения примесей ход кривой g(Т) определяется температурной зависимостью подвижности носителей. Типичный вид температурной зависимости электропроводности примесного полупроводника с разной концентрацией донорных примесей Ndi показан на рис. 9.8.
9.3 Контактные явления
Контактные явления в полупроводниках – это неравновесные электронные процессы, возникающие при прохождении электрического тока: 1) через контакт полупроводника с металлом или другим полупроводником (гетеропереход) либо 2) через границу двух областей одного и того же полупроводника, отличающихся типом носителей заряда (p–n-переход) или разной их концентрацией. Контакты полупроводника с металлом или другим полупроводником обладают выпрямляющим свойством, т.е. значительно эффективнее пропускают электрический ток в одном направлении, чем в обратном. Это свойство обусловило их широкое применение в технике.
Электронно-дырочныйилиp-n-переход – переходная область между двумя соприкасающимися одинаковыми полупроводниками, один из которых имеет электронную, а другой – дырочную проводимость. Концентрация дырок в р-области гораздо выше, чем в n-области, поэтому дырки из р-области диффундируют в n-область, а электроны из n-области – в р-область. В результате в р-области остаются отрицательно заряженные акцепторные атомы, а в n-области – положительно заряженные донорные атомы. Так как, и те и другие неподвижны, в области p-n-перехода образуется двойной слой пространственного заряда: отрицательные заряды в р-области и положительные – в n-области (рис. 9.9, а). Возникающее поле Ек двойного электрического слоя препятствует дальнейшей диффузии основных носителей тока. Поле Eк обусловливает контактную разность потенциалов:
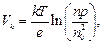
где е – заряд электрона, Т – температура полупроводника, n и p – концентрации электронов и дырок в n- и p-областях, n0 – концентрация электронов в собственном полупроводнике.
При определенной толщине двойного электрического слоя наступает равновесное состояние контакта, характеризуемое выравниванием уровня Ферми EF для обоих полупроводников (рис. 9.9, в). В области p-n-перехода энергетические зоны искривляются, в результате чего возникают потенциальные барьеры eVк как для электронов, так и для дырок. Толщина d слоя p-n-перехода в полупроводниках составляет 10–6–10–7 м, а контактная разность потенциалов Vк – десятые доли вольт. При обычных температурах носители тока не способны преодолеть потенциальный барьер eVк, поэтому контактный слой является запирающим, т.е. характеризуется повышенным сопротивлением.

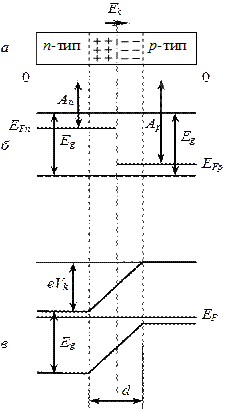
Внешнее электрическое поле изменяет высоту потенциального барьера eVк и нарушает равновесие потоков носителей тока через барьер. Внешнее поле, направление которого совпадает с полем Ек контактного слоя (рис. 9.10, а), вызывает движение электронов в n-полупроводнике и дырок в p-полупроводнике от границы p-n-перехода в противоположные стороны. В результате запирающий слой расширится и его сопротивление возрастет. Такое направление внешнего поля называют запирающим (обратным). В запирающем направлении электрический ток через p-n-переход практически не проходит.
Внешнее электрическое поле, приложенное к p-n-переходу, противоположно полю контактного слоя (рис. 9.10, б) и вызывает движение электронов и дырок к границе p-n-перехода навстречу друг другу. В области перехода носители рекомбинируют, толщина и сопротивление контактного слоя его уменьшаются. При таком направлении внешнего поля электрический ток проходит сквозь p-n-переход от p- к n-полупроводнику. В результате p-n-переход приобретает одностороннюю проводимость, а направление приложенного поля называют пропускным или прямым.
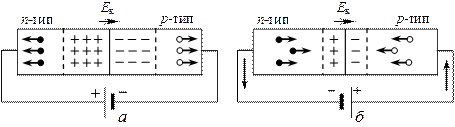
Рис. 9.10 Электронно-дырочный переход во внешнем электрическом поле:
а – запирающее направление; б – пропускное направление
Зависимость тока, протекающего через p-n-переход, от приложенного напряжения (вольтамперная характеристика) обладает резко выраженной нелинейностью (рис. 9.11). При изменении знака U значение тока через p-n-переход изменяется в 105–106 раз. Благодаря этому электронно-дырочный переход является вентильным элементом, используемым в полупроводниковых диодах для выпрямления переменного тока.
Гетеропереход – контакт двух разных по химическому составу полупроводников. На границе гетероперехода происходит изменение свойств полупроводникового материала: структуры энергетических зон, ширины запрещенной зоны, эффективных масс носителей заряда, их подвижности и т.д. Гетеропереход называют изотипным, если он образован полупроводниками с одинаковым типом проводимости, и анизотипным, если механизмы проводимости контактирующих полупроводников разные.
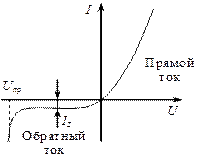
Рис. 9.11 Вольтамперная характеристика p-n-перехода: IS – ток насыщения; Uпр – напряжение пробоя
Наибольшее практическое значение имеют гетеропереходы, образованные монокристаллами. Для получения идеальных монокристаллических гетеропереходов (без дефектов кристаллической решетки и поверхностных состояний на границе раздела полупроводников) необходимо, чтобы у полупроводников совпадали коэффициенты термического расширения, типы и периоды кристаллических решеток. Для получения гетеропереходов, близких к идеальным, периоды решеток полупроводников должны совпадать с точностью до ~ 0,1 %. В зависимости от способа получения гетероперехода толщина d переходной области между двумя однородными полупроводниками может колебаться в широких пределах. В наиболее «резких» гетеропереходах d » 20 Å, т.е. равна толщине 4÷5 атомных слоев. Комбинации различных гетеропереходов образуют гетероструктуры.
Механизм протекания тока в гетеропереходах обусловлен различием в высотах потенциальных барьеров для электронов и дырок. При, так называемом прямом смещении (см. p-n-переход), на анизотипном гетеропереходе не одинаковы как потоки носителей между полупроводниками с разной шириной запрещенной зоны, так и токи инжектированных электронов и дырок. Поэтому в гетеропереходах обычно происходит односторонняя инжекция носителей из широкозонного полупроводника (эмиттера) в узкозонный.
В электронной технике широко применяют гетеропереходы между полупроводниковыми монокристаллами типа AIIIBV, например, на основе арсенида галлия. Гетероструктуры получают также на основе многокомпонентных твердых растворов, период решетки которых не изменяется при изменении состава раствора в широких пределах. Изготавливают гетероструктуры методами эпитаксиального наращивания полупроводниковых кристаллов. Гетеропереходы используются в полупроводниковых приборах: транзисторах, тиристорах, гетеролазерах, светодиодах, фотодетекторах и др.
Дата добавления: 2014-12-04; просмотров: 4964;
