Дональдс Вудс Винникот
В тех случаях, когда нет жестких требований к качеству управления движением исполнительных органов рабочей машины, используются более простые привода, состоящие из силового выключателя и электродвигателя.
С точки зрения способов распределения механической энергии разнообразные ЭП можно разделить на 3 вида: групповой, индивидуальный, взаимосвязанный.
Групповой ЭП применялся на первых этапах развития техники привода и обеспечивал движение исполнительных органов нескольких рабочих машин или нескольких исполнительных органов одной и той же машины. Передача механической энергии и ее распределение в этом случае осуществлялось от одного двигателя с помощью трансмиссий. Очевидные недостатки такого привода – громоздкость механических связей, сложность управления движением каждого исполнительного органа. Вследствие этого групповой ЭП в настоящее время почти не применяется..
В индивидуальном ЭП управление движением каждого исполнительного органа обеспечивается отдельным двигателем, что упрощает механические передачи, облегчает управление движением, позволяет достичь более высоких энергетических показателей.
Взаимосвязанный ЭП имеет два или несколько электрически или механически связанных между собой двигателей. Примером взаимосвязанного ЭП может служить привод цепного конвейера большой протяженности. Исполнительным органом такого конвейера служит цепь, приводимая в движение несколькими двигателями, установленными по длине конвейера. Взаимосвязанный ЭП широко применяется в транспортных установках, бумагоделательных машинах, текстильных агрегатах, прокатных станах металлургического производства и т.д. Одной из разновидностей взаимосвязанного ЭП является многодвигательный привод – это электропривод, в котором несколько двигателей работают на общий вал.
Приведение моментов и сил сопротивления, инерционных масс и моментов инерции
В большинстве случаев, как отмечалось выше, двигатель приводит в движение исполнительный орган механизма через механическое передаточное устройство, отдельные элементы которого движутся с различными скоростями.
При инженерных расчетах в большинстве практических случаев можно принять механические связи абсолютно жесткими (не учитывать упругость звеньев и наличие зазоров в передачах). Тогда движение одного элемента дает полную информацию о движении всех остальных элементов, и достаточно рассматривать один элемент. В качестве такого элемента обычно принимают вал двигателя. В результате расчетную схему механической части привода можно свести к одному обобщенному механическому звену. В качестве него обычно принимают вал двигателя.
При этом возникает задача определения эквивалентного (приведенного) момента инерции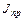 
и момента сопротивления 
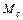(статического момента) производственного механизма.
Для приведения к валу двигателя момента или усилия нагрузки исполнительного органа производственного механизма используется уравнение энергетического баланса системы. Мощность на валу двигателя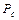 
определяется мощностью статического сопротивления 
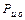на исполнительном органе и потерями 
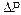в механических звеньях
= 
+ 
.
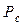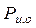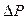Потери мощности можно учесть введением в расчеты соответствующего КПД кинематической схемы
= 
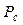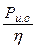. (2.1)
Для механизма с вращательным движением исполнительного органа (см. рис. 2.2) мощность, Вт определяется общим соотношением
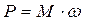, (2.2)
где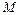 
- момент на соответствующем звене, Н×м;
w - угловая скорость этого звена, рад/с.
Отметим, что угловая скорость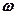 
, рад/с связана с частотой вращенияn, об/мин соотношением
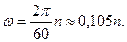
Обозначим через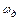 
угловую скорость вала двигателя, wио - угловую скорость вала исполнительного органа, а соответствующие моменты - Мс и Мио. С учетом (2.1), (2.2.) можно записать
,
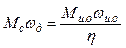откуда момент сопротивления механизма, приведенный к валу двигателя
.
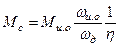Или учитывая, что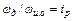 
есть передаточное отношение редуктора, получим
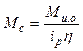(2.3)
 |
В установившихся режимах момент Мс уравновешивается моментом двигателя М (см. рис. 2.2, 2.3).
При поступательном движении исполнительного органа (см. рис. 2.3)
,
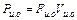где Fи.o – усилие нагрузки на исполнительном органе, Н;
Vи.o – линейная скорость его движения, м/с.
Тогда с учетом (2.1) получим
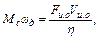
откуда
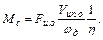
Отношение линейной скорости исполнительного механизма к угловой скорости двигателя
Vи.o/wд = r
имеет размерность метры и называется радиусом приведения нагрузки к валу двигателя. Используя это понятие последнее выражение можно переписать в виде
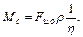
Приведение моментов инерции к одной оси вращения основывается на равенстве кинетических энергий переходной и эквивалентной (приведенной) системы. В эквивалентной системе инерционность всех видов звеньев реальной механической системы заменяется одним моментом инерции Jпр, приведенным к валу двигателя. при наличии вращающихся частей с моментом инерции J1, J2...Jn и угловыми скоростями w1, w2,...wn (см. рис. 2.2) с учетом баланса кинетических энергий можно записать:
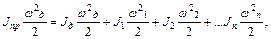
откуда
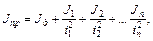(2.4)
где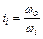 
- передаточное отношение редуктора от вала двигателя до i-го элемента; 
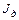- момент инерции двигателя и других элементов (муфты, шестерни и т.п.), установленных на валу двигателя.
Часто в каталогах для двигателей указывается величина махового момента GD2, кгс×м. В этом случае момент инерции в системе СИ вычисляется по формуле
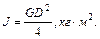
Если в кинематической схеме имеются поступательно движущиеся элементы (см. рис. 2.3), то их масса приводится к валу двигателя также на основе равенства запаса кинетической энергии
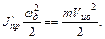
Откуда дополнительная составляющая момента инерции, приведенная к валу двигателя
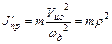. (2.5)
Если механизм имеет вращающиеся и поступательно-движущиеся элементы, то выражение (1.4) содержит дополнительно слагаемые вида (1.5).
Лекция 23-24 Механика электропривода
При проектировании электропривода электродвигатель должен выбираться так, чтобы его механические характеристики соответствовали механическим характеристикам производственного механизма. Механические характеристики дают взаимосвязь переменных в установившихся режимах.
Механической характеристикой механизма называют зависимость между угловой скоростью и моментом сопротивления механизма, приведенными к валу двигателя) w=f(Mс.
Среди всего многообразия выделяют несколько характерных типов механических характеристик механизмов:
1. Характеристика с моментом сопротивления, не зависящим от скорости (прямая 1 на рис. 2.4). Такой характеристикой обладают, например, подъемные краны, лебедки, поршневые насосы при неизменной высоте подачи и др.
2. Характеристика с моментом сопротивления линейно зависящим от скорости (прямая 2 на рис. 2.4). Такая зависимость присуща, например, приводу генератора постоянного тока с независимым возбуждением, работающему на постоянную нагрузку.
3. Характеристика с нелинейным возрастанием момента (кривая 3 на рис. 2.4.). Типичными примерами здесь могут служить характеристики вентиляторов, центробежных насосов, гребных винтов. Для этих механизмов момент Мс зависит от квадрата угловой скорости w.
4. Характеристика с нелинейно спадающим моментом сопротивления (кривая 4 на рис. 2.4). Например, у механизмов главного движения некоторых металлорежущих станков моментМсизменяется обратно пропорционально w, а мощность потребляемая механизмом, остается постоянной.
 |
Механической характеристикой электродвигателя называется зависимость его угловой скорости от вращающего момента wд = f(M).
В качестве примеров на рис. 2.5 приведены механические характеристики: 1 - синхронного двигателя; 2 – двигателя постоянного тока независимого возбуждения; 3 – двигателя постоянного тока последовательного возбуждения.
Для оценки свойств механических характеристик электропривода используют понятие жесткости характеристики. Жесткость определяется по выражению
,
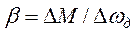где DМ – изменение момента двигателя;
Dwд – соответствующее изменение угловой скорости.
Для линейных характеристик значение b остается постоянным, для нелинейных – зависит от рабочей точки.
Используя это понятие, характеристики, приведенные на рис. 2.5, можно качественно оценить так: 1 – абсолютно жесткая (b = ¥); 2 – жесткая; 3 – мягкая.
Уравнение движения электропривода. Статическая устойчивость электропривода.
При воздействии на электропривод различных возмущений (изменение статического момента, колебания сетевого напряжения и т.п.) в нем возникают переходные процессы. Уравнение движения электропривода учитывает силы и моменты, действующие в переходных режимах.
Как известно из физики в соответствии с законом Ньютона при поступательном движении движущая сила F уравновешивается силой сопротивления Fcмашины и инерционной силой 
.
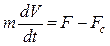Для электропривода характерно вращательное движение, а уравнение его движения имеет аналогичный вид
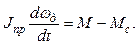(2.6)
Здесь аналогом массы является приведенный момент инерции Jпр , вместо линейной скорости V рассматривается угловая скорость wд, а в правую часть уравнения входят момент двигателя Ми статический момент механизма Мс. Из уравнения (2.6) следует, что в установившемся режиме, когда ускорение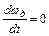 
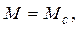(2.7)
т.е. момент двигателя уравновешивается моментом сопротивления производственного механизма.
На рис. 2.6 показаны механические характеристики: 1 – двигателя и 2 – производственного механизма. (Фактически момент двигателя и момент Мс имеют противоположные знаки, но для удобства анализа их показывают в одном и том же квадрате). Очевидно, что равенству (2.7) соответствует на рис. 2.6 точка а, где характеристики пересекаются. При этом угловая скорость электропривода равна wд1.
Установившийся режим работы привода может быть устойчивым или неустойчивым. Для решения этого вопроса проанализируем поведение электропривода при отключениях от равновесного режима в точке а.
Предположим под действием возмущения угловая скорость отклонилась относительно wдна +Dw . В этом случае момент двигателя уменьшается и примет значение М1 (см. рис 2.6), а статический момент возрастет до Мс1,т.е будет иметь место соотношение
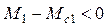
При этом, в соответствии с уравнением (2.6), ускорение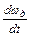 
будет отрицательным, т.е. привод будет замедляться, а w д снижаться. Система стремится возвратиться к положению равновесия в точку а, что условно показано на рис. 2.6 стрелками.
 |
Рассмотрим теперь ситуацию, когда угловая скорость отклоняется на - Dw: момент двигателя возрастает до М2, а момент механизма снижается до Мс2, и выполняется соотношени
.
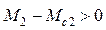Ускорение 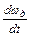в этом случае будет положительным, угловая скорость wдвозрастает, и система вновь стремится к положению равновесия в точке а.
Проведенный анализ показывает, что режим работы электропривода в точке а для рассматриваемого сочетания характеристик двигателя и механизма будет устойчивым.
Условие устойчивости является совершенно необходимым условием работоспособности электропривода. Следует учитывать, что оно выполняется далеко не всегда. Предлагается самостоятельно провести аналогичный анализ для сочетания характеристик, показанных на рис. 2.7. (1-характеристика двигателя, 2- характеристика механизма), и убедиться, что в точке а условия устойчивости выполняются, а в точке в нет.
Выводы, получаемые в результате проведенного анализа, характеризуют, так называемую статическую устойчивость электропривода, т.е. способность системы возвращаться к исходному режиму при достаточно «малых» отклонениях.
Диапазон регулирования скорости. Статические ошибки.
Многие производственные механизмы, например, механизмы подачи и главного движения металлорежущих станков, механизмы подъемно-транспортных установок и др. требуют регулирования скорости исполнительных органов. Для таких механизмов используются регулируемые электроприводы.
Важнейшими показателями качества для регулируемого электропривода являются диапазон регулирования скорости и падение скорости от нагрузки.
Под диапазоном регулирования скорости понимают отношение верхней (наибольшей) скорости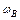 
к нижней 
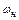(наименьшей скорости. Под верхней и нижней скоростями обычно понимают задаваемые значения угловых скоростей на холостом ходу (см. рис. 2.8)
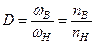. (2.8)
Например, если электропривод имеет верхнюю скорость 
=1000об/мин и D =1000, то нижняя скорость 
обмин.
Падение скорости под нагрузкой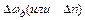 
(см. рис.2.8) определяют обычно при номинальном значении нагрузки (момента). Величину 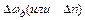называют также абсолютной статической ошибкой от нагрузки. Для оценки качества работы электропривода удобнее использовать значение относительной статической ошибки от нагрузки.
Относительная ошибка определяется обычно в процентах по выражению
,
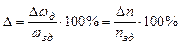где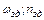 
- заданное значение угловой скорости или частоты вращения.
Значение абсолютной ошибки 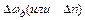на верхней и нижней характеристиках, как правило, одно и то же. При этом относительная ошибка на верхней скорости
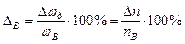, (2.9)
а на нижней
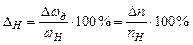(2.10)
Используя выражения (2.9) и (2.10), найдем отношение
.
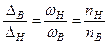Тогда, с учетом выражения (2.9) для диапазона регулирования, получим
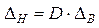. (2.11)
Таким образом, относительная статическая ошибка от нагрузки на нижней скорости в D раз больше, чем на верхней.
Производственные механизмы, как правило, требуют поддержания скорости с заданной точностью во всем диапазоне регулирования. Отсюда следует, что при проектировании электропривода нужно прежде всего обеспечить требуемую точность стабилизации на нижней скорости.
Лекция 25-27 Энергетика электропривода
Основное назначение электропривода – преобразовывать электрическую энергию в механическую и управлять этим процессом. В связи с этим энергетические показатели и характеристики электропривода имеют первостепенное значение, тем более, что электропривод потребляет около 60-65% электроэнергии, производимой в стране.
Любой процесс передачи и преобразования энергии сопровождается ее потерями, т.е. входная мощность Рвх всегда больше выходной Рвых на величину потерь ∆Р, и очень важно, сколь велики эти потери.
Энергетическую эффективность процесса в данный момент обычно оценивают посредством коэффициента полезного действия (КПД), определяемого как
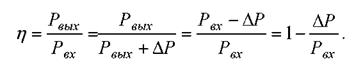(6.1)
Важными энергетическими характеристиками изделия – двигателя, преобразователя, редуктора или электропривода в целом – служит номинальный КПД
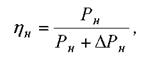(6.2)
где Рн , ∆Рн - номинальная выходная мощность и номинальные потери, и зависимость КПД от относительной нагрузки η = f(P/Pн); для регулируемого электропривода часто удобно использовать зависимости η= f(ω) при заданном моменте.
В случаях, когда в линии, питающей электропривод, напряжение и ток не совпадают по фазе и имеют несинусоидальную форму, используется еще одна энергетическая характеристика - коэффициент мощности, определяемый как
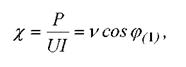(6.3)
где Р - активная мощность;
v= I/I(1) - коэффициент искажений;
U, I, I(1)- действующие значения напряжения, тока, первой гармоники тока;
φ(1) - угол сдвига между первыми гармониками напряжения и тока. При небольших искажениях v ≈ 1, т.е.
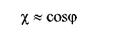(6.4)
При передаче по линии с некоторым активным сопротивлением Rл активной мощности Р при cos φ ≠ 1потери ∆Р≈ вырастут в сравнении с потерями при передачи той же мощности постоянным током ∆Р= в отношении
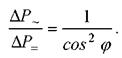
Оценки энергетической эффективности электропривода вида (6.1) справедливы, как отмечалось, лишь, если процесс неизменен во времени. Если же нагрузка заметно меняется во времени, следует пользоваться оценками, определяемыми по энергиям за время t
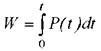
и
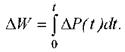
Для циклических процессов с однонаправленным потоком энергии и временем цикла удобным и информативным показателем служит цикловой КПД, определяемый как
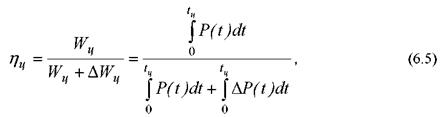
где Wц и ∆Wц- полезная энергия и потери энергии за цикл
Оценка энергетической эффективности при неоднонаправленных потоках энергии
Изложенное выше относилось к однонаправленным потокам энергии, когда мощность не меняет знак. Вместе с тем, часто встречаются случаи, когда направление потока энергии в цикле изменяется: подъем - спуск, разгон - торможение и т.п. Здесь приведенная выше формула КПД (6.5) становится недостаточной - неочевидно понятие «полезной энергии», интегрирование знакопеременных мощностей лишено смысла. Устранить неопределенность можно, условившись о равноправности всех режимов в цикле, если они необходимы для осуществления технологического процесса и, следовательно, полезны. Так, тормозной режим в транспортном средстве ничем не хуже режима разгона. Удержание руки робота в нужном месте какое-либо время - тоже очень полезное действие.
Если принять, что разнополярный график P(t) полезен, то естественно перейти к определению полезной энергии W в(6.5) по следующему выражению:
Для энергетического канала (рис. 6.1), состоящего из источника электроэнергии, передающих и преобразовательных звеньев, рабочего органа, указывается место оценки - между i-м и (i+1)-м звеньями, а также те звенья - от k-ого го до l-ого, в которых учитываются потери. Тогда с учетом (6.5) показатель энергетической эффективности - обобщенный КПД - имеет вид:
где
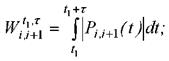
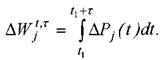
Верхний индекс указывает временной интервал - от t1 до τ, на котором производится оценка
Рис. 6. 1. Энергетический канал электропривода
Из (6.7) получаются выражения (6.1) и (6.5), однако обобщенный показатель может дать значительно большую информацию. Например, если выбрать местом оценки сечение 0,1 и учесть потери во всех элементах от 1 до n, то при Р0,1 > 0 получим оценку эффективности потребления энергии на интервале τ. Оценка будет работать и при Wn-1,n = 0, т.е. при отсутствии электромеханического преобразования энергии. При оценке в сечении n-1,n отразит эффективность преобразования энергии, т.е. меру потерь, которыми сопровождается полезная механическая работа, и т.п.
Обобщенный показатель удобен для сравнения по энергетическому критерию различных систем, выполняющих одинаковые функции при относительно сложных режимах работы.
Потери в установившихся режимах
Потери в электрических машинах детально изучаются в соответствующих курсах Основные составляющие потерь в машине:
Общее представление об энергетической эффективности нерегулируемого электропривода дает зависимость КПД двигателя с редуктором от относительной нагрузки. На рис. 6.3 для ориентировки приведена такая зависимость для двигателей средней мощности (15-150 кВт) с хорошим редуктором (КПД больше 0,95).
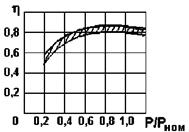
Рис. 6.3. Типичная зависимость КПД от нагрузки
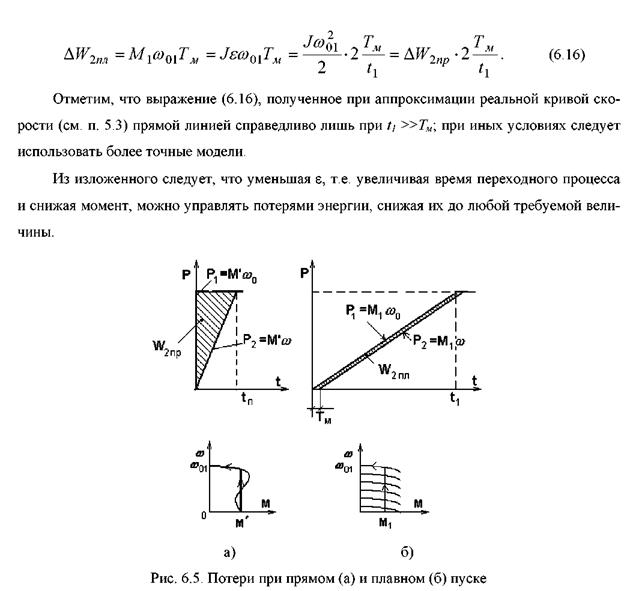
Необходимо подчеркнуть, что работа с недогрузкой приводит к заметному снижению КПД, поэтому неоправданное завышение мощности двигателя «на всякий случай» - вредно. Так же вредны в соответствии с (6.5) неудачно организованные циклы, когда холостой ход занимает в цикле большое место.
В регулируемом по скорости электроприводе энергетическая эффективность определяется главным образом выбранным способом регулирования, в связи, с чем все способы можно разделить на две большие группы в зависимости от того, изменяется или нет ωо в процессе регулирования.
К первой группе ωо = const относятся все виды реостатного регулирования, а также регулирование асинхронного двигателя с к.з. ротором изменением напряжения при неизменной частоте. Если принять для простоты, что Рэм ≈ P1 и ∆Р2 ≈ ∆Р2м, то для этой группы получим:
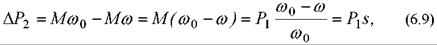
т.е. потери в роторной (якорной) цепи при любой нагрузке пропорциональны разности скоростей ∆ω(ωо - ω) или скольжению
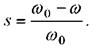
При реостатном регулировании лишь часть этих потерь, пропорциональная
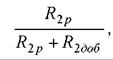
рассеивается внутри машины и греет ее. Другая часть, пропорциональная
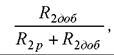
рассеивается вне машины, ухудшая, разумеется, энергетические показатели электропривода. Именно эта часть в каскадных схемах используется полезно.
Сложнее и неприятнее соотношение (6.9) проявляется в асинхронном электроприводе с к.з. ротором при регулировании изменением напряжения или каким-либо еще «хитрым» способом, но при постоянной частоте. Здесь вся мощность ∆Р2 = P1sрассеивается в двигателе, нагревая его и делая способ практически непригодным для продолжительного режима работы.
Интересно, что соотношение (6.9) нельзя «обмануть», хотя такие попытки делались и еще делаются.
К второй группе ωо = var относятся все «безреостатные» способы регулирования в электроприводах постоянного тока - изменением напряжения и магнитного потока и частотное регулирование в электроприводах переменного тока.
Принципиально способы второй группы энергетически предпочтительны, поскольку в (6.9) разность скоростей ∆ωо ≈ const, однако следует учитывать, что в устройствах, обеспечивающих ωо = var, тоже есть потери и при малых мощностях, небольших диапазонах регулирования и немалой стоимости устройств необходимы детальные сопоставления.
Потери в переходных режимах
Как было показано ранее (п. 5.2), переходные процессы при быстрых изменениях воздействующего фактора могут сопровождаться большими бросками момента и тока, т.е. значительными потерями энергии. Поставим задачу оценить величину потерь энергии в переходных процессах и найти связи между потерями и параметрами электропривода. Будем учитывать только потери в активных сопротивлениях силовых цепей двигателя, так как именно эта составляющая общих потерь заметно возрастает в переходных процессах.
Анализ проведем лишь для переходных процессов, отнесенных ранее к первым двум группам (п.п. 5.2 и 5.3) и начнем с важного частного случая, когда фактор, вызывающий переходный прогресс, изменяется мгновенно, а процесс протекает в соответствии со статическими характеристиками (п. 5.2).
Потери энергии в цепи ротора или якоря за время переходного процесса tnn определяются с учетом (6.9) как
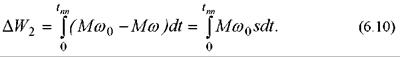
Для переходного процесса вхолостую (Мс = 0) будем иметь:
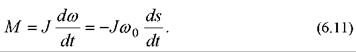
Подставив (6.11) в (6.10) и сменив пределы интегрирования, получим:
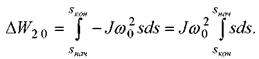
После интегрирования получим окончательно
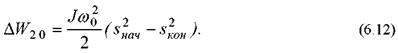
Энергосбережение средствами электропривода
Громадная доля электроэнергии, потребляемая электроприводом, – до 65% в развитых странах, и осуществление электроприводом практически всех технологических процессов, связанных с движением, делают особенно актуальной проблему энергосбережения в электроприводе и средствами электропривода. В мировой практике к настоящему времени сформировалось несколько основных направлений, по которым интенсивно ведутся исследования, разработки, осуществляются крупные промышленные проекты.
1. В нерегулируемом электроприводе, реализованном на основе асинхронных электродвигателей с к.з. ротором, много внимания уделяется так называемым энергоэффективным двигателям, в которых за счет увеличения массы активных материалов, их качества, а также за счет специальных приемов проектирования удается поднять на 1–2% (мощные двигатели) или на 4-5% (небольшие двигатели) номинальный КПД при некотором увеличении цены двигателя.
Этот подход, используемый и активно рекламируемый с 70-х годов сначала в США, затем в Европе, может приносить пользу, если технологический процесс действительно не требует регулирования скорости, если нагрузка меняется мало и если двигатель правильно выбран. Во всех других случаях использование более дорогих энергоэффективных двигателей может оказаться нецелесообразным.
2. Правильный выбор двигателя для конкретного технологического процесса – один из важнейших путей энергосбережения. В европейской практике принято считать, что средняя загрузка двигателей составляет 0,6, тогда как в нашей стране, где до недавнего времени не было принято экономить ресурсы, этот коэффициент составляет 0,3 – 0,4, т.е. привод работает с КПД значительно ниже номинального. Завышенная «на всякий случай» мощность двигателя часто приводит к незаметным на первый взгляд, но очень существенным отрицательным последствиям в обслуживаемой электроприводом технологической сфере, – например, к излишнему напору в гидравлических сетях, связанному с ростом потерь и снижением надежности и т.п.
3. Основной путь энергосбережения средствами электропривода – подача конечному потребителю – технологической машине – необходимой в каждый момент мощности. Это может быть достигнуто посредством управления координатами электропривода, т.е. за счет перехода от нерегулируемого электропривода к регулируемому. Этот процесс стал в последние годы основным в развитии электропривода в связи с появлением доступных технических средств для его осуществления – преобразователей частоты и т.п.
4. Выбор рациональных в конкретных условиях типов электропривода и способов управления, обеспечивающих минимизацию потерь в силовом канале, – важный элемент в общей проблеме энергосбережения.
Ожидается, что переход от нерегулируемого электропривода к регулируемому в технологиях, где это требуется, может сэкономить до 25-30% электроэнергии. В одной из технологий – в водо - воздухоснабжении – переход к регулируемому электроприводу, как показал опыт, экономит около 50% электроэнергии, до 25% воды и до 10% тепла.
Дональдс Вудс Винникот
Дата добавления: 2014-12-03; просмотров: 878;