Целые числа со знаком

Обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком:
прямой код, обратный код, дополнительный код

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде.

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

1. Прямой код.
В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины.
2. Обратный код.
Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями.
3. Дополнительный код.
Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные чисел

целочисленные данные во внутреннем представлении занимают 2 байта; диапазон возможных значений – от -32768 до +32767 (2¹⁵); данные представляются точно.

вещественные данные занимают 6 байт; диапазон возможных значений модуля от 2.9E-39 до 1.7E+38; точность представления данных – 11..12 значащих цифр.

символ занимает 1 байт.

логический тип занимает 1 байт и имеет два значения: FALSE(ложь) и TRUE(истина).

Вещественные числа. ……

Для кодирования вещественных чисел существует специальный формат чисел с плавающей запятой. Число при этом представляется в виде:

где M - мантисса^[1],

p - порядок числа N,

q - основание системы счисления.

Если при этом мантисса M удовлетворяет условию

то число N называют нормализованным.

Мантисса и порядок числа при записи его в ячейке памяти представляются определенными группами битов. Два разряда отводятся под знаки мантиссы (числа) и порядка.

Примеры:

49. Количество информации в слове «Информатика» при условии, что для кодирования используется 32-значный алфавит, равно _______ битам(-ов).

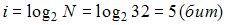Решение: Количество информации, которое вмещает один символ N-элементного алфавита, равно Это известная формула Р. Хартли. В 32-значном алфавите каждый символ несет информации. В слове «Информатика» 11 символов. Количество информации в слове «Информатика» при кодировании в 32-значном алфавите равно

Сколько разрядов (бит) нужно для записи чисел?????

0 0

1 =2⁰ 0+1=1 бит 1

2 =2¹ 1+1=2 бит 10 1+1ноль

3 11

4 =2² 2+1=3 бит 100 1+2нуля

5 101

6 110

7 111

8 =2³ 3+1=4 бит 1000 1+3нуля

9 1001

10 1010

11 1011

12 1100

13 1101

14 1110

15 1111

16 =2⁴ 4+1=5 бит 10000 1+4нуля

1)Число байт, необходимое для записи числа 2⁸²:
5 ;10; 11; 82; 256.

Число 2⁸² в двоичной форме представляется как единица и 82 нуля, то есть занимает 1+82=83 бита. Байт равен 8 битам, и для записи потребуется 11 байт = 88 бит (ближайшее целое число байт справа).

Ответ: 11 байт

2)Число байт, необходимое для записи числа 4¹²:
5 ;10; 11; 82; 256.

4¹²=(2²)¹²=1+24=25бит; 25:8=4байт; Ответ: 4 байт

Объем видеопамяти, необходимой для хранения битовой карты изображения разрешением 1024 х 768 точек в режиме «true color» (16777216 = 2²⁴ цветов), больше, чем в режиме 256 цветов при разрешении экрана 1280 х 1024 точки, на _____ Мбайт

.Решение

1. Количество бит на точку (пиксель) режима «true color» равно

Рассчитаем объем видеопамяти для хранения битовой карты 1024 х 768 точек.

2. Аналогично для режима 256 цветов.

3. Объем видеопамяти в первом случае больше

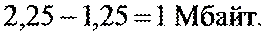на 1Mб
Ответ: 1.