Оценка трудоемкости поиска в случайном дереве
Обозначим значения ключей, следующих в порядке возрастания k1,k2,…,kn. Вероятность того, что в корень попадет ключ ki, равна 1/n. Тогда в левом поддереве будет i-1 узлов, а в правом n-i узлов. Пусть an – средний
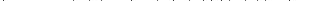 |
уровень узла в дереве, содержащем n узлов. Тогда при условии, что ключ ki находится в корне,
Выражение в правой части содержит три слагаемых:
1. искомый узел находится в левом поддереве с вероятностью (i-1)/n и средний уровень его равен ai-1+1
2. с вероятностью 1/n это корень и его уровень 1.
3. с вероятностью (n-i)/n искомый узел находится в правом поддереве и средний уровень его an-i+1
 Искомая величина an представляет собой среднее по i для всех
Искомая величина an представляет собой среднее по i для всех 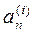
(1)
Отсюда следует: 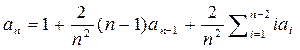 (2)
(2)
а из (1) можно получить: 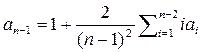 (3)
(3)
Из (3) можно найти 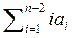 , и, подставив это в (2), получим:
, и, подставив это в (2), получим:
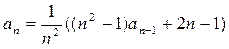 (4)
(4)
an можно представить в виде: 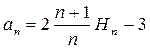 (5),где
(5),где 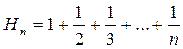 . Справедливость (5) можно проверить непосредственной подстановкой (5) в (4).
. Справедливость (5) можно проверить непосредственной подстановкой (5) в (4).
По формуле Эйлера 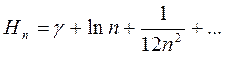 , где
, где 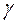 - постоянная Эйлера, равная 0.571… Для больших n получим:
- постоянная Эйлера, равная 0.571… Для больших n получим:
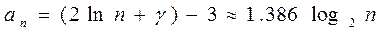
В заключение отметим, что, хотя среднее время поиска в случайном дереве пропорционально логарифму числа узлов, тем не менее, существует досадная
 |
возможность получения вырожденного дерева, время поиска в котором пропорционально числу узлов. Примеры таких деревьев приведены на рис.42.
Рис.42 Примеры вырожденных деревьев
Дата добавления: 2014-12-02; просмотров: 1157;
