Сбалансированные деревья
Сбалансированные деревья представляют собой компромисс между оптимальными и случайными деревьями. Авторы идеи сбалансированного дерева - Адельсон-Вельский и Ландис (1962 г.), поэтому такие деревья называют также AVL-деревьями. AVL-деревья используют дополнительно 2 бита на узел и позволяют за время ~log2N, выполнять операции вставки, поиска и удаления.
Определим высоту дерева как максимальную длину пути от корня до листа. Будем называть дерево сбалансированным, если в каждом узле высота
 |
правого и левого поддеревьев различаются не более чем на ±1. На рис. 43
Рис.43 Пример сбалансированного дерева
изображен пример сбалансированного дерева. Оценим максимальную высоту сбалансированного дерева. Обозначим минимальное число узлов в AVL-дереве высоты h через N(h). В таком дереве с минимальным числом узлов одна из ветвей, исходящих из корня, должна содержать N(h-1) узлов, а другая - N(h-2) узлов. Таким образом,
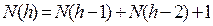 (6)
(6)
Очевидно, что N(0)=1, N(1)=2. Далее по формуле (6) находим , что N(2)=4. Для h=3 и h=4 можно непосредственно проверить, а затем по индукции доказать, что при h³3 справедливо неравенство
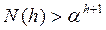 (7)
(7)
где
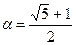 -положительный корень уравнения
-положительный корень уравнения 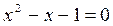 , которое является характеристическим для разностного уравнения (6). Действительно, допустим, что неравенство (7) выполняется для всех k<N. Тогда, подставив в правую часть равенства (6) нижние границы N(h-1), N(h-2) в соответствии с неравенством (7), получим:
, которое является характеристическим для разностного уравнения (6). Действительно, допустим, что неравенство (7) выполняется для всех k<N. Тогда, подставив в правую часть равенства (6) нижние границы N(h-1), N(h-2) в соответствии с неравенством (7), получим:
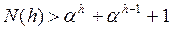 (8)
(8)
Подставим в левую часть неравенства (7) нижнюю грань для N(h) из неравенства (8). В результате будет получено более сильное неравенство:
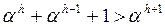 (9)
(9)
Очевидно, что если (9) справедливо, то тем более справедливо (7). Преобразуем неравенство (9) к виду:

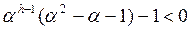
Трехчлен в скобках тождественно равен нулю, так как a - его корень. Остается –1<0. Таким образом, неравенство (7) доказано. Следовательно, если сбалансированное дерево содержит ветвь длины h>3, то число его вершин n удовлетворяет неравенству 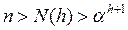 , откуда
, откуда
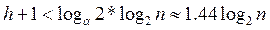 (10)
(10)
Величина h+1 – это число сравнений ключей при поиске записи, расположенной в конце пути длиной h, исходящем из корня. Окончательный вывод: число сравнений ключей при поиске в сбалансированном дереве из n узлов не превышает 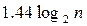 .
.
Дата добавления: 2014-12-02; просмотров: 1290;
