НОРМАЛЬНЫЕ АЛГОРИТМЫ
Каждый нормальный алгоритм (НА) является определенным процессом преобразования слов в некотором конечном алфавите и задается набором допустимых элементарных преобразований и правилами, определяющими порядок применения этих преобразований. При этом в качестве элементарного преобразования используется замена одного вхождения подслова в слове некоторым другим (или тем же словом). Всевозможные замены для заданного НА определяются его схемой, а последовательность проведения замен – схемой и некоторыми дополнительными соглашениями. Эти соглашения одни и те же для всех НА, а потому НА, по существу, однозначно определяются алфавитом и схемой.
Определение 1. Схемой нормального алгоритма 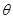 в алфавите
в алфавите

называется упорядоченная последовательность
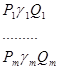 (1)
(1)
слов  в алфавите
в алфавите  где
где 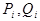 - слова в алфавите
- слова в алфавите 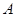 , а
, а 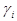 есть слово
есть слово 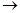 или
или 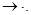 При этом слово
При этом слово  схемы (1) называется ее
схемы (1) называется ее 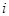 -й формулой с левой частью
-й формулой с левой частью 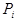 и правой частью
и правой частью  .
.
Формула  называется простой, если
называется простой, если 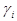 есть
есть 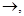 и заключительной, если есть
и заключительной, если есть 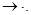
Действие НА 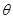 на слово
на слово 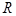 в алфавите
в алфавите 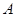 описывается следующим определением.
описывается следующим определением.
Определение 2. Пусть 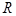 - слово в алфавите
- слово в алфавите 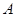 и хотя бы одно из слов
и хотя бы одно из слов 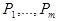 является его подсловом. Элементарным преобразованием слова
является его подсловом. Элементарным преобразованием слова 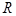 по нормальному алгоритму
по нормальному алгоритму 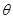 со схемой (1) называется замена в
со схемой (1) называется замена в 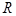 первого вхождения слова
первого вхождения слова 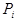 с наименьшим номером
с наименьшим номером 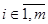 словом
словом  Если результатом указанного элементарного преобразования является слово
Если результатом указанного элементарного преобразования является слово 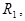 то пишут
то пишут  т. е.
т. е.  или
или  .
.
Определение 3. Говорят, что НА 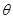 в алфавите
в алфавите 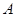 применим к слову
применим к слову 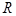 в алфавите
в алфавите 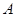 и перерабатывает его в слово
и перерабатывает его в слово 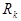 , если существует конечная последовательность слов
, если существует конечная последовательность слов
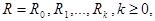 (2)
(2) 
в которой



 или
или 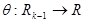 и слово
и слово 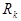 не содержит подслов
не содержит подслов 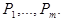
В противном случае говорят, что алгоритм 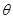 не применим к слову
не применим к слову 
Из приведенных определений естественным образом извлекается описание процесса переработки слова 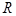 по нормальному алгоритму
по нормальному алгоритму 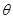 (или нормальным алгоритмом
(или нормальным алгоритмом 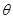 ). А именно, по заданному слову
). А именно, по заданному слову 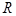 НА
НА 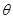 строит последовательность слов. Если
строит последовательность слов. Если 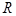 не содержит подслов
не содержит подслов  то эта последовательность одноэлементна и состоит из единственного слова
то эта последовательность одноэлементна и состоит из единственного слова 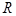 . Если же
. Если же 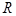 содержит хотя бы одно из подслов
содержит хотя бы одно из подслов 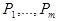 , то производится его элементарное преобразование по НА
, то производится его элементарное преобразование по НА 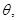 в результате чего получается вполне определенное слово
в результате чего получается вполне определенное слово 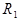 . Если при переходе от
. Если при переходе от 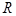 к
к 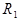 использовалась заключительная формула, то искомая последовательность двухэлементная:
использовалась заключительная формула, то искомая последовательность двухэлементная: 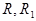 . В противном случае так же, как и выше, по слову
. В противном случае так же, как и выше, по слову 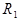 строится слово
строится слово  и т. д. В процессе построения указанной последовательности могут представиться три различные возможности: или на каком-то шаге будет использована заключительная формула схемы алгоритма, или появится слово, не содержащее подслов
и т. д. В процессе построения указанной последовательности могут представиться три различные возможности: или на каком-то шаге будет использована заключительная формула схемы алгоритма, или появится слово, не содержащее подслов 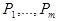 , или не произойдет ни того, ни другого. В превых двух случаях мы получим конечную последовательность, последнее слово которой называется результатом применения НА к слову
, или не произойдет ни того, ни другого. В превых двух случаях мы получим конечную последовательность, последнее слово которой называется результатом применения НА к слову 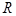 и обозначают через
и обозначают через 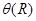 . В третьем случае процесс преобразования слов по НА
. В третьем случае процесс преобразования слов по НА 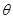 будет длитться бесконечно, это и означает, что НА
будет длитться бесконечно, это и означает, что НА 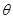 не применим к
не применим к 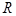 .
.
Таким образом, НА 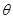 в алфавите
в алфавите 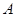 задает частичное отображение множества
задает частичное отображение множества 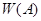 всех слов в алфавите
всех слов в алфавите 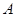 в само себя. Выбирая различные схемы, мы будем получать различные НА.
в само себя. Выбирая различные схемы, мы будем получать различные НА.
Если 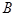 - алфавит, содержащий
- алфавит, содержащий 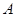 , то НА в алфавите
, то НА в алфавите 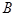 называется нормальным алгоритмом над алфавитом
называется нормальным алгоритмом над алфавитом 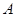 .
.
Приведем примеры нормальных алгоритмов. При этом буквой 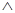 будет всегда обозначаться пустое слово (в любом алфавите).
будет всегда обозначаться пустое слово (в любом алфавите).
1. НА в алфавите 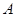 со схемой
со схемой

перерабатывает любое слово 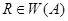 в себя, причем последовательность слов, соответствующая слову
в себя, причем последовательность слов, соответствующая слову  имеет вид:
имеет вид: 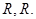 .
.
2. НА со схемой
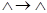
не применим ни к одному слову. Последовательность, соответствующая слову 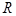 будет бесконечной:
будет бесконечной:

3. НА 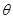 в алфавите
в алфавите 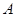 со схемой
со схемой

приписывает к любому слову 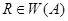 слева слово
слева слово  :
:
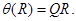
4. Построим НА 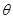 , приписывающий к любому слову
, приписывающий к любому слову 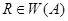 справа фиксированное непустое слово
справа фиксированное непустое слово  Это сделать несколько сложнее, чем приписывание слова
Это сделать несколько сложнее, чем приписывание слова  слева. Для этого удобнее расширить алфавит
слева. Для этого удобнее расширить алфавит 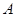 , добавив к нему одну новую букву
, добавив к нему одну новую букву  , и построить искомый НА в алфавите
, и построить искомый НА в алфавите 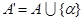 (т. е. над
(т. е. над 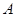 ). Нетрудно проверить, что нужное нам преобразование будет осуществлять НА со схемой
). Нетрудно проверить, что нужное нам преобразование будет осуществлять НА со схемой


……………..
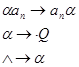
Последовательность слов, соответствующая произвольному слову 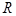 в алфавите
в алфавите 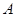 , для этого НА имеет вид:
, для этого НА имеет вид:
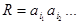
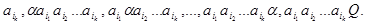
Очевидно, что то же самое преобразование слов будет осущетвлять НА, полученный из 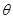 любой перестановкой
любой перестановкой 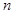 формул его схемы. В связи сэтим вместо первых
формул его схемы. В связи сэтим вместо первых 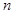 формул схемы пишут просто
формул схемы пишут просто
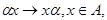
так, что вся схема запишется в виде:

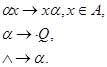
Заметим, что, выполняя свою задачу приписывания к словам из 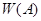 справа слова
справа слова  , мы совсем не интересовались переработкой слов в алфавите
, мы совсем не интересовались переработкой слов в алфавите 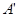 , содержащих букву
, содержащих букву  . Здесь алгоритм
. Здесь алгоритм 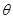 будет действовать иначе. А именно, слово
будет действовать иначе. А именно, слово 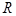 в алфавите
в алфавите 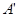 , содержащее
, содержащее  вхождений буквы
вхождений буквы  , он будет перерабатывать в слово
, он будет перерабатывать в слово
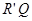
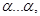 где количество букв
где количество букв  будет равно
будет равно 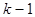 ,
,
где 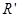 получается из
получается из 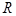 удалением всех вхождений буквы
удалением всех вхождений буквы  (т. е.
(т. е. 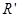 есть проекция
есть проекция 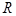 в алфавит
в алфавит 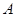 ).
).
5. Построим НА 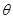 , перерабатывающий любое слово
, перерабатывающий любое слово 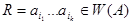 в перевернутое слово
в перевернутое слово  Для этого добавим к
Для этого добавим к 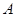 две новые буквы
две новые буквы 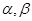 и возьмем следующую схему
и возьмем следующую схему 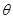 в алфавите
в алфавите 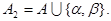

Проследите в качестве упражнения, что 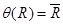 для любого слова
для любого слова 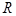 в алфавите
в алфавите 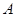 .
.
Приведем еще примеры НА над числами. Условимся натуральное число 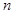 записывать в виде
записывать в виде 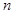 вертикальных палочек.
вертикальных палочек.
6. НА в алфавите  со схемой
со схемой

осуществляет сложение натуральных чисел.
7. НА в алфавите 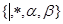 со схемой
со схемой

осуществляет умножение натуральных чисел.
Дата добавления: 2014-12-02; просмотров: 1189;
