Тема 10. РЯДЫ

Задание 29. С помощью признаков сравнения исследовать на сходимость нижеприведенные ряды.

29.1.	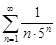.	29.2.	.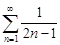
29.3.	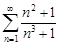.	29.4.	.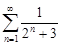
29.5.	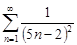.	29.6.	.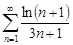
29.7.	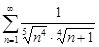.	29.8.	.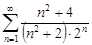
29.9.	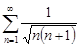.	29.10.	.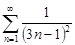
29.11.	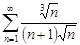.	29.12.	.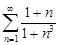
29.13.	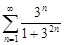.	29.14.	.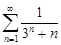
29.15.	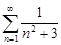.	29.16.	.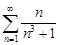
29.17.	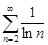.	29.18.	.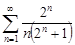
29.19.	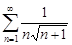.	29.20.	.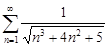
29.21.	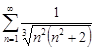.	29.22.	.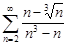
29.23.	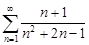.	29.24.	.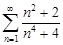
29.25.	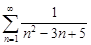.	29.26.	.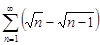
29.27.	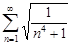.	29.28.	.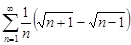
29.29.	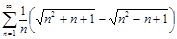.	29.30.	.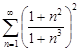

Задание 30.С помощью признака Даламбера исследовать на сходимость нижеприведенные ряды.

30.1.	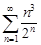.	30.2.	.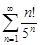
30.3.	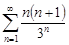.	30.4.	.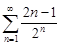
30.5.	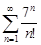.	30.6.	.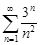
30.7.	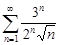.	30.8.	.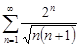
30.9.	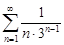.	30.10.	.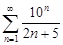
30.11.	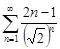.	30.12.	.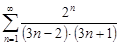
30.13.	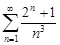.	30.14.	.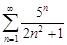
30.15.	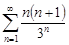.	30.16.	.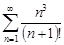
30.17.	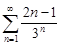.	30.18.	.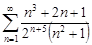
30.19.	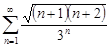.	30.20.	.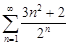
30.21.	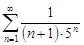.	30.22.	.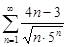
30.23.	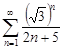.	30.24.	.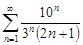
30.25.	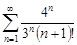.	30.26.	.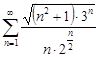
30.27.	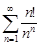.	30.28.	.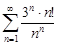
30.29.	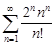.	30.30.	.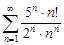

Задание 31.С помощью признака Коши исследовать на сходимость нижеприведенные ряды.

31.1.	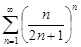.	31.2.	.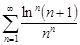
31.3.	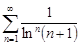.	31.4.	.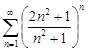
31.5.	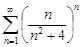.	31.6.	.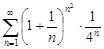
31.7.	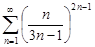.	31.8.	.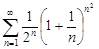
31.9.	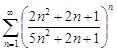.	31.10.	.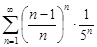
31.11.	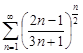.	31.12.	.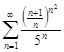
31.13.	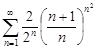.	31.14.	.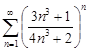
31.15.	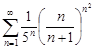.	31.16.	.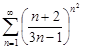
31.17.	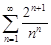.	31.18.	.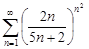
31.19.	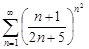.	31.20.	.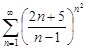
31.21.	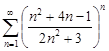.	31.22.	.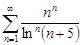
31.23.	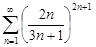.	31.24.	.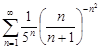
31.25.	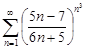.	31.26.	.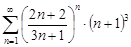
31.27.	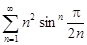.	31.28.	.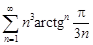
31.29.	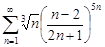.	31.30.	.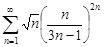

Задание 32.Исследовать на сходимость нижеприведенные ряды с помощью интегрального признака Коши.

32.1.	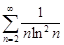.	32.2.	.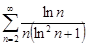
32.3.	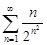.	32.4.	.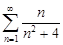
32.5.	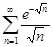.	32.6.	.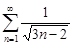
32.7.	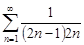.	32.8.	.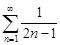
32.9.	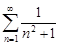.	32.10.	.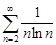
32.11.	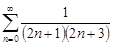.	32.12.	.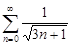
32.13.	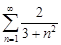.	32.14.	.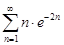
32.15.	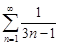.	32.16.	.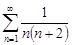
32.17.	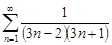.	32.18.	.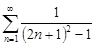
32.19.	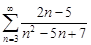.	32.20.	.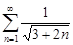
32.21.	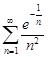.	32.22.	.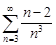
32.23.	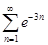.	32.24.	.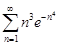
32.25.	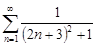.	32.26.	.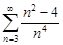
32.27.	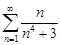.	32.28.	.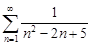
32.29.	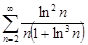.	32.30.	.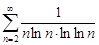

Задание 33.Указать сходящиеся абсолютно, сходящиеся условно и расходящиеся ряды.

33.1.	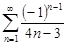.	33.2.	.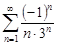
33.3.	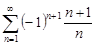.	33.4.	.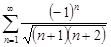
33.5.	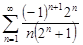.	33.6.	.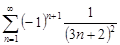
33.7.	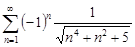.	33.8.	.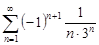
33.9.	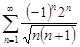.	33.10.	.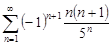
33.11.	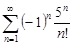.	33.12.	.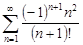
33.13.	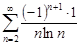.	33.14.	.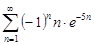
33.15.	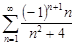.	33.16.	.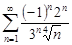
33.17.	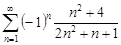.	33.18.	.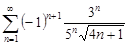
33.19.	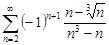.	33.20.	.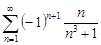
33.21.	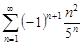.	33.22.	.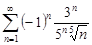
33.23.	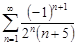.	33.24.	.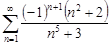
33.25.	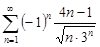.	33.26.	.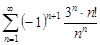
33.27.	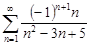.	33.28.	.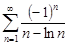
33.29.	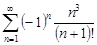.	33.30.	.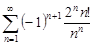

Задание 34.Исследовать сходимость степенного ряда.

34.1.	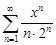.	34.2.	.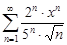
34.3.	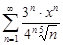.	34.4.	.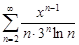
34.5.	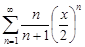.	34.6.	.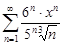
34.7.	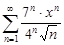.	34.8.	.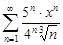
34.9.	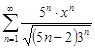.	34.10.	.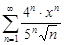
34.11.	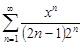.	34.12.	.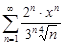
34.13.	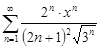.	34.14.	.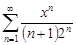
34.15.	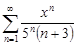.	34.16.	.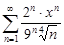
34.17.	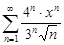.	34.18.	.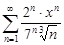
34.19.	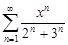.	34.20.	.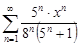
34.21.	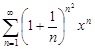.	34.22.	.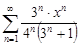
34.23.	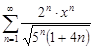.	34.24.	.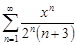
34.25.	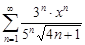.	34.26.	.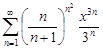
34.27.	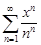.	34.28.	.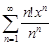
34.29.	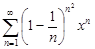.	34.30.	.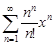

Задание 35.Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подинтегральной функции в степенной ряд и почленного интегрирования этого ряда.

35.1.	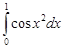.	35.2.	.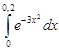
35.3.	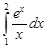.	35.4.	.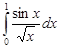
35.5.	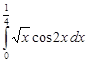.	35.6.	.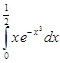
35.7.	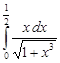.	35.8.	.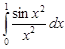
35.9.	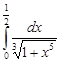.	35.10.	.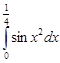
35.11.	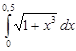.	35.12.	.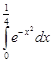
35.13.	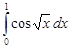.	35.14.	.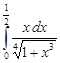
35.15.	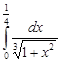.	35.16.	.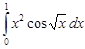
35.17.	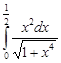.	35.18.	.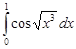
35.19.	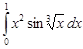.	35.20.	.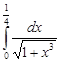
35.21.	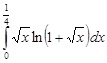.	35.22.	.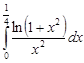
35.23.	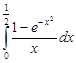.	35.24.	.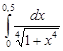
35.25.	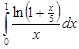.	35.26.	.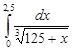
35.27.	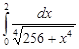.	35.28.	.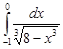
35.29.	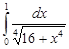.	35.30.	.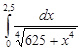

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Высшая математика. Общий курс : учеб. для вузов / А. В. Кузнецов [и др.] ; под ред. А. И. Яблонского. – Минск : Выш. шк., 1993. – 349 с.

Гусак, А. А. Высшая математика : учеб. пособие для вузов. В 2 т. Т. 1 / А. А. Гусак. – Минск : ТетраСистемс, 1998. – 544 с.

Гусак, А. А. Задачи и упражнения по высшей математике : учеб. пособие для вузов. В 2 ч. Ч. 1 / А. А. Гусак. – Минск : Выш. шк., 1988. – 246 с.

Гусак, А. А. Справочник по высшей математике : учеб. для вузов / А. А. Гусак, Г. М. Гусак, Е. А. Бричкова. – Минск : ТетраСистемс, 2000. – 640 с.

Данко, П. Е. Высшая математика в упражнениях и задачах : учеб. пособие для вузов. В 2 ч. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М. : Оникс, 2002. – 304 с.

Карасев, А. И. Курс высшей математики для экономических вузов : учеб. пособие для студентов экон. специальностей вузов. В 2 ч. Ч. 1 / А. И. Карасев, З. М. Аксютина, Т. И. Савельева. – М. : Высш. шк., 1982. – 272 с.

Красс, М. С. Математика для экономических специальностей : учеб. для вузов / М. С. Красс. – М. : Дело, 2002. – 704 с.

Кудрявцев, В. А. Краткий курс высшей математики : учеб. пособие / В. А. Кудрявцев, Б. П. Демидович. – М. : Наука, 1989. – 656 с.

Марков, Л. Н. Высшая математика : учеб. пособие для вузов. В 2 ч. Ч. 1 / Л. Н. Марков, Г. П. Размыслович. – Минск : Амалфея, 1999. – 208 с.

Минорский, В. П.Сборник задач по высшей математике : учеб. пособие / В. П. Минорский. – М. : Наука, 1987. – 349 с.

Минюк, С. А. Высшая математика : учеб. пособие для вузов /
С. А. Минюк, Е. А. Ровба. – Гродно : ГрГУ, 2000. – 394 с.

Практикум по высшей математике для экономистов : учеб. пособие для вузов / под ред. Н. Ш. Кремера. – М. : ЮНИТИ-ДАНА, 2004. – 423 с.

Сборник задач и упражнений по высшей математике. Общий курс : учеб. пособие / А. В. Кузнецов [и др.]. – Минск : Выш. шк., 1994. – 284 с.

Сборник индивидуальных заданий по высшей математике : учеб. пособие для вузов. В 3 ч. Ч. 1 / А. П. Рябушко [и др.] ; под ред.
А. П. Рябушко. – Минск : Выш. шк., 1990. – 269 с.

Шипачев, В. С. Высшая математика : учеб. для немат. специальностей вузов / В. С. Шипачев ; под ред. А. Н. Тихонова. – М. : Высш. шк., 1990. – 479 с.

Шипачев, В. С. Высшая математика : учеб. для вузов / В. С. Шипачев. – М. : Высш. шк., 1998. – 479 с.

СОДЕРЖАНИЕ

Пояснительная записка..................................................................... 3

Тема 1. Векторная алгебра............................................................... 4

Тема 2. Матрицы и определители.................................................... 8

Тема 3. Решение систем линейных уравнений.............................. 11

Тема 4. Геометрия пространства Rⁿ............................................... 13

Тема 5. Предел функции................................................................. 19

Тема 6. Дифференциальное исчисление функций
одной переменной........................................................................... 29

Тема 7. Функции двух переменных................................................ 32

Тема 8. Интегральное исчисление и его применение................... 35

Тема 9. Дифференциальные уравнения.......................................... 48

Тема 10. Ряды.................................................................................. 53

Список рекомендуемой литературы.............................................. 62

Учебное издание