Портфеля (модель Марковица), модель оценки

капитальных активов (модель Шарпа)

Модель Марковица. Существует бесконечное число портфелей, доступных для инвестора, но в тоже время инвестор должен рассматривать только те портфели, которые принадлежат к эффективному множеству. Однако эффективное множество Марковица представляет собой изогнутую линию, что предполагает наличие бесконечного числа точек на ней (рисунок 22.1).

Согласно трактовке Марковица, если имеется некий портфель А, то он является неэффективным, так как портфель В мог бы обеспечить тот же самый уровень ожидаемой доходности с меньшей степенью риска, в то врем как портфель С при той же степени риска мог бы обеспечить более высокую ожидаемую доходность. Все эффективные портфели лежат на прямой EF, которая называется «эффективной границей» Марковица. Согласно его теории существует бесконечное количество эффективных портфелей. Перед инвесторами возникает проблема выбора и использования методов определения структуры каждого из бесконечного числа эффективных портфелей.

С целью преодоления данных проблем Марковиц представил метод критических линий. Согласно этому методу для начала инвестор должен оценить вектор ожидаемых доходностей и ковариационную матрицу.

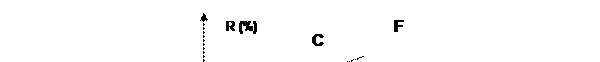
Алгоритм начинается с определения портфеля с наивысшей ожидаемой доходностью (данный портфель является эффективным).

Затем через алгоритм определяется количество «угловых» портфелей, которые связаны с ценными бумагами и полностью описывают эффективное множество. «Угловой» портфель – это эффективный портфель, обладающий следующими свойствами: любая комбинация двух смежных «угловых» портфелей представляет собой третий портфель, лежащий в эффективном множестве между двумя «угловыми» портфелями (портфели, представляющие комбинацию двух несмежных «угловых» портфелей, не будут принадлежать эффективному множеству). Продолжая в том же духе, можно построить несколько десятков эффективных портфелей между вторым и третьим «угловыми» портфелями, а затем соответствующий сегмент эффективного множества. После того как данная процедура будет выполнена для следующего промежутка между третьим и четвертым «угловыми»портфелями, график будет полностью построен.

После того как были определены структура и местоположение эффективного множества Марковица, можно определить состав оптимального портфеля инвестора. Процедура определения состава оптимального портфеля начинается с графического определения инвестором уровня его ожидаемой доходности. То есть из графика инвестор может определить, где располагается портфель, соответствующий точке касания кривых безразличия инвестора с эффективным множеством (О), а затем с помощью линейки отметить его ожидаемую доходность (провести из точки О линию, перпендикулярную вертикальной оси).

Проведя данную операцию, инвестор теперь может определить два «угловых» портфеля с ожидаемыми доходностями, «окружающими» данный уровень. То есть инвестор может определить «угловой» портфель, который имеет ближайшую ожидаемую доходность, большую, чем у данного портфеля (ближайший «угловой» портфель, расположенный «выше» О), и «угловой» портфель с ближайшей, меньшей ожидаемой доходностью (ближайший «угловой» портфель, расположенный «ниже» О).

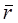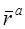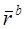Если ожидаемая доходность оптимального портфеля обозначена как и ожидаемые доходности двух ближайших «угловых» портфелей обозначены как и соответственно, тогда состав оптимального портфеля может быть определен с помощью решения следующего уравнения относительно Y:

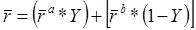(22.1).

Оптимальный портфель будет состоять из доли Y, инвестированной в ближайший «угловой» портфель, находящийся «выше» оптимального, и доли 1-Y, инвестированной в ближайший «угловой» портфель, расположенный «ниже» оптимального.

Если векторы весов ближайших верхних и нижних «угловых» портфелей обозначены X^a и Х^b соответственно, то веса отдельных ценных бумаг, составляющих оптимальный портфель, равняются:

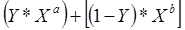(22.2).

Модель Шарпа.Ожидаемую доходность актива можно определить с помощью так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависит от ряда показателей, характеризующих состояние рынка, или индексов.

Простая индексная модель предложена У. Шарпом в середине 60-х гг. Ее часто называют рыночной моделью. В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Она предполагается линейной. Уравнение модели имеет следующий вид:

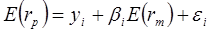(22.3),

где Е(r_i) – ожидаемая доходность актива;

y_i – доходность актива в отсутствие воздействия на него рыночных факторов;

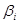– коэффициент 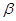актива;

Е(r_m) – ожидаемая доходность рыночного портфеля;

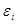– независимая случайная (переменная) ошибка

Независимая случайная ошибка показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней величины равно нулю. Она имеет постоянную дисперсию ковариацию с доходностью рынка, равную нулю; ковариацию с нерыночным компонентом доходности других активов, равную нулю.

Приведенное уравнение является уравнением регрессии. Если его применить к широко диверсифицированному портфелю, то значения случайных переменных ( 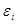) в силу того, что они изменяются как в положительном, так и отрицательном направлении, гасят друг друга, и величина случайной переменной для портфеля в целом стремится к нулю. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь. Тогда модель Шарпа принимает следующий вид:

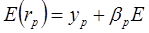(22.4),

где 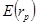– ожидаемая доходность портфеля;

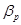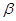– портфеля;

y_p – доходность портфеля в отсутствие воздействия на него рыночных факторов.