Глава 1. ПОЛУЧИТЬ ВСЕ ОТ ЖИЗНИ. Механическая система состоит из двух точечных масс , связанных невесомым стержнем длиной l (рис

Механическая система состоит из двух точечных масс 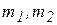, связанных невесомым стержнем длиной l (рис. 3.13). Для исследования движения системы с двумя степенями свободы выбраны две обобщенные координаты – линейная координата x, определяющая положение груза 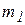, и угловая координата , определяющая угол поворота стержня.

Кинетическая энергия системы:

.

Обобщенные силы: , .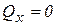

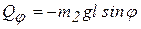Уравнения Лагранжа второго рода (п. 3.11.1) дают два дифференциальных уравнения по каждой из двух обобщенных координат:

.

Эти уравнения полностью описывают движение механической системы. Однако, их решение вызывает определенные математические сложности. Пусть координата 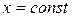, угол является малым, тогда из второго уравнения получается дифференциальное уравнение малых колебаний математического маятника 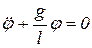. Такое уравнение можно решить как уравнение свободных колебаний материальной точки (п. 3.2.6).

ОСНОВНАЯ УЧЕБНАЯ ЛИТЕРАТУРА

1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: В 2-х томах. Т. 1. Статика и кинематика. – 3-е изд., стереотип. – М.: Наука, 1979. – 272 с. Т. 2. Динамика. – 2-е изд., перераб. и доп. – М.: Наука, 1979. – 544 с. (и другие издания).

2. Гернет М.М. Курс теоретической механики. – 4-е изд., перераб. и сокр. – М.: Высшая школа, 1981. – 304 с. (и другие издания).

3. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики: В 2-х томах. Т. 1. Статика и кинематика. – 8-е изд., перераб. и доп. – М.: Наука, 1982. – 352 с. Т. 2. Динамика. – 6-е изд., перераб. и доп. – М.: Наука, 1983. – 640 с. (и другие издания).

4. Никитин Е.М. Краткий курс теоретической механики. - М.: Наука, 1971. – 400 с. (и другие издания).

5. Тарг С.М. Краткий курс теоретической механики. – 11-е изд., испр. – М.: Высшая школа, 1995. – 416 с. (и другие издания).

6. Яблонский А.А., Никифорова В.М. Курс теоретической механики: В 2-х частях. Ч. 1. Статика и кинематика. – 6-е изд., испр. – М.: Высшая школа, 1984. – 368 с. Ч. 2. Динамика. – 6-е изд., испр. – М.: Высшая школа, 1984. – 412 с. (и другие издания).

Глава 1. ПОЛУЧИТЬ ВСЕ ОТ ЖИЗНИ

Каждый мыслящий человек должен в какой-то момент задать себе вопрос: "Что наиболее ценно для меня в жизни?"

Я хочу процитировать великого комедийного актера Эда Уинна, который весьма мудро заметил: "Богатство и слава - это ерунда, если нет здоровья!"

Что такое больной человек, даже если он знатен и богат? Богатые не могут купить себе счастье. А то, что человек достиг известности, еще не означает, что он стал счастливее.

Я не могу недооценивать богатство. Я считаю, что деньги и положение играют немалую роль в нашей цивилизации. Комфорт я удовольствия важны для многих людей. Заберите у человека все состояние и дайте ему одно здоровье, его первым желанием будет вернуть утерянное богатство. Но когда и то и другое имеется в наличии, остается слово, которое мы боимся произносить, мысль, которую мы гоним от себя, то, что приносит горе, боль и сожаление. Это слово, эта мысль - СМЕРТЬ.

Даже когда жизнь кажется невыносимой ношей, как судорожно человек цепляется за нее! Какие душевные силы тратятся на борьбу со смертью! С какой страстью человек держится за жизнь! Величайшая человеческая мечта - это здоровье и долгая жизнь! Человек чувствует себя в этом мире, как дома, и хотел бы жить здесь вечно, если он здоров и полон молодых сил.