Математика в Древней Греции
Период элементарной математики от VI-V в.в. до н.э. до XVI в.н.э. характеризуется изучением математики постоянных величин. Вклад Древней Греции в науку чрезвычайно велик. Характерная черта греческой математики заключается в переходе от одного предложения к другому с помощью доказательства. В Древней Греции появились первые математические теории.
Из арифметики была выделена теория чисел, наука об общих свойствах операций с натуральными числами. Была разработана теория делимости, рассмотрены арифметические и геометрические прогрессии, отыскивались «пифагоровы тройки» чисел, удовлетворяющих условию: a2 + b2 = c2.
Один из главных результатов греческой математики состоял в открытии несоизмеримости. По теореме Пифагора диагональ a квадрата со стороной, равной единице, удовлетворяет равенству a2 = 12 + 12. Затем греки доказали, что не существует рационального числа, квадрат которого равен 2. Других чисел, кроме рациональных, в математике еще не было.
Греческие математики нашли общие методы решения квадратных уравнений. Ими был развит метод конических сечений, в математику вошли новые линии - гипербола, эллипс, парабола.
Открыв несоизмеримость, греки впервые встретились с противоположностью дискретного и непрерывного. Изучение дискретных предметов привело науку к понятию целого числа. При изучении линии на первый план выступает понятие непрерывности. Противоречия, связанные с непрерывностью и движением, были вскрыты греческими философами.
Первые математические теории побудили ученых систематизировать отдельные факты и изложить последовательно основы математики. В III в. до н.э. были написаны “Начала” Евклида - сочинение, получившее всеобщее признание, логическая строгость которого оставалась непревзойденной в течение двух тысячелетий. “Начала” состоят из 13 книг. В них излагаются основы арифметики, планиметрии и стереометрии.
В арифметике исходным понятием была единица. Число определялось как множество, составленное из единиц.
В геометрию ученые древности ввели три исходные понятия - точку, прямую, плоскость - и сформировали аксиомы и постулаты, т.е. правила, по которым следует обращаться с введенными понятиями. Таким образом, в “Началах” Евклида геометрия построена аксиоматически. В “Началах” пять аксиом и пять постулатов. С помощью этих постулатов обоснованы геометрические построения.
Пятый постулат называется постулатом о параллельных. Еще до Евклида ученые пытались доказать его. Такие попытки предпринимались затем на протяжении двадцати веков, пока в 1826 г. великий русский математик Н.И.Лобачевский не создал свою геометрию, исходя из предположения об изменении пятого постулата Евклида о параллельных. Тем самым была доказана независимость пятого постулата Евклида от остальных предложений.
“Начала” значительно повлияли на развитие математики. В течение многих веков они служили образцом математической строгости. До настоящего времени “Начала” Евклида составляют основу школьного курса геометрии.
Достижения греческой математики не исчерпываются результатами, изложенными в “Началах”. Для удовлетворения потребностей астрономии греки построили геометрию сферы, создали начала тригонометрии. Для определения площадей криволинейных фигур они разработали метод исчерпывания - прообраз будущего интегрального исчисления. Так, Архимед подсчитал площадь сегмента параболы; нашел метод проведения касательных к спирали, который можно считать прообразом дифференциальных методов. Динострат по существу ввел предел 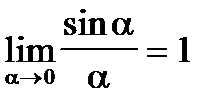 (IV в. до н.э.).
(IV в. до н.э.).
Греческие ученые разработали общую теорию конических сечений. Результаты античной теории конических сечений были использованы математиками XVII в. при создании аналитической геометрии.
Дата добавления: 2014-12-30; просмотров: 2980;
