Интегральные кривые распределения.

Наиболее удобным является графическое отображение дисперсного состава пыли в виде интегральных кривых (Рис. 6). Для построения этих кривых используется для условного сита понятие остатка R(r) или прохода D(r) частиц пыли через отверстие сита. По полученным данным строятся кривые остатков R(r) и кривые прохода D(r), представленные на графике. Эти кривые показывают, какая доля частиц по числу или массе имеет размер R(r) больший или D(r) меньший заданной ве­личины r. Соответственно, получают интегральные кривые распределений по массе или по числу. Эти кривые получаются путем интегрирования функции f(r) и g(r) в пределах от R до бесконечности для кривой остатков и от 0 до R для кривой проходов. Дисперсность может задаваться таблицей остатков или полных проходов частиц разных размеров.

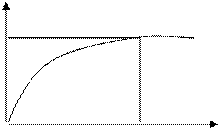D(%)

0 10 100 мкм

Рис 6. Интегральная кривая проходов

где - D(%) - интегральная кривая проходов

Для массового распределения: Для счетного распределения:

R(r) = 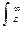g(r)dr - кривая остатков R(r) = 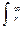f(r)dr

D(r) =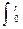g(r)dr, - кривая проходов D(r) = 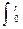f(r)dr,

Суммируя, получим: D(r) + R(r) = 1 Суммируя, получим: D(r) + R(r) = 1

Дисперсность подчиняется общим закономерностям. Для аналитического выражения этих закономерностей используются эмпирические формулы классификации:

R=100e^-bd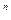

где R – массовое содержание фракции пыли размером больше данного диаметра d;

b и п - постоянные коэффициенты, зависящие от свойств исходного пылеобразующего материала и способа измельчения.

Прологарифмировав ее дважды, получим:

Lg(lg 100/R) = n lg d + C

C = lg B + lg (lg e)

Рис.7. Кривая дисперсности

В системе координат Lg(lg 100/R), lg d кривая дисперсности будет прямой (рис.7), интегральные кривые дисперсности строят в веро­ятно - дисперсной системе координат.

Большинство промышленных пылей подчиняется нормально - логарифмическому закону распределения.

Аналитическое выражение интегральной кривой распределения частиц по размерам:

D(d_ч)=100/(ℓgδr )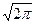

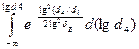
где D(d_ч)-относительное содержание частиц меньше данного размера d_ч,%; D_ч- текущий размер; d_м –медианный размер, при котором число частиц крупнее d_м равно числу частиц мельче d_м; δ_ч – среднее квадратическое отклонение в функции данного распределения.

Эта формула затабулирована. d_м выбирают из условия D(d_ч)=50%, ℓgδ_ч находят по формуле:

ℓgδ_ч=ℓg d_м-ℓg d_15,87=ℓg d_84,13-ℓg d_м

По графику (рис.8) можно получить значение d и dм

d _{84,13 и} d _15,87 – абциссы точек, координаты которых имеют значения 84,13 и 15,87 % соответственно.

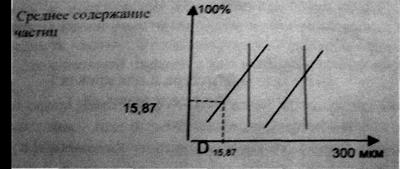
Рис.8. Интегральные кривые дисперсности

Кривые имеют форму прямых, направленных под углом, в зависимости от среднего квадратического отклонения.

Свойство данного распределения:

Если вид этого распределения получен для числа частиц, то он сохраняется и относи­тельно их распределения по массе.

Дисперсный состав является наиболее важ­ным фактором при оценке газопылевых выбросов. От размеров частиц зависят дру­гие свойства частиц, например сыпучесть и слипаемость.