Теплота, температура и механический эквивалент теплоты

Температуру и количество теплоты как различные понятия первым определил Ламберт (1755). В том же году и М. В.Ломоносов указал, что температура тела — степень теплоты — определяется скоростью движения частиц, тогда как количество теплоты зависит от общего количества движения этих частиц, т.е. от их кинетической энергии.

Теплота считалась или веществом, или состоянием еще со времен античности. У философов ионийской школы огонь был четвертым элементом. Тепловые явления рассматривались в разделе «Огонь» и в «Курсе физики» Мушенбрука (1739). Бэкон и Кеплер считали, что теплота есть состояние движения внутренних частей тела. В XVII в. можно было услышать, что термометры измеряют «абсолютное» количество теплоты в теле. Классическая термодинамика родилась в борьбе с теорией теплорода, в которой теплота рассматривалась как неуничтожимая невесомая жидкость, способная перетекать от нагретых тел к более холодным. Но рядом с теорией теплорода возникла кинетическая теория теплоты, твор-

цами которой были Бэкон, Гук, Бойль, Ломоносов, Клаузиус. Термодинамика, возникшая сначала как инженерная дисциплина, имеет целью установление соотношений между параметрами макросистем, не опираясь ни на какие модели строения веществ. Молекулярная физика, наоборот, исследует тепловые явления с микроскопической точки зрения.

Измерение температуры ввели для характеристики степени нагретости тел, но требовались объективные критерии. Исследование тепловых явлений началось после изобретения термометра.

Галилей, Ньютон и другие конструировали термоскопы: тонкая стеклянная трубка, один конец которой заканчивался шариком, а другой, открытый, опускался в сосуд с водой, заполняющей часть трубки. Когда воздух в шарике нагревался (охлаждался), столбик воды в трубке опускался (поднимался). Затем трубки стали снабжать шкалой. Термометр с четкими показателями впервые сделал гданьский стеклодув Г.Д.Фаренгейт: 0 °F — температура смеси воды, поваренной соли и льда, 212 °F — кипения воды, 32 °F — таяния льда, 96 °F — человеческого тела. Эта шкала распространилась с 1714 г., и сейчас принята во многих странах, в том числе в США. Шведский астроном А. Цельсий предложил за 0° взять температуру кипения воды при нормальном давлении, а за 100° — температуру таяния льда (1742). Шведский ботаник К.Линней переставил на шкале Цельсия точки 0 и 100, и появился бытовой термометр с этой шкалой.

Помимо свойства расширения веществ при нагревании, лежащего в основе действия этих термометров, используют изменение электрических свойств с изменением температуры. Термопара состоит из двух проволочек разных металлов (обычно меди и Константина, сплава меди с никелем), спаянных на одном конце, свободные концы присоединены к прибору, измеряющему напряжение. Прибор имеет интервал (от -269 до +2300) °С. Поскольку обычно сопротивление металлов растет при повышении температуры, а в некоторых полупроводниках — падает, то этот эффект тоже используют в очень точных термометрах.

Определение температуры через операцию измерения называется операционным. Для количественного определения нужно найти величину, обладающую свойством температуры — быть одинаковой у всех тел, находящихся в тепловом равновесии. Австрийский физик Л.Больцман установил (1866), что этим свойством обладает средняя кинетическая энергия поступательного движения молекул: 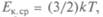где постоянная Больц-мана 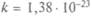Дж/К. Значит, температура — мера средней кинетической энергии поступательного движения молекул идеального газа.

Абсолютная шкала температур, введенная лордом Кельвиным, принята в науке, и потому единица температуры (градус) в этой шкале в системе СИ названа в честь автора и обозначена К. Соотношение температурных шкал показано на рис. 4.1.

К уравнениям теплового баланса пришли петербургские академики Г. Крафт и Г. Рихман, выясняя вопрос о температуре смеси. Рихман открыл, что при смешивании равных количеств воды с разной температурой получается смесь температурой, равной среднему арифметическому начальных температур. Это уравнение вскоре стали называть «задачей Рихмана».

Понятия скрытой теплоты таяния и испарения сформировались на основе этого уравнения и теории теплорода, которую развивал известный французский революционер Ж.Марат. Считали, что теплород содержится в газе, как сок в апельсине, сожмешь апельсин — выдавишь сок, сожмешь газ — выделишь теплород, газ нагреется. Для количественных характеристик нужна единица измерения, ее ввел шведский академик И.К.Вильке (1772). Калория — количество теплоты, соответствующее изменению температуры 1 г воды на 1 °С. Когда Дж. Блэк открыл постоянство точки плавления льда, возникло понятие скрытой теплоты. Калориметр — классический прибор для измерения количества теплоты, используемый и сейчас, сконструировали в 80-е годы XVIII в. Лавуазье и Лаплас, нашедшие удельные теплоемкости многих твердых и жидких тел и их зависимости от температуры. Они отмечали, что «опыты

дают сведения только об отношении количеств теплоты», а не о полном количестве теплоты, и считали природу теплоты иной, не связанной с особым флюидом, теплородом. Они предчувствовали, что наука уйдет от наглядности модели теплорода, и их кинетические взгляды на природу теплоты окажутся более верными. Лавуазье и Лаплас, видимо, первыми поняли физическую сущность понятия теплоемкости.

Работы Л.Эйлера, Д.Бернулли и М.В.Ломоносова показывают, что с точки зрения «корпускулярной философии» можно объяснить различные физические и химические явления, в том числе и тепловые. В работе «Размышления о причине теплоты и стужи» (1745) М.В.Ломоносов исходил из того, что материей и движением определяются все явления природы, что «теплота состоит в некотором движении мельчайших частичек тела».

Понятие теплоемкости ввели для характеристики зависимости количества энергии Q, необходимого для изменения температуры 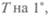от количества вещества, его вида и температуры: с = = 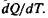Им стали пользоваться Вильке и Блэк к началу XIX в. Так как количество теплоты, необходимое для повышения температуры тела на 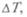пропорционально массе тела 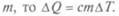Величина с — удельная теплоемкостью вещества. Для воды она максимальна и принята — 1 кал на 1 г на 1 °С.

Открытие Р. Майером эквивалентности теплоты и энергии позволило измерять количество теплоты энергетическими единицами (1842). В системе СИ единицей работы и теплоты является джоуль.

Механический эквивалент теплоты вывел Р. Майер из данных об удельной теплоемкости газов при постоянных давлении 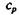и объеме 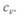Разность удельных теплоемкостей он приравнял работе, совершаемой при расширении газа, находящегося при постоянном давлении. И уравнение 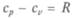названо уравне-

нием Майера [R — универсальная газовая постоянная, равная 2 кал/(моль • К)].

В работе Майера (1841) содержалась мысль о том, что «движение, теплота и, как мы намерены показать в дальнейшем, электричество представляют собой явления, которые могут быть сведены к одной силе, которые измеряются друг другом и переходят в друг друга по определенным законам». В книге «Органическое движение в связи с обменом веществ» (1845) он последовательно и систематично изложил учение о сохранении и превращении энергии (по его терминологии, силы). Воспользовавшись данными по удельной теплоемкости, Майер получил значение механического эквивалента теплоты I = 425 кГм/ккал.

Джоуль экспериментировал с проводниками электрического тока и измерял количество выделенной теплоты. Он открыл закон, по которому количество теплоты, выделенной током, пропорционально квадрату силы тока и сопротивлению. Этот же закон, независимо от Джоуля, получил в 1844 г. петербургский академик Э.Х.Ленц, поэтому он известен как закон Джоуля—Ленца. Джоуль провел много экспериментальных ра-

бот по исследованию тепловых явлений в гальванических цепях и выделению теплоты в химических реакциях.

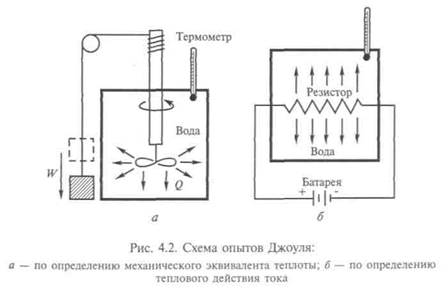
Для определения механического эквивалента теплоты Джоуль построил установку (рис. 4.2, а, б). Масса т спускается с высоты h, ее потенциальная энергия гравитации mgh теряется при опускании груза и превращается в кинетическую энергию вращающихся лопаток, которые отдают свою энергию воде, налитой в калориметр. При этом поглощенная водой энергия (в калориях) пропорциональна произведению массы воды 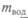на наблюдае-

мое изменение ее температуры 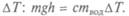Если слева в

формуле все величины выражены в системе СИ, то энергию получим в джоулях (Дж). Если массу воды взять в граммах, температуру в градусах Цельсия, то получим тепловую энергию в калориях, так как теплоемкость воды в этих единицах измерения 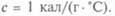Так Джоуль пришел к соотношению, которое принято сейчас: 1 кал = 4,185 Дж.

Как видно из работ Джоуля (1872), в середине 40-х годов он уже владел идеей сохранения и превращения энергии. Термин «энергия», впервые введенный в науку Юнгом, автором принципа интерференции световых волн, окончательно вошел в научный обиход в 1849 г. после работ Кельвина. Говоря о природе теплоты, Джоуль считал ее родом колебательных движений частичек тела (вслед за М. В.Ломоносовым). Независимо от Майера, он рассматривал животную силу как результат химических процессов.

Важность эквивалентности энергии (работы) и теплоты сумел оценить в 1847 г. Г. Гельмгольц.

4.2. Понятие «внутренняя энергия». Первое начало термодинамики

Закон сохранения и превращения энергии — один из основных законов, справедливых для неживой и живой природы. Важнейшее в нем — положение об эквивалентности теплоты и работы как разных форм энергии. Система изолированная не может обмениваться с окружающей средой ни веществом, ни энергией. Она большую часть времени находится в статическом состоянии, но эти условия почти не осуществимы. Если происходит обмен только энергией, систему называют замкнутой, а если энергией и веществом, — открытой. Существуют системы, помещенные в так называемую адиабатическую оболочку — это замкнутые системы, почти не обменивающиеся теплотой (например, закрытая крышкой кастрюля, термос). При равновесии ни одно из свойств системы не меняется со временем.

Функции состояния — величины, однозначно определяемые при равновесии. Нахождение этих функций и вычисление их изменений при переходе из одного состояния в другое входит в задачу термодинамики. Но абсолютные их значения не важны, и время как параметр в термодинамике не фигурирует. Фактически классическая равновесная термодинамика — это термостатика. Кроме того, в ней рассматриваются процессы, происходящие через последовательность равновесных состояний, т. е. обратимые. Да и равновесие в статическом состоянии соответствует смерти системы. Но она дает важные результаты, потому введем ее основные понятия и будем в дальнейшем путем формальных преобразований учитывать динамическую природу объектов и систем.

Полная энергия тела складывается из кинетической энергии движения тела как целого, из потенциальной энергии его во внешнем поле сил и внутренней энергии.

Внутренняя энергия — это обычно кинетическая энергия хаотического (теплового) движения его частиц и их взаимная потенциальная энергия. В последнюю включают и энергию колебательного движения атомов в молекулах, и внутриатомную энергию. В идеальном газе внутренняя энергия — энергия хаотического движения молекул. Понятие внутренней энергии относится к равновесным состояниям систем. Так как начальные и конечные состояния равновесны, на процессы, происходящие между ними, такого ограничения можно не накладывать.

Внутренней энергией системы U называют такую функцию состояния, приращение которой во всяком процессе, совершаемом системой в адиабатической оболочке, равно работе внешних сил над системой при переходе из начального состояния в конечное.

Под адиабатической оболочкой состояния меняются только путем изменения внешних параметров. И работа над системой в такой оболочке зависит не от способов перехода в состояние, а только от начального и конечного состояний. Для такой системы, перешедшей из состояния 1 в состояние 2, можно записать: 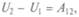причем работа внешних сил не зависит от вида пути. Внутренняя энергия U может быть положительной и отрицательной, как и работа внешних сил, и записанные соотношения нужно понимать алгебраически. Для квазистатических процессов 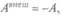т.е. можно записать 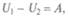работа системы при адиабатических процессах совершается за счет убыли внутренней энергии.

Итак, внутренняя энергия есть функция параметров, определяющих состояние, т. е. 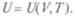Это уравнение называют калорическим уравнением состояния (в отличие от термического уравнения состояния типа 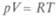для идеальных газов). Эти уравнения следуют из обобщения опыта.

Механическую теорию теплоты разрабатывал немецкий физик Р. Эмануэль, взявший себе имя Клаузиус (под которым и вошел в историю науки). Отметив, что между затраченной работой и полученной теплотой наблюдается постоянство соотношения только при процессах циклических (когда тело всегда возвращается в исходное состояние), Клаузиус ввел для уравнивания счета понятие внутренней энергии. И теплота, подводимая к воде, частично преобразуется во внутреннюю энергию расширения пара и воды, а частично — во внутреннюю энергию, которую пар возвращает при конденсации. Джоуль установил, что при рассеянии одинаковых количеств обеих энергий образуется одно и то же количество теплоты. Вслед за Джоулем, Томсоном и Гельмгольцем Клаузиус применил закон сохранения и превращения энергии к электрическим явлениям (1852): «Подобно тому как посредством теплоты может быть произведена механическая работа, так и электрический ток способен вызывать частично механическое действие, включая теплоту». У.Томсон применил этот закон к световым явлениям, химическим процессам и жизнедеятельности живых организмов, а затем — к электрическим и магнитным явлениям, установив выражение для энергии магнитного поля в виде интеграла, взятого по объему.

Молярная теплоемкость вещества определяется отношением количества теплоты, полученного одним молем вещества, к происходящему при этом увеличению температуры: 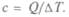Эта теплота расходуется на увеличение внутренней энергии вещества и совершение работы: 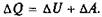Полная внутренняя энергия определяется кинетической энергией поступательного движения частиц: 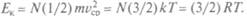Здесь R = = 8,31 Дж/(моль К), N — число молей.

Поэтому при изменении температуры меняется и внутренняя энергия.

Работа может быть совершена за счет расширения газа: 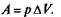Если газ находится в постоянном объеме, А = О и молярная теплоемкость определяется только изменением внутренней энергии и обозначается 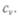Итак, 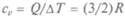= 12,6 ДжДмоль К).

Если при подводе теплоты газ имел возможность расширяться, можно вычислить работу при постоянном давлении. Из уравнения газового состояния 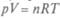видно, что увеличение температуры при постоянном давлении ведет к увеличению объема, т.е.

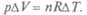
Совершаемая работа равна 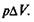Из первого начала термодина-

мики можно записать:

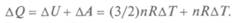
Для одного моля газа это означает, что Для молярной теплоемкости при постоянном давлении получаем значение:

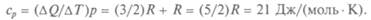
В рассматриваемой нами простой модели для газов все значения молярной теплоемкости должны быть равными, но теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме на 8,4 ДжДмоль • К). Сравните с уравнением Майе-ра: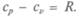

Если два атома как-то связаны, то они могут не только начать двигаться поступательно, но и вращаться вокруг общего центра масс. Поскольку каждый вид движения оттягивает на себя поступающую энергию, то изменение внутренней энергии за счет поступающей теплоты должно состоять из изменения энергии поступательного движения 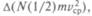вращения 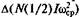и колебаний 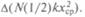При

поступательном движении двухатомной молекулы как целого возможно движение по трем равноправным направлениям, поэтому естественно предположить, что энергия делится поровну между этими тремя направлениями. При вращении молекулы, имеющей форму гантели, два направления являются равноценными — это направления, перпендикулярные оси вытянутости молекулы, на каждое из которых должна приходиться одинаковая энергия. При колебаниях (атомы связаны между собой чем-то вроде пружины) меняются потенциальная и кинетическая энергии, и на каждый тип колебания тоже приходится одинаковая энергия.

Молярная теплоемкость металлов имеет одинаковое значение, равное 25,2 ДжДмоль К) (закон Дюлонга и Пти). Это объясняется тремя степенями свободы колебаний каждого атома около своего положения равновесия в кристаллической решетке, причем на каждую приходится вдвое больше энергии, чем на поступательные (одна — на кинетическую энергию и одна — на потенци-

альную). Зависимость теплоемкости от температуры, несколько отличающуюся для разных металлов, не способна объяснить классическая теория. Кроме того, исходя из значения молярной теплоемкости, непонятно, почему электронный газ, переносящий энергию в металле, не получает тепловой энергии. Или он переносит энергию, обеспечивая теплопроводность и электропроводность, но сам энергии не поглощает?! Загадкой оказывается и огромная теплоемкость воды, в три раза большая теплоемкости металлов. Все эти нерешаемые в классической теории вопросы говорят о более сложной структуре веществ, чем эта примитивная модель.

Закон сохранения и превращения энергии в середине XIX в. приобрел права всеобщего закона природы, объединяющего живую и неживую природу. Его кратко формулируют так: «Энергия сохраняется», или: «Тепло, полученное системой, идет на приращение ее внутренней энергии и на производство внешней работы». Сохраняется именно энергия, а не теплота. Понятие энергии позволило рассматривать все явления природы и процессы с единой точки зрения, объединить все явления. Впервые в науке абстрактное понятие заняло центральное место, оно пришло вместо ньютоновой силы, соответствующей чему-то осязаемому, наглядному, конкретному, хотя и облаченному Ньютоном в математические одежды.

Понятие «энергия» прочно вошло в нашу жизнь. Под энергией чаще всего понимают способность тела совершать работу. Лорд Кельвин признал, что силы могут исчезать и возникать, а энергия не уничтожается. Это понятие соответствовало и его религиозным взглядам: он считал, что Творец в самый момент творения мира наделил его запасом энергии, и этот божественный дар будет существовать вечно, тогда как эфемерные силы подвержены многим превратностям, и с их помощью в мире ткется ткань явлений преходящих.

Первое начало термодинамики, связанное с законом сохранения и превращения энергии, акцентирует внимание на внутренней энергии: приращение внутренней энергии при переходе системы из одного состояния в другое складывается из суммы работы внешних сил над системой и количества теплоты, получаемого системой. Оно требует сохранения энергии изолированной системы, но не указывает направления, в котором процессы могут происходить в природе. Это направление указывается вторым началом. Кроме того, второе начало вводит температурную шкалу, не связанную с рабочим веществом термометра и его устройством. Два начала позволяют установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состояниях термодинамического равновесия или около него.

4.3. Преобразование тепловой энергии в механическую работу

Исследовать работоспособность тепловых машин решил молодой французский инженер Н.С.Карно. Его работа «Размышление о движущей силе огня и о машинах, способных развивать эту силу» (1824), в которой он сформулировал общий и абстрактный методы решения специальной задачи, вышла за пределы специального исследования, положив начало новой науке — термодинамике.

Анализируя механизм действия тепловых машин, Карно исходил из того, что для их работы нужно наличие разности температур 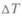и затем их выравнивание, так же, как для работы водяных машин необходима разность уровней воды. Поэтому «возникновение движущей силы обязано в паровых машинах не действительной трате теплорода, а переходу его от горячего тела к холодному, т.е. восстановлению его равновесия». Но определяет ли 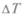производимую машиной работу? Ведь возможен процесс выравнивания температур без всякой работы, как при непосредственном тепловом контакте. Для того чтобы работа производилась, нужен посредник, рабочее вещество, которое было бы способно отобрать теплоту у нагревателя (более горячего тела) при более высокой температуре и отдать ее холодильнику (более холодному телу) — при более низкой.

Карно рассмотрел идеальную машину, которая имела бы большую эффективность, чем любая реальная машина. Идеальна она потому, что в ней отсутствует внутреннее трение, а процесс характеризуется только двумя температурами.

Теорема Карно, доказанная в этой работе: эффективность любой тепловой машины, работающей при температурах 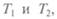причем 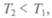меньше эффективности идеальной машины. Кар-

но не вычислял коэффициент полезного действия (КПД), но указал, что он пропорционален разности падения температур единицы теплорода: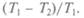

Идеи Карно в течение 10 лет не вызывали интереса, пока Клапейрон не выпустил свою книгу (1834), в которой он дал анализ работы Карно, перевел ее на математический язык и несколько улучшил сам цикл Карно — заменил его другим, теперь общеизвестным циклом из двух адиабат и двух изотерм, называемый циклом Карно. Клапейрон впервые употребил графическое изображение обратимых круговых процессов и вычислил работу как соответствующую площадь на графике.

Превращение теплоты в работу для практических целей важно, как и превращение одного вида энергии в другой. Обратимся к схеме работы тепловой машины. В цилиндре машины помещается при атмосферном давлении вещество (газ), называемое рабочим телом. Повысим его температуру, не меняя давление, и газ должен расшириться. Поршень пере-

местится на расстояние х, причем он будет двигаться против внешнего давления атмосферы. Если площадь поршня равна s, то совершается работа против силы, равной ps, так как р — сила, приходящаяся на единицу площади. Поршень переместился на расстояние х, и работа на этом пути 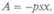Здесь поставлен знак минус, так как работа совершается

газом, который отдает ее внешней среде, перемещаясь в направлении, противоположном приложенной силе. Поскольку произведение sx есть изменение объема газа 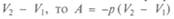и равна теплоте,

затраченной на нагревание газа.

Пусть газ под поршнем в цилиндре находится в равновесии с окружающей средой. Будем медленно выдвигать поршень из цилиндра, не нарушая равновесия в каждый данный момент и сохраняя постоянство температуры. Этот процесс соответствует эмпирическому закону Бой-ля — Мариотта: pV= const. Точка 7, представляющая состояние газа, перейдет на плоскости р, V — в точку 2. Если опять же медленно и при постоянной температуре сжимать газ, то точка 2 вернется в точку 1, потому что изотермический процесс обратим. Существует и другой обратимый процесс в идеально теплоизолированном сосуде — адиабатический. Этот процесс тоже очень медленный, так что температура во время сжатия или расширения выравнивается во всех точках, но меняется в зависимости от объема: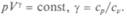

Оба этих обратимых процесса, конечно, идеализированы, реальные процессы могут только приближаться к ним, поскольку всегда есть какие-то потери теплоты на теплоизоляцию, вязкость среды и т. п. Цикл Карно состоит из двух изотермических и двух адиабатических процессов, которые образуют на графике в координатах (р, V) криволинейный четырехугольник. Адиабаты идут круче изотерм, поэтому они образуют боковые линии, а изотермы — основания. Теплота подводится и отнимается при изотермическом процессе, поэтому верхняя изотерма отвечает расширению газа в тепловом контакте с нагревателем температуры Т₁, а нижняя — сжатию при контакте с холодильником при температуре Т₂. Пусть газ получает от нагревателя теплоту Q₁,а холодильнику отдает теплоту Q₂. Тогда за весь цикл он получит теплоту Q = Q₁ - Q₂, равную совершенной работе А. Отношение работы А к теплоте, полученной у нагревателя (с нагревателем связаны основные затраты, ведь это ему нужно топливо), называется коэффициентом полезного действия теплового двигателя: КПД =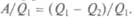

Коэффициент полезного действия двигателя, таким образом, определяется разностью температур нагревателя и холодильника, деленной на температуру нагревателя: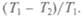

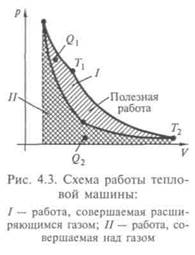
На рис. 4.3 графически представлена совершенная работа при Q = А + Q₁, Возможность построения машины без холодильника, т.е. с КПД = 1, которая могла бы превращать в работу всю теплоту, заимствованную у теплового резервуара, не противоречит закону сохранения энергии. По своему практическому значению она

не уступала бы перпетуум-мобиле, так как могла бы производить работу за счет почти неисчерпаемых запасов внутренней энергии, содержащихся в воде морей и океанов, в атмосфере и недрах Земли. Такую машину У.Оствальд назвал перпетуум-мобиле второго рода (в отличие от перпетуум-мобиле первого рода — вечного двигателя, производящего работу из ничего). Карно исходил из идеи невозможности вечного двигателя, опираясь на факты многочисленных опытов, которая была возведена в постулат, названный вторым началом термодинамики.

На основе термодинамики У. Томсон (впоследствии лорд Кельвин) предложил абсолютную шкалу температур (см. рис. 4.1). Он исходил из того, что КПД всех обратимых двигателей определяется только абсолютными температурами холодильника и нагревателя. Машина Карно может использоваться для градуировки шкалы, если закрепить точку таяния льда. Проведя цикл Карно между данным телом и тающим льдом и измерив соответствующие количества теплоты, можно из прямой пропорциональности количества теплоты и температур найти абсолютную температуру (в К). С 1954 г., по определению X Генеральной конференции по мерам и весам, температура тройной точки воды (точка равновесного сосуществования льда, воды и пара) считается равной 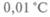(273,16 К) при давлении 6,09 гПа.

Можно ли повысить КПД за счет уменьшения температуры холодильника? Казалось бы КПД = 1 при Т₂ = 0, но все газы гораздо раньше начинают сжижаться, т. е. перестают быть газами, следовательно, абсолютный нуль температур недостижим. Это и составляет содержание третьего начала термодинамики, утверждающего, что нельзя охладить вещества до температуры абсолютного нуля посредством конечного числа шагов. Понимание этого начала требует представлений об атомном строении вещества, тогда как другие начала есть обобщение непосредственного опыта и не зависят ни от каких предположений. Но: можно ли повысить КПД за счет увеличения температуры нагревателя? По этому пути развивается вся теплотехника (плазменные двигатели, например, имеют температуру горячего вещества до 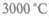), но этим путем

повышение КПД происходит медленней, чем понижением Т₂. А когда хотят понизить температуру холодильника, обычно забывают, что на это надо затратить работу хотя бы с помощью жид-

кого воздуха. В холодильных установках теплота отбирается от холодного тела и отдается горячему, но только за счет работы извне. Смысл второго начала термодинамики в том и состоит, что нельзя непрерывно получать работу, не имея резервуара энергии. Для Земли таким источником энергии является Солнце. На солнечной энергии работают и гидростанции, и солнечные батареи, и ветряные двигатели. Их работа не противоречит второму началу термодинамики. В 1851 г. Кельвин сформулировал второе начало иначе: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара». Близкую формулировку дал Макс Планк: «Невозможно построить периодически действующую машину, единственным результатом которой было бы поднятие груза за счет охлаждения теплового резервуара». Поэтому иногда говорят: «Процесс Томсона — Планка невозможен». Клаузиус выдвинул второй постулат в таком виде: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Можно показать, что все эти варианты второго начала эквивалентны и вытекают один из другого.

4.4. Понятие «энтропия». Суть спора о «тепловой смерти Вселенной»

Феноменологическая термодинамика свела всю совокупность тепловых явлений в три начала без всякой модели вещества, т. е. они просто описывают все явления (отсюда и термин — феноменологическая). Клаузиус не только уточнил идеи Карно, но отказался от теплорода, объясняя природу теплоты в соответствии с концепцией атомизма. Важную роль в этом сыграла и новая абстрактная величина — энтропия (от греч. entropia — поворот, превращение), введенная им в 1865 г. Клаузиус определил понятие энтропии и показал, что в термически изолированных системах энтропия при обратимых процессах не изменяется, а при реальных и необратимых — растет всегда. Поэтому она является как бы мерой отклонения реальных процессов от идеальных.

Энтропия, как характеристика состояния системы сыграла в развитии науки фундаментальную роль. Как каждому уровню высоты над поверхностью Земли отвечает своя потенциальная энергия, так и каждому состоянию — своя энтропия. Как работа в поле тяжести не зависит от вида пути, а определяется только изменением потенциальной энергии, так и энтропия не зависит от вида процесса, определяясь только состоянием. Понятие энтропии как функции состояния было введено из рассмотрения квазистатических циклов.

Обратимся к бесконечно малому циклу Карно. Если обозначить через S сумму величин (Q/T), то для любого обратимого процесса =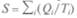

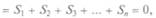тогда как сумма количеств теплоты Q не равна нулю. В результате завершения квазистатического цикла в источниках работы и теплоты происходят изменения. Между ними должны быть общие связи, выражением которых служит, с одной стороны, принцип эквивалентности теплоты и работы, с другой — теорема о сумме приведенных теплот.

Согласно второму началу термодинамики, из всех тепловых двигателей, работающих при данных температурах нагревателя и холодильника, обратимый двигатель имеет наибольший КПД, т. е. КПД необратимого двигателя меньше, чем КПД обратимого. Как меняется энтропия в необратимых процессах? Нагреватель отдает и получает теплоту Q₁при одной и той же температуре, т.е. его энтропия не меняется: 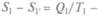^_ Q₁/T₁ = 0. В то же время энтропия холодильника или окружающей среды растет: 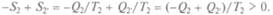При спаренной работе холодильник получает теплоту Q₁ от необратимого двигателя и отдает теплоту Q₂ обратимому. Температура окружающей среды из-за ее очень большого объема практически не меняется от передачи теплоты Q₂, но это изотермический процесс, а он обратим, т. е. для окружающей среды: 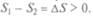Таким образом, получилась замкнутая система — источник внешней работы, нагреватель, холодильник и спаренные двигатели. В ней есть только одно необратимое звено, и оказалось, что энтропия системы выросла.

Можно считать, что рост энтропии в изолированной системе есть мера необратимости какого-то процесса в ней. Всякий необратимый процесс в замкнутой системе ведет к росту энтропии. Рассуждая в обратную сторону, придем к формулировке невозможности построить вечный двигатель второго рода. Существование энтропии доказано для обратимых процессов и выражает второе начало термодинамики в наиболее общей форме. С этим законом известный физик и астроном А. Эддингтон связал стрелу времени. Точнее, все необратимые процессы могут идти только в направлении вперед во времени, тогда как обратимые — в обе стороны. Но почти все процессы являются необратимыми.

Второе начало термодинамики претерпело эволюцию — от тепловой аксиомы, выражающей опытный факт о невозможности самопроизвольного перехода теплоты от холодного тела к горячему (1850), к принципу эквивалентности превращений (1854) и к принципу существования и возрастания энтропии (1865). Итак, в изолированной системе энтропия может только возрастать, что эквивалентно второму началу термодинамики.

Основоположники классической термодинамики — Кельвин и Клау-зиус — считали, что ее начала годятся для любой изолированной системы, в том числе и для всей Вселенной. Отсюда — вывод о неизбежности ее «тепловой смерти», т.е. такого состояния, когда все процессы прекратятся, и мир перейдет в состояние термодинамического равновесия. Они не находили процессов, в которых энергия могла бы повышать свое качество, считали, что все тепловые явления самопроизвольно происходят

только в одном направлении: горячие тела охлаждаются, холодные — сами по себе не нагреваются, т. е. распределение энергии необратимо. Но они отделяли это свойство мира от сохранения количества энергии при всех превращениях. Второе начало термодинамики указывает естественное направление изменения распределения энергии, не зависящее от количества энергии. Идеи Клаузиуса и Кельвина носили описательный характер, но вызвали дискуссии.

Так, Ранкин выдвинул гипотезу реконцентрации энергии: Вселенная окружена особой эфирной оболочкой, обладающей свойствами зеркальной поверхности, и энергия может не рассеиваться, а концентрироваться в каких-то центрах мира, где температура будет повышаться. Возникшая разность температур вновь нарушит тепловое равновесие. В ответ Клаузиус показал, что никакое вогнутое зеркало не может дать температуру выше той, которая была присуща телу. Папа Пий XII считал: «Закон энтропии, открытый Рудольфом Клаузиусом, дал нам уверенность в том, что в изолированной материальной системе в конце концов процессы в макроскопическом масштабе когда-то прекратятся. Эта печальная необходимость свидетельствует о существовании Необходимого Существа». Энгельс расценил эти выводы как доказательство необходимости сотворения мира, как противоречие закону сохранения энергии, если второе начало говорит о качественном уничтожении энергии. Он указывал, что «вопрос будет решен окончательно лишь в том случае, если будет показано, каким образом излученная в мировое пространство теплота может быть снова используемой». Его «Диалектика природы» построена на идее круговорота энергии.

Начала термодинамики свидетельствуют о том, что энергия превращается из одной формы в другую так, чтобы энтропия возрастала (энергию и энтропию и называли «царица мира и ее тень»). Все виды энергии классифицируют в порядке возрастания «ценности». Высший класс у тех, которые способны превращаться в большее число форм энергии, им присущи минимальные хаос и энтропия. Средний класс — у химической энергии, а низший — остается теплоте, энергетические превращения которой ограничены принципом Карно. Самопроизвольные превращения энергии с ее деградацией и ростом энтропии — это преобразования от высших форм к низшим. Направление потока превращения энергии во Вселенной задается главным образом гравитацией, преобладающей в космосе количественно и имеющей почти нулевую энтропию. Поэтому КПД гидроэлектростанций больше, чем тепловых.

Но почему же гравитационная энергия до сих пор не превратилась в свет и теплоту? Больцман считал гипотезу «тепловой смерти Вселенной» Клаузиуса — Томсона плодом недоразумения. Он признал вероятностный смысл второго начала термодинамики и распространил его на Вселенную: «Если смотреть на мир как на нечто бесконечное, то возникают опять те же самые противоречия, какие получались, когда бесконечное считалось только пределом». Больцман нарисовал картину огромного

космического пространства, возможно, даже бесконечного во времени и пространстве, полная энтропия которого достигла своего максимального значения, но в котором имеются области, где в данный момент энтропия уменьшается. «Данный момент» может длиться биллион лет, а «данная область» может насчитывать биллионы галактик. Возможно, что та ничтожно малая область из этого бесконечного пространства, где находимся мы, и есть одна из областей гигантской флуктуации. В некоторый момент в прошлом энтропия уменьшилась, а сейчас возрастает. В вечном и бесконечном потоке материи в некотором месте появилась зона упорядоченности, а ныне порядок постепенно разрушается. Где-то процессы могут идти в обратном порядке, тогда и время там должно идти в обратном направлении, поскольку рост энтропии связан со стрелой времени. Но в этом случае и наше понимание причинности должно измениться на обратное: выходит, в тех областях пространства и времени следствие предшествует причине?! Больцмана это не смущало, он находил, что живое существо всегда будет определять путь от прошлого к будущему как от события маловероятного к более вероятному, и не отличит нарушений, как мы не отличаем верха и низа в пространстве. Эта идея Больцмана получила название флуктуационной гипотезы: на фоне всеобщей тепловой смерти возникают и эволюционируют отдельные миры, переходя из маловероятных состояний в более вероятные, что обуславливает протекание необратимых процессов.

Наблюдения в области эволюции звездных ассоциаций показывают, что процесс образования звезд не сводится к спонтанным флукту-ациям, что одни формы энергии непрерывно превращаются в другие. Хотя огромное число достаточно изолированных галактик охвачено наблюдениями, пока не видели галактики в состоянии тепловой смерти. Таким образом необходимо расширить рамки флуктуации, где находимся мы, до размеров всей наблюдаемой Вселенной. По этому поводу Ландау и Лифшиц высказали замечание, что «неизмеримо большей вероятностью обладала бы флуктуация в размере одной только Солнечной системы, что было бы достаточно для обеспечения существования наблюдателя». Но Больцман пытался объяснить существование необратимых процессов во Вселенной на основе обратимых элементарных законов природы. Русский физик, астроном и метеоролог А.А.Фридман в 1922 г. утверждал, что, если уравнения теории тяготения Эйнштейна применимы ко Вселенной, то она должна меняться со временем — либо расширяться, либо сжиматься, либо пульсировать. Хотя модели расширяющейся Вселенной называют моделями Фридмана, но он не обсуждал начальный момент, считая, что для этого недостаточно данных. В 30-е гг. английские астрофизики А. Милн и М. Мак-Кри показали, что и в теории Ньютона можно получить режим сжатия и разрежения мира (см. гл. 9).

Флуктуационную гипотезу уточняли введением поправок на скорости и массы тел. Я.П.Терлецкий считал, что для больших масс вещества возможны большие флуктуации сжатия и разрежения. В периоды сжатия идут процессы конденсации, возникают звезды и планеты, в периоды разрежения, когда звезды «разбегутся» на достаточно большие расстояния, неизбежен распад конденсированных систем и превращение их в однородную газовую среду. Оценки, приведенные П.Дираком, Дж.Уи-

лером, Р. Фейнманом и Р. Пенроузом с учетом собственных гравитационных полей космических тел по строгим формулам ОТО показали, что в момент, когда сжатие прекращается и начинается разрежение, общекосмическое время поворачивает вспять, и на мгновение могут потухнуть все звезды. Такой вывод должен был служить доказательством теории «пульсирующей Вселенной», одна из теорем которой утверждает, что в этот момент меняется и знак материи. В 60-е гг. А. Д. Сахаров выдвинул гипотезу, по которой до момента рождения Вселенной существовала анти-Вселенная, где все было зеркальным отражением нашего мира, она постепенно сжалась в массу сверхплотного вещества, ставшего нейтральным. Из нее при сверхвысоких температуре и плотности возникла Вселенная, так как в тот момент образовалось больше протонов и нейтронов, чем антипротонов и антинейтронов, поэтому нам неизвестны антимиры и антигалактики.

В 1922 г. немецкий физико-химик В. Нернст, считая тепловую смерть Вселенной невероятной, обратился к явлению радиоактивности, которое «познакомило нас с энергией такого могущества, о котором мы ранее не имели представления». Образование тяжелых атомов, скопление их в холодные звезды, разогреваемые за счет высокой радиоактивности, превратит их в раскаленные. Во Вселенной возникнут центры концентрации энергии, противодействующие тепловому равновесию. Р. Милликен основывал подобные выводы на свойствах космических лучей, пополняющих радиацию, непрерывно испускаемую звездами. Позже были открыты объекты, обладающие достаточной мощностью, чтобы быть источником космических лучей: сверхновые (взрывающиеся) звезды, радиогалактики (гигантские облака истекающих из них электронов, невероятно богатых энергией), галактики Сейферта (галактики с очень ярким и турбулентным ядром, описанные в 1943 г. американским астрономом К.Сейфертом), источники рентгеновского излучения, пульсары и квазары, выделяющие огромные количества энергии. В ядрах галактик и квазарах столь необычные условия, что на них невозможно распространять сложившиеся представления, т.е. необходимы новые модели (см. гл. 9).

Идеи непрерывного творения материи возникали неоднократно. Так, в 1948 г. ученые Кембриджского университета Г. Бонди, Т. Годд и Ф.Хойл выдвинули гипотезу стационарной Вселенной. Они оценили число порожденных за 100 лет из «ничего» атомов водорода для восполнения убыли материи из-за разбегания — 1 атом в кубе с ребром 100 м (!), т.е. за 5 млрд лет должно было образоваться всего 4 кг атомов. Но открытие в 1965 г. однородно распределенного в пространстве излучения с Т = 2,7 К, истолкованного как «реликтовое» (оставшееся от Большого Взрыва), ослабило интерес к этой теории. Пока не ясно, существует ли скрытая полевая форма материи, непрерывно порождающая известные нам формы.

Термодинамика Вселенной — это теории звездных атмосфер и внутреннего строения звезд. Излучение, рождающееся в недрах звезды, покидает ее фотосферу, достаточно тонкую ее область. В ней происходит лучистый перенос энергии, который изучается в теории и сравнивается с данными наблюдений по распределению энергии в непрерывном спектре Солнца и звезд. Считают, что атмосферы спокойных звезд находятся в состоянии лучистого

равновесия, т. е. каждый элемент объема излучает столько энергии, сколько поглощает. Равновесное излучение в полости определяется только абсолютной температурой, его интенсивность не зависит ни от свойств полости, ни от места, ни от направления. Для него выведены законы Вина, Кирхгофа, Стефана — Больцма-на. В звездных атмосферах ситуация несколько сложнее, но можно допустить локальность равновесного излучения.

Релятивистская термодинамика лежит в основе современной космологии. На обобщенных термодинамических принципах построены теория процессов в таких экзотических объектах, как «черные дыры», и модель эволюции Вселенной, в которую необходимо включить и открытое Хабблом красное смещение в спектрах галактик как одно из доказательств расширения Вселенной.