Статистические методы исследований

Применение методов статистического анализа.Методы количественной оценки результатов исследований лесных компонентов разработаны математиками, ботаниками и лесоводами с учетом положений теории вероятности и её практического приложения – вариационной статистики. В настоящем учебном пособии изложены некоторые положения, необходимые как для понимания сути подходов к изучению случайных явлений (величин), преобладающих в лесных сообществах, так и для применения их в исследовательской работе.

Все явления в природе делятся на закономерные и случайные. Закономерные явления вызываются действием одного фактора, в то время как случайные явления вызываются одновременным действием и взаимодействием двух или большего числа факторов (причин). Примером закономерного явления может служить равномерное движение (человека, автомобиля, самолета), когда результат определяется действием одного фактора – времени движения.

S = V ∙ t, (5)

где: S – пройденный путь,

V – скорость движения,

t – время движения.

В наиболее общем виде эта формула имеет вид:

Y = a ∙ x , (6)

где: Y – зависимая переменная,

a – постоянная величина,

x – независимая переменная.

Пример случайной величины: объем ствола зависит от высоты ствола, его диаметра и показателей формы ствола (видового числа, коэффициентов формы). Каждый из этих показателей (факторов) влияет на конечный результат – величину объема ствола. Указанные факторы действуют не только каждый в отдельности, но они связаны друг с другом – изменение одного их них ведет к изменению других и их взаимодействие также оказывает влияние на конечный результат.

Величины, вызываемые одновременным действием и взаимодействием двух или большего числа факторов, называют случайными или вероятностно-стохастическими. Такие величины могут быть вычислены лишь с определенной долей вероятности даже в случае точного измерения действия каждого известного фактора (показателя) – высоты, диаметра и коэффициентов формы ствола, так как остаются неизвестными характер и степень влияния их взаимодействия, а так же влияния неучтенных факторов.

Использование вариационной статистики в лесоводственных и лесобиологических исследованиях позволяет решить ряд задач:

- дать оценку среднего значения (например, среднего диаметра ствола в древостое), амплитуды и особенностей изменчивости этого показателя;

- установить точность исследований и достоверность полученных результатов – статистических показателей, характеризующих степень соответствия объектов при их выборочном изучении (выборочной совокупности) соответствующим параметрам генеральной совокупности;

- сравнить данные исследований, полученные в различных лесорастительных условиях;

- сравнить между собой особенности изменчивости различных показателей (величин, характеристик) изучаемого объекта;

- сравнить данные, полученные разными исследователями;

- установить характер взаимосвязи различных показателей (характеристик) объекта исследований;

- выявить особенности динамики характеристик объекта;

- прогнозировать изменения характеристик объекта за пределами изученной области, и др.

В лесоводственных исследованиях принято изучать выборочные совокупности (выборки), перенося результаты и выводы на генеральную совокупность. Генеральной совокупностьюназывается множество каких-либо однородных изучаемых элементов, из которого по определенному правилу выделяют некоторое подмножество, называемое выборкой, которая является объектом анализа. В большинстве случаев выборочная совокупность должна извлекаться из генеральной совокупности с использованием определенных способов для того, чтобы обеспечить объективность в формировании выборки.

Пример: необходимо изучить продуктивность культур сосны в типе леса С. ртр в южной тайге Среднего Урала в возрасте 30 лет с целью анализа особенностей формирования древостоев в фазе жердняка. Согласно поставленной цели и конкретных задач ее достижения следует изучить все большое количество участков таких культур в южной тайге Среднего Урала. Но изучить все участки культур крайне затруднительно; более того, делать это нецелесообразно в связи с большими затратами времени, труда и средств, не оправдывающими высокой достоверности полученных результатов. Использование выборки (выборочной совокупности) позволяет многократно сократить затраты на проведение исследования, получить при этом достаточно точные результаты и сделать достоверные научные выводы. Для повышения точности исследований и достоверности результатов рекомендуется проводить исследование в нескольких повторностях (с использованием нескольких выборок – пробных площадей), число которых рекомендуется от 2 до 6 (в среднем 4).

Статистически обоснованным должен быть и объем выборки (число наблюдений, число деревьев на пробной площади). Он определяется по формуле:

где: N – число деревьев;

t – критерий Стьюдента (при большом числе наблюдений t = 1,96);

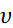– коэффициент вариации (диаметра ствола = 20 – 23%);

p – допустимая ошибка опыта (3%).

Отсюда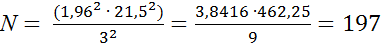

Такое количество наблюдений (число деревьев, округленно 200) должно быть принято в исследованиях на каждой пробной площади.

Для получения необходимой точности опыта (точности определения средних значений диаметра древостоя и других таксационных показателей и достоверности статистических характеристик их варьирования) число наблюдений должно быть не менее 200. При меньшем числе наблюдений (числе деревьев на пробной площади) распределение их не будет с достаточной точностью отражать особенности варьирования диаметра ствола и других таксационных показателей в генеральной совокупности.

Вариационный анализ. При исследовании выборочной совокупности определяют среднее значение изучаемого таксационного показателя, стандартно отклонение, дисперсию, коэффициенты вариации, асимметрии и эксцесса, достаточно полно отражающие особенности варьированных (изменчивости) таксационного показателя (рис. 2).

В статистике среднее арифметическое определяют как частное, полученное делением суммы всех наблюдений на число наблюдений:

где: M – среднее значение;

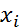– результаты конкретных измерений;

N – общее число измерений таксационного показателя (равное числу измеренных деревьев).

Среднее арифметическое (среднее значение) определяет положение ряда распределения относительно точки пересечения координат (нулевого значения изучаемого таксационного показателя).

Стандартное (среднеквадратическое) отклонение является основной статистикой, характеризующей изменчивость (варьирование) изучаемого таксационного показателя (изучаемой величины). За стандартное отклонение принята 1/6 часть амплитуды колебаний значений изучаемого таксационного показателя при распределении его по закону Лапласа-Гаусса. Стандартное отклонение равно корню квадратному из суммы квадратов отклонений значений изучаемой величины от среднего значения деленной на число степеней свободы N – 1:

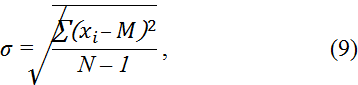
где: σ – стандартное отклонение;

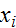– значения показателя;

М – среднее значение;

N – число наблюдений.

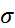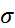В распределении по закону Лапласа-Гаусса ординаты, ограничивающие – и + , совмещаются с точками перегиба кривой распределения; прямая, соединяющая точки перегиба, параллельна оси абсцисс (рис. 2).

Стандартное отклонение измеряется в тех же единицах, в которых измеряется изучаемая величина, в связи с чем стандартное отклонение не может служить средством сравнения размаха варьирования разнородных совокупностей (например, диаметра и объема ствола, диаметра и высоты ствола). Этой цели удовлетворительно отвечает относительный параметр – коэффициент вариации– выражаемое в % частное от деления стандартного отклонения на среднее значение М изучаемой величины:

где: V – коэффициент вариации.

Коэффициент вариации представляет собой нормированное стандартное отклонение; это относительная мера рассеяния при среднем значении, принятом за единицу.

Чем выше значение коэффициента вариации, тем выше изменчивость изучаемого таксационного показателя, выше амплитуда его индивидуальной изменчивости, следовательно, имеется возможность отбора выдающихся особей (деревьев), что имеет значение в лесной селекции. Наоборот, при низкой индивидуальной изменчивости возможность отбора высокопродуктивных особей снижается, селекционное ее значение уменьшается. При увеличении коэффициента вариации до величины более 50% его реальный смысл теряется, так как такой таксационный показатель не относится к числу сформировавшихся, генетически обусловленных (например, распределение подроста под пологом материнского полога древостоя).

Дисперсия– это возведенное в квадрат стандартное отклонение, позволяющее избавиться от отрицательного знака стандартного отклонения. Дисперсия, как и стандартное отклонение и коэффициент вариации, является важнейшим параметром оценки изменчивости изучаемой величины, широко применяемым в статистическом исчислении.

Ошибка среднего значения (среднеквадратичная ошибка, стандартная ошибка, ошибка выборки) используется для вычисления показателя точности опыта (относительной ошибки), который оценивает точность определения среднего значения исследуемой величины (степень соответствия его среднему значению генеральной совокупности). Он рассматривается как процентное отношение ошибки среднего значения исследуемой величины к самой средней величине:

где: P – показатель точности опыта;

m – ошибка среднего значения.

Корреляционный анализ. Метод корреляционного анализа применяют для установления связи между случайными величинами. Установление связи между двумя случайными величинами называется парной корреляцией, а между тремя или большим числом случайных величин – множественной.

Парная корреляция может быть линейной и нелинейной, положительной и отрицательной (рис. 11 – 14). Линейная связь является прямолинейной, а нелинейная – криволинейной. При положительной корреляции увеличение значений одной случайной величины ведет к увеличению значений другой (с увеличением диаметра ствола деревьев увеличивается их высота). Отрицательная связь предполагает уменьшение одной случайной величины при увеличении другой. Примером нелинейной корреляции является связь высоты ствола с его диаметром, когда с увеличением диаметра возрастает и высота, но связь между ними является криволинейной, затухающей. Примером обратной связи является связь числа стволов на 1 га с их размерами.

Корреляция между случайными величинами не отражает причинную связь, поэтому можно рассматривать как зависимость второй случайной величины от первой, так и зависимость первой величины от второй, то есть можно составлять как первое, так и второе корреляционные уравнения. В некоторых случаях имеет логический смысл лишь одно корреляционное уравнение, в частности, уравнение зависимости таксационных показателей деревьев от их возраста. В лесоводственных исследованиях чаще всего устанавливают зависимость различных таксационных показателей деревьев от диаметра ствола на высоте груди; на основании полученных результатов исследований этих закономерностей составляют таксационные таблицы для их использования в научных и производственных целях.

Для оценки тесноты связи двух случайных величин при линейной их связи служит коэффициент корреляции, а криволинейной – корреляционное отношение. Коэффициент корреляции является частным случаем корреляционного отношения. В корреляционной связи одному значению аргумента соответствует приближенное значение функции или некоторое множество значений функции, в той или иной степени близких друг к другу. Чем теснее связь признаков, тем больше корреляционная связь приближается к функциональной.

На лесные и ботанические объекты воздействуют факторы в их широком разнообразии, поэтому между признаками этих объектов встречаются исключительно корреляционные связи. В одной и той же парной связи может существовать как прямая, так и обратная связь, например, при увеличении размеров деревьев хвойной породы с возрастом до определенного уровня число шишек на дереве увеличивается, после достижения этого уровня число шишек на дереве снижается. В задачу лесобиолога входит объяснить причины этого явления, а в задачу лесовода – использовать с максимальной лесоводственной эффективностью динамику возобновительной способности лесов.

При изучении корреляционных связей у древесных растений методом парной корреляции можно считать доказанной лишь ту связь, механизм которой понятен исследователю; в некоторых случаях при механическом подходе можно установить связь, которой на самом деле нет. Это происходит в случае, когда два изучаемых

yy

xx

Рис. 11. Положительная линейная Рис. 12. Положительная

связь нелинейная связь

yy

xx

Рис. 13. Отрицательная линейная Рис. 14. Отрицательная

связь нелинейная связь

признака в сильной степени зависят от какого-либо третьего признака или совокупности признаков. Поэтому методически более правильным будет одновременное изучение связей всего комплекса признаков с использованием множественной корреляции и корреляционных плеяд.

Чем ближе эмпирическое распределение признака к симметричному и, более того, к нормальному, тем больше вероятность существования корреляционных связей данного признака с другими признаками. Для выявления этих связей иногда требуется большое число измерений (наблюдений). При изучении связи двух взвешенных рядов распределения составляют корреляционную решетку с вычислением показателей тесноты связи и построением в последующем эмпирической линии регрессии, позволяющей определить характер зависимости одной величины от другой. При прямолинейной связи вычисляют коэффициент корреляции и коэффициент ранговой корреляции Спирмена, а при криволинейной – корреляционное отношение независимо от объема выборки.

Квадрат коэффициента корреляции (r²) и корреляционного отклонения является показателем связанности, взаимообусловленности изменчивости коррелируемых признаков; он является показателем, более точно отражающим характер их связи в сравнении с коэффициентом корреляции и корреляционным отношением.

Перспективные вопросы лесокультурных