Основные этапы структурного синтеза
Процедуру структурного синтеза ЦА можно условно разделить на 5 этапов.
1. Определение числа физических входов, физических выходов и количества элементов памяти, необходимых для синтеза.
Число необходимых для синтеза элементов памяти определяется как
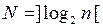 ,
,
что дает наименьшее из решений также используемого для этих целей неравенства
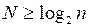 ,
,
где n – число состояний абстрактного автомата, 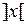 – округление до ближайшего целого в большую сторону. Аналогично может быть определено число двоичных разрядов для кодирования входных и выходных сигналов.
– округление до ближайшего целого в большую сторону. Аналогично может быть определено число двоичных разрядов для кодирования входных и выходных сигналов.
В качестве элементов памяти используются элементарные автоматы, являющиеся автоматами Мура и имеющие два устойчивых состояния. Каждому состоянию ЭА соответствует свой выходной сигнал. Число входов обычно от 1 до 3.
2. Кодирование состояний автомата.
Под кодированием состояний ЦА понимается сопоставление каждому состоянию некоторого уникального двоичного кода, разрядность которого определяется числом используемых элементов памяти.
Основные этапы структурного синтеза рассмотрим на примере.
Пусть синтезируемый автомат Мили задан совмещенной таблицей переходов-выходов (табл. 5.29).
Таблица 5.29
| x \ a | ||||
| x1 | 3/2 | 3/1 | 2/3 | 1/2 |
| x2 | 2/3 | 2/2 | 4/1 | 1/3 |
Для кодирования четырех состояний автомата понадобятся два двоичных разряда. Закодируем состояния автомата произвольными двухразрядными двоичными комбинациями Q1Q2 (табл. 5.30).
Кроме того, для удобства закодируем входные и выходные сигналы (табл. 5.31, 5.32). Для кодирования трех выходных сигналов понадобятся три двухразрядные двоичные комбинации Z1Z2. Для кодирования двух входных сигналов достаточно одного двоичного разряда S.
Таблица 5.30 Таблица 5.31 Таблица 5.32
| Q \ a | Z \ y | S \ x | x1 | x2 | |||||||||
| Q1 | Z1 | S | |||||||||||
| Q2 | Z2 |
При кодировании входных и выходных сигналов автомата следует учитывать, что для синтеза схемы такого автомата может потребоваться реализация подсхем кодирования входных и декодирования выходных сигналов. Таким образом, общая цена схемы может увеличиться по отношению к цене схемы, синтезированной с использованием некодированных входных и выходных сигналов автомата.
В качестве ЭА, используемых для реализации памяти автомата, рассмотрим Т-триггеры (см. табл. 5.24).
3. Составление кодированной таблицы переходов и выходов синтезируемого автомата(табл. 5.33).
В каждую строку кодированной таблицы переходов и выходов записывают переход автомата из состояния ai в состояние aj под воздействием некоторого входного сигнала и формируемый при этом выходной сигнал. Состояния автомата записываются в таблицу в закодированном виде. Для автомата Мура выходные сигналы можно не указывать, так как они определяются только состояниями автомата и не зависят от входных сигналов.
В нижней строке табл. 5.33 указаны моменты формирования автоматом соответствующих сигналов.
Таблица 5.33
| S | Q1 | Q2 | Q1 | Q2 | q1 | q2 | Z1 | Z2 |
| t | t | t+1 | t | t |
В первом столбце табл. 5.33 записаны кодированные значения входных сигналов, формирующие переходы автомата.
В столбцах 2 и 3 записаны двоичные комбинации Q1Q2, кодирующие исходное состояние автомата в момент времени t, а в столбцах 4 и 5 – двоичные комбинации Q1Q2, кодирующие состояние автомата, в которое он переходит в момент времени (t+1) под воздействием соответствующего входного сигнала.
Столбцы 6, 7 (q1 и q2) составляются в соответствии с таблицей переходов выбранного типа ЭА, в данном примере Т-триггера (табл. 5.24), и описывают функции возбуждения элементов памяти, которые необходимо сформировать для осуществления переходов синтезируемого автомата. Например, если при выполнении перехода из некоторого состояния ai в состояние aj первый ЭА должен изменить свое значение из Q1(t)=1 в Q1(t+1)=0, то в соответствии с табл. 5.24 на его входе в момент времени t должен быть сформирован сигнал q1=1.
Последние два столбца табл. 5.33 описывают выходные сигналы, формируемые синтезируемым автоматом Мили в момент перехода из одного состояния в другое. При синтезе автомата Мура последние два столбца не обязательны, поскольку его выходные сигналы однозначно определяются кодами состояний, в которых может находиться автомат.
В кодированной таблице переходов-выходов порядок заполнения строк, соответствующих переходам синтезируемого автомата, может быть произвольным. В некоторых случаях удобно упорядочить строки по какому-нибудь принципу. Например, в табл. 5.33 строки упорядочены по возрастанию двоичных кодов, соответствующих наборам сигналов (SQ1Q2), поступающих на входы КС автомата в момент времени t.
4. Задание и минимизация КС автомата.
По кодированной таблице переходов-выходов формируются функции выходов и функции возбуждения элементарных автоматов. В рассматриваемом автомате Мили функции возбуждения q1(t), q2(t) и функции выходов Z1(t), Z2(t) зависят от текущего состояния элементарных автоматов Q1(t), Q2(t) и от входного сигнала S(t).
Составляя по кодированной таблице переходов-выходов соответствующие логические выражения для функций возбуждения элементов памяти и функций выходов, получим следующую систему ПФ, описывающую комбинационную часть синтезируемого автомата:
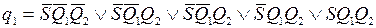 ;
;
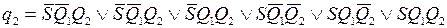 ;
;
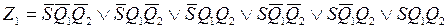
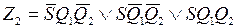 .
.
Ясно, что вышеприведенные функции следует минимизировать не по отдельности, а как систему ПФ (см. раздел 4.7). Однако это не всегда возможно вследствие ее громоздкости.
Для данного примера минимизированная система ПФ имеет вид
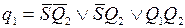 ;
;
 ;
;
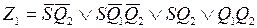
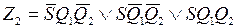 .
.
5. Построение функциональной (логической) схемы автомата.
Пусть в рассматриваемом примере синтез комбинационной части автомата производится в базисе И-ИЛИ-НЕ. Логическая схема синтезируемого автомата изображена на рис. 5.12. Сигнал «С» снимается с выхода генератора синхронизирующих импульсов.
Cтруктурный синтез цифрового автомата можно осуществлять с использованием некодированных входных и выходных сигналов.
Рассмотрим пример.
Осуществим структурный синтез автомата, заданного графом переходов, изображенным на рис. 5.13.

Пусть в качестве элементарных автоматов используются Т-триггеры, а для реализации комбинационной схемы используется логический базис И-ИЛИ-НЕ.
Для кодирования пяти состояний потребуются три двоичных разряда Q1, Q2, Q3. Закодируем состояния синтезируемого автомата в соответствии с табл. 5.34, а входные и выходные сигналы оставим в незакодированном виде.
Таблица 5.34
| a \ Q | Q1 | Q2 | Q3 |
Тогда кодированная таблица переходов-выходов может быть представлена в виде табл. 5.35.
Таблица 5.35
| Вх. сигнал | ai | Q1Q2Q3 | aj | Q1Q2Q3 | q1q2q3 | Вых. сигнал |
| – | 0 1 1 | 1 0 0 | 1 1 1 | 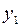
| ||
| – | 1 0 0 | 0 0 0 | 1 0 0 | 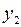
| ||
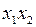
| 0 0 0 | 0 0 0 | 0 0 0 | 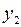
| ||
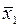
| 0 0 0 | 0 0 1 | 0 0 1 | 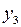
| ||
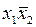
| 0 0 0 | 0 1 0 | 0 1 0 | 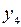
| ||
| – | 0 0 1 | 0 1 1 | 0 1 0 | 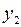
| ||
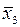
| 0 1 0 | 0 1 0 | 0 0 0 | 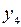
| ||
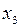
| 0 1 0 | 0 1 1 | 0 0 1 | 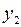
| ||
| t | t+1 | t |
Запишем функции выходов и функции возбуждения:
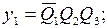
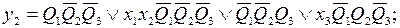
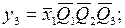
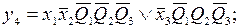
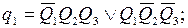

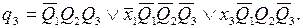
Введем следующие обозначения:
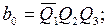
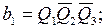

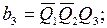
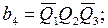
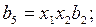


Тогда выражения для функций возбуждения и функций выходов могут быть записаны следующим образом:

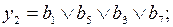
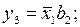
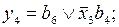
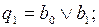
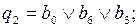

Функции b0, b1, b2, b3, b4 описывают дешифратор состояний. Для кодирования пяти состояний автомата использованы пять трехразрядных двоичных наборов. Остальные три набора являются несущественными и могут быть использованы для минимизации функций дешифрирования состояний. Воспользуемся картой Карно, в клетках которой записаны номера состояний, соответствующие выбранному варианту кодирования. Свободные ячейки можно использовать для минимизации кодов состояний:
| Q1 | Q2 | |||
 
| 
| 
| ||
| Q3 |
Таким образом, функции b0 – b4 примут вид
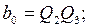



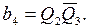
5.4. Рациональный выбор варианта
кодирования состояний синхронных автоматов
При выполнении структурного синтеза автомата можно показать, что сложность функций возбуждения и функций выходов существенно зависит не только от используемого типа элементарных автоматов, но и от выбранного варианта кодирования состояний.
Кодирование состояний абстрактного автомата, при котором получаются минимальные (в смысле необходимого для технической реализации оборудования) функции возбуждения и выходов, – процесс довольно сложный, связанный с перебором большого числа вариантов. Поэтому в дальнейшем остановимся на рассмотрении правил кодирования, приводящих, в большинстве случаев, к получению близких к минимальным (а иногда и к минимальным) схемам на элементах И, ИЛИ, НЕ, реализующим функции возбуждения элементов памяти синтезируемого автомата. Все дальнейшие рассуждения будем вести в предположении, что для кодирования состояний всегда будет использоваться минимально возможное число элементов памяти.
Рассмотрим абстрактный автомат, заданный таблицей переходов-выходов (табл. 5.36).
Таблица 5.36
| x \ a | |||
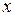
| 3,0 | 1,1 | 2,0 |
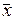
| 3,1 | 3,1 | 2,0 |
Пусть состояния автомата закодированы в общем виде в соответствии с табл. 5.37, где bijÎ{0, 1}.
Таблица 5.37
| a \ Q | Q1 | Q2 |
| b11 | b21 | |
| b12 | b22 | |
| b13 | b23 |
Составим кодированную таблицу переходов (табл. 5.38).
Таблица 5.38
| х | Q1 | Q2 | Q1 | Q2 |
| b11 | b21 | b13 | b23 | |
| b12 | b22 | b13 | b23 | |
| b13 | b23 | b12 | b22 | |
| b11 | b21 | b13 | b23 | |
| b12 | b22 | b11 | b21 | |
| b13 | b23 | b12 | b22 | |
| t | t | t+1 |
Пусть 
Условимся, что в качестве элементарных автоматов используются
D-триггеры, значения функций возбуждения которых, в соответствии с таблицей переходов, совпадают со значениями Q(t+1). Тогда функции возбуждения элементарных автоматов будут иметь вид
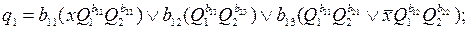
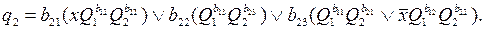
Приравнивание переменных bij к нулю или единице дает возможность оценить влияние на сложность схемы любого частного варианта кодирования.
Рациональный вариант кодирования выбирается таким образом, чтобы максимально упростить уравнения для q1 и q2. Для этого можно пользоваться двумя эмпирическими правилами.
1. Положить равными нулю переменные bij, которые в уравнениях для q имеют наиболее сложные сомножители (коэффициенты).
2. Переменным bij необходимо приписывать такие значения, чтобы ненулевые члены уравнений могли быть взаимно упрощены.
При использовании этих правил важно помнить, что каждому состоянию автомата должна соответствовать только одна кодовая комбинация.
В рассматриваемом примере в соответствии с первым правилом положим b13 = b23 = 0. Это приведет к тому, что в уравнениях для q1 и q2 последние слагаемые будут равны нулю и могут быть отброшены, а состояние автомата а3 будет кодироваться двоичным набором 00. Если теперь положить b11 = 0, то b21 = 1, так как кодовая комбинация 00 уже используется для кодирования состояния а3. Таким образом, состояние а1 кодируется двоичным набором 01. Для кодирования состояния а2 используем набор 10, что означает приравнивание к нулю переменной b22 и приравнивание к единице переменной b12.
Окончательно функции возбуждения примут вид
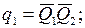
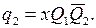
На основании приведенных выше правил и рассмотренного примера можно сделать вывод, что те состояния, в которые осуществляется большое число переходов, должны кодироваться наборами с минимальным числом единиц, а те состояния, между которыми имеются переходы, должны кодироваться наборами, отличающимися, по возможности, наименьшим количеством разрядов.
Вопросы для самоконтроля
1. Что представляет собой обобщенная схема ЦА? Какие компоненты включает и какие между ними установлены связи?
2. Какие модели и способы задания ЦА вам известны?
3. В чем состоит идея минимизации числа состояний абстрактного ЦА? Какие методы минимизации вам известны?
4. Каким условиям должен удовлетворять набор элементов для структурного синтеза ЦА?
5. Какие типы элементарных автоматов (триггеров) вам известны?
6. Каковы основные этапы структурного синтеза цифровых автоматов?
7. На что в автомате может повлиять выбор того или иного варианта кодирования его внутренних состояний?
Дата добавления: 2014-12-27; просмотров: 1453;
