Закономерности свободного падения частиц

Минеральная частица, падающая в какой-либо среде, обладает гравитационной силой. Характер падения тел в жидкой или газообразной среде определяется взаимодействием трех сил: силы тяжести, направленной вниз, подъемной (выталкивающей, архимедовой) силы, направленной вверх и силы сопротивления среды, направленной тоже вверх.

Сила тяжести зависит от плотности и объема твердого тела.

Подъемная сила – от объема тела и плотности среды.

Сила сопротивления среды– от режима движения (турбулентного или ламинарного) и слагается из сопротивления сил инерции (динамического) и сопротивления сил трения (вязкостного). Оба вида сопротивления среды движущемуся в ней телу действуют одновременно, но с неодинаковой силой.

Преобладание динамического сопротивления наблюдается при турбулентном движении и характерно для больших размеров движущихся частиц (2 мм и выше) и больших скоростей движения.

Преобладание вязкостного сопротивления наблюдается при ламинарном движении (характерно для движущихся частиц небольшого размера – 0,1 мм и ниже) и небольших скоростях движения, а также при высоких значениях вязкости среды.

Для частиц промежуточной крупности (от 0,1 до 2 мм) характерен переходных режим, при котором наблюдается действие обоих видов сопротивления.

Параметр, характеризующий режим течения жидкости, называется числом Рейнольдса (Re). При значениях Re ≥ 1000 течение жидкости турбулентное, при Re ≤ 1 – ламинарное и при Re = 1000- 1 режим течения жидкости промежуточный.

Начальный момент движения тела в среде характеризуется нулевым значением скорости его движения и максимальным значением ускорения. В дальнейшем, по мере возрастания скорости падения тела, увеличивается сила сопротивления среды, ускорение уменьшается и за короткий промежуток времени эта сила достигает величины движущей силы. В этот момент падающее тело достигает своей предельной (максимальной) скорости. Скорость становится постоянной, ускорение равно 0. Конечная или постоянная скорость обозначается υ₀.

Разница в конечных скоростях падения различных минеральных частиц в основном определяет процесс их разделения при классификации и гравитационном обогащении.

Для определения скорости свободного падения υ₀ (м/с) частиц крупности 0,1 мм и ниже можно пользоваться уравнением Стокса (для воды):

υ₀= 0,545d²(δ-1000)/μ, м/сек

где d – диаметр частицы, м;

δ – плотность частиц, кг/м³;

Δ – плотность среды, кг/м³;

μ – коэффициент вязкости, Н·с/м² (для воды μ = 0,001; для воздуха μ = 0,000018).

Для воздуха уравнение Стокса:

υ₀= 30 278d²(δ-1,23), м/сек.

Более крупные зерна имеют другую формулу для определения скорости свободного падения. Для частиц крупностью 2 мм и выше используется уравнение Риттингера:

для воды

;

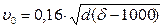для воздуха

.

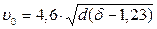Для частиц крупностью 0,1-2 мм Алленом выведены другие уравнения:

для воды

;

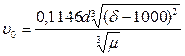для воздуха

.

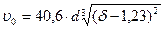Все эти формулы выведены для частиц идеальной (шарообразной) круглой формы. Для частиц неправильной формы υ₀´ < υ₀. Это влияние учитывается эмпирическими коэффициентами К. Например в формуле Риттингера К_R равно: для частиц пластинчатой формы – 22,7

угловатой - 33,4

продолговатой - 35,8

округлой - 42,2