Строение и фазовый состав почвы.

{

int a[5] = {5,1,7,41,2};

list <int> L(a,a+5);

list<int>::iterator ff = L.begin();

for (ff = L.begin();ff != L.end();ff++)

cout <<*ff <<" " ;

L.sort();

cout << "\n\nSort - >";

for (ff = L.begin();ff != L.end();ff++)

cout<<*ff <<" " ;

cout<<"\nmax = " <<*max_element(L.begin(),L.end());

cout<<"\nSumma = " <<accumulate(L.begin(),L.end(),0);

vector<char*> rgs;

rgs.push_back("aaa");

rgs.push_back(" bbb");

rgs.push_back(" ccc");

cout<<"\nConc -> "<<accumulate(rgs.begin(),rgs.end(),

string(" nnn ")) << endl;

}

Результат виконання програми:

5 1 7 41 2

Sort - >1 2 5 7 41

max = 41

Summa = 56

Conc -> nnn aaa bbb ccc

Алгоритм inner_product.

Перша форма алгоритму inner_product використовується для обчислення скалярного добутку двох послідовностей (скалярним добутком послідовностей а і b є вираз 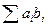). Початкове значення добутку задається четвертим параметром. Тип цього параметра визначає тип результату (функція повертає обчислений добуток):

template t<class In1, class In2, class Т>

Т inner_product(Inl first1, Inl last1,

In2 first2, T init);

Друга форма алгоритму inner_product використовується для виконання над двома послідовностями дій, заданих за допомогою двох функцій або функціональних об'єктів. Перший використовується замість операції додавання, другої, – замість множення:

template t<class In1, class In2, class Т,

class BinOp1, class BinOp2>

T inner_product(In1 first1, In1 last1, In2 first2,

T init, BinOp1 binary_op1, BinOp2 binary_op2);

Наступний виклик обчислює добуток сум відповідних елементів послідовностей а і b:

cout << inner__product(a, а + m, b, mu1,

multiplies<int>(), plus<int>());

Алгоритм partial_sum.

Алгоритм partial_sum формує послідовності з часткових сум елементів. Наприклад, для послідовності чисел 3 1 2 3 5 результатом буде 3 4 6 9 14, тобто кожен елемент результату дорівнює попередньому елементу, збільшеному на поточний елемент початкової послідовності.

Замість суми четвертим параметром можна задати іншу операцію. Результат можна помістити і в початкову послідовність, для цього третім параметром вказується ітератор на її початок. Функція повертає ітератор на елемент, наступний за останнім результуючої послідовності.

template t<class In, class Out>

Out partial_sum(In first, In last, Out result);

template t<class In, class Out, class BinOp>

Out partial_sum(In first, In last, Out result,

BinOp binary_op);

Алгоритм adjacent_difference.

Алгоритм adjacent_difference виконує обчислення різниці між суміжними елементами, тобто d_i = a_i – a_i-1. Замість різниці четвертим параметром можна задати іншу операцію. Функція повертає ітератор на елемент, наступний за останнім результуючої послідовності.

template t<class In, class Out>

Out adjacent_difference(In first,In last,Out result);

template t<class In, class Out, class BinOp>

Out adjacent_difference(In first,In last,Out result,

BinOp binary_op);

Цей алгоритм є зворотним попередньому, тобто виклик для однієї і тієї ж послідовності спочатку одного, а потім іншого алгоритму приведе до початкової послідовності.

Завдання

Виконати завдання за допомогою використання контейнерів та алгоритмів.

Перелік варіантів завдань:

Варіант 1

Визначити добуток додатних парних чисел масиву B(n). Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Додатних парних елементів в масиві немає".

Варіант 2

Визначити добуток від’ємних чисел масиву A(n), що стоять на парних позиціях. Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Від’ємних елементів в масиві немає".

Варіант 3

Визначити суму і кількість непарних чисел масиву М(n). Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Непарних елементів в масиві немає".

Варіант 4

У масиві чисел K(n) визначити суму і кількість чисел, кратних 5. Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Елементів кратних 5 в масиві немає".

Варіант 5

У масиві чисел X(n) визначити кількість чисел, кратних 2, і чисел, не кратних 3. Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Чисел, кратних 2 і чисел не кратних 3 в масиві немає".

Варіант 6

Є масив чисел C(n), визначити кількість і добуток елементів масиву, які знаходяться в діапазоні 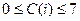. Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Елементів з діапазону [0; 7] в масиві немає".

Варіант 7

У заданому масиві А(n) визначити середнє арифметичне значення чисел, кратних трьом. Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Елементів кратних 3 в масиві немає".

Варіант 8

Визначити середнє арифметичне значення елементів масиву F(n), які задовольняють вимозі 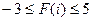. Якщо таких елементів немає, вивести на екран дисплея повідомлення: "Елементів, що задовольняють вимозі, в масиві немає".

Варіант 9

У числовому масиві А(n) визначити мінімальний елемент масиву і його порядковий номер. Результат вивести на екран дисплея.

Варіант 10

Визначити мінімальний елемент числового масиву K(n) і кількість елементів, рівних мінімальному елементу. Вивести на екран дисплея результат.

Варіант 11

Визначити добуток непарних елементів масиву P(n), що стоять на парних позиціях. Якщо таких елементів немає, на екран дисплея вивести повідомлення: "Непарних елементів, що стоять на парних позиціях в масиві немає".

Варіант 12

Визначити середнє арифметичне значення елементів масиву B(n), кратних восьми. Якщо таких елементів немає, на екран дисплея вивести повідомлення: "Елементів кратних 8 в масиві немає".

Варіант 13

У числовому масиві Z(n) серед додатних елементів визначити максимальний елемент масиву. Вивести на екран дисплея результат.

Варіант 14

Визначити кількість від’ємних елементів в масиві А(n) і на їх місце записати нулі. Якщо таких елементів немає, на екран дисплея вивести повідомлення: "Від’ємних елементів в масиві немає".

Варіант 15

Визначити добуток додатних елементів масиву і їх кількість. За відсутності додатних чисел вивести на екран дисплея "Додатних чисел в масиві немає".

Варіант 16

Обчислити кількість елементів цілочисельного масиву V(n), кратних семи. За відсутності таких елементів вивести на екран дисплея "Елементів, кратних 7, немає".

Варіант 17

Для числового масиву Z(n) визначити середнє арифметичне значення мінімального і максимального елементів. Результат вивести на екран дисплея.

Варіант 18

Для заданого масиву А(n) обчислити суму і кількість елементів, що задовольняють умові 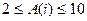. Результат вивести на екран дисплея.

Варіант 19

Визначити суму і добуток додатних чисел, що стоять на парних позиціях в масиві В(n). Результат вивести на екран дисплея.

Варіант 20

У масиві C(n) визначити середнє арифметичне значення додатних елементів і середнє арифметичне значення від’ємних елементів. Результат вивести на екран дисплея.

СПИСОК ЛІТЕРАТУРИ

1. Стивен Поттс, Тиноти С. Монк. Borland C++. (Минск, Попурри, 1996г. – 741 с.

2. Р. Уинер. Язык Турбо С. – М.: Мир, 1991г. - 384 с.

3. Секунов Н.Ю. Самоучитель Visual C++ 6. – СПб.: БХВ – Санкт-Петербург, 1999. – 960 с.

4. Шилдт Г. Самоучитель С++, 3-е издание. – СПб.: BHV – Санкт-Петербург, 1998. – 688 с.

5. Фейсон Т. Объектно-ориентированное программирование на Borland C++ 4.5. – К.: "Диалектика", 1996. – 544 с.

6. Страуструп Б. Язык программирования C++. – СПб.: БИНОМ, 1999. – 991 с.

7. Страуструп Б. Дизайн и эволюция языка C++. – М.: ДМК, 2000. – 448 с.

8. Мейерс С. Эффективное использование C++. – М.: ДМК, 2000. – 240 с.

9. Лаптев В.В., Морозов А.В., Бокова А.В. С++. Объектно-ориентированное программирование. Задачи и упражнения. – СПб.: Питер, 2007. – 288 с.

10. Павловская Т.А. С/С++. Программирование на языке высокого уровня. – СПб.: Питер, 2003. – 461 с.

Строение и фазовый состав почвы.

Почва – не сплошная однородная масса, а трехфазная дисперсная среда, состоящая из твердых, жидких, газообразных частиц, раздробленных и перемешанных между собой.

Почва состоит из: твердых, жидких, газообразных частиц, а также фаз и живых частиц (растительных остатков и микроорганизмов).

Основные физ. св-ва:

· Скважность – отношение объема пустот к общему объему почвы в %.

· Плотность (Объемная масса) – отношение массы почвенного образца к его объему.

· Влажность почвы. Абсолютная влажность и относительная влажность:

W_a = (100(m-m_c))/m_c

W₀ = 100*W_a/W_п

, где W_п – полевая влагоемкость, % - свойство почвы принимать и задерживать влагу и не позволять ей стекать. Физическая спелость почвы соответствует W_a = 15 – 30 %

· Гранулометрический состав – относительное содержание первичных элементарных частиц разного размера, которые делятся на фракций: камни, гравии, песок, пыль. Физическая глина и физический песок – классиф-ция почв по гранул-кому составу. В зависимости от содержания физ. глины: глинистые, суглинистая, песчаная, супесчаная.

· Структурность: бесструктурные (песчаные), глинистые сплошные, глинистые с агрегатной структурой.