Орбиты искусственных спутников Земли

Орбита космического аппарата (рис. 2.7) – это его путь в поле центральной силы, определяемый воздействием силы тяготения, при этом сам космический аппарат считается бесконечно малым телом, масса которого настолько мала по сравнению с массой цент­рального тела, что его можно считать притягиваемым централь­ным телом, но не притягивающим последнее. Поле притягива­ющей силы определяют обычно как поле тяготения, создавае­мое однородным и сферическим телом. Применительно к ИСЗ таким телом является Земля с ее полем тяготения.

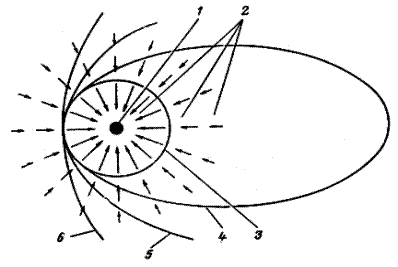
Рис. 2.7. Орбиты космического аппарата в поле центрального тела:

1 — центральное тело;

2— силовое поле центрального тела;

3— круговая орбита;

4 — эллиптическая орбита;

5 — параболическая орбита; 6— гиперболическая орбита

Силовое поле центральной силы сферически симметрично и сила притяжения в каждой его точке направлена по радиусу к центру притяжения (рис. 2.7 величина стрелок показы­вает увеличение силы тяготения при приближении к центру массы центрального тела по закону, обратно пропорциональ­ному квадрату расстояния).

Из материала лекции 1 нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. В данном случае нас будут интересовать только два из них – первый и третий.

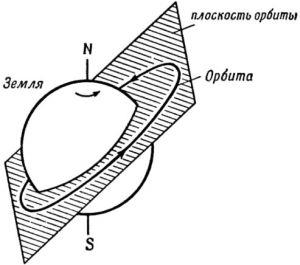
Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (рис. 2.8). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит – эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.

Рис. 2.8. Орбита ИСЗ

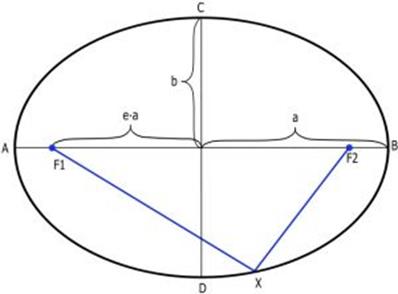Элементы эллипса показаны на рис. 2.9. F1 и F2 – фокусы эллипса; a – большая полуось; b – малая полуось; е – эксцентриситет эллипса, который определяется следующим образом:

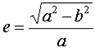
Таким образом, первое важное положение – ИСЗ движутся вокруг Земли по эллипсам.

Согласно третьему закону Кеплера, квадраты периодов обращения T спутников относятся как кубы их больших полуосей

a:

Рис. 2.9. Элементы эллипса

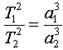
В наиболее общем случае урав­нение траектории движения КА является уравне­нием движения свободного тела в поле центральной силы, которое в полярных координатах имеет вид уравнения конического сечения (рис. 2.10):

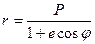, (2.1)

где 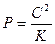– параметр конического сечения;

e =PC₁ – эксцентриситет конического сечения;

С и С₁ – постоянные интегрирования.

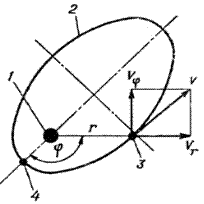
Рис. 2.10. Движение КА в поле центральной силы Земли:

1 — центральное тело (Земля); 2 — орбита КА;

3 — КА; 4 — перигей орбиты; r — радиус-вектор КА;

V — суммарная скорость; V_r — радиаль­ная скорость;

V_φ — трансверсальная скорость

Уравнение (2.1) является урав­нением кривой второго порядка, для которого конкретная форма опреде­ляется значением эксцентриситета е = 0 для окружности, е < 1для эллипса (рис. 2.11), е = 1 для параболы, е > 1 для гиперболы.

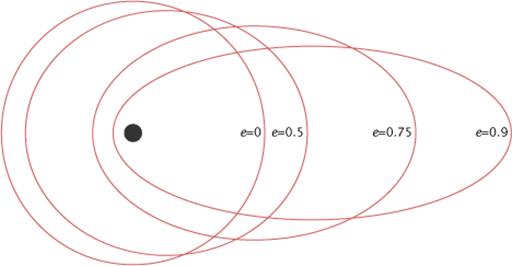
Рис. 2.11. Изменение вида эллиптической орбиты при увеличении значения

эксцентриситета

Завершающей стадией полета ракеты-носителя является вывод КА на орбиту, форма которой опре­деляется величиной кинетической энергии, сообщаемой косми­ческому аппарату ракетой-носителем, т. е. величиной конечной скорости последней. При этом величина кинетической энергии сообщаемой КА, должна находиться в опре­деленном отношении к величине энергии поля центрального тела, которая существует на данном расстоянии r от его цент­ра. Это отношение характеризуется постоянной энергии h,пред­ставляющей разность энергии поля центрального тела и кине­тической энергии космического аппарата, находящегося в сво­бодном движении в этом поле на расстоянии r от его цент­ра, т. е.

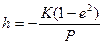. (2.2)

В зависимости от величины эксцентриситета е постоянная 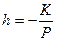для окружности, h < 0 для эллипса, h = 0 для пара­болы и h > 0 для гиперболы.

Конечная скорость ракеты-носителя, обеспечивающая выведе­ние космического аппарата на орбиту в поле земного тяготения,

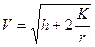. (2.3)

Анализ величин постоянной энергии h, соответствующих раз­личным формам орбиты космического аппарата, и зависимости (2.3) позволяет установить значения конечных скоростей ракеты-носителя, обеспечивающих полет КА в поле земного тяготения по той или иной орбите.

Конечная скорость РН должна быть равна 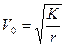для выведения КА на круговую ор­биту, 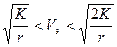— на эллиптическую, 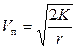— на параболическую и 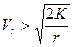— на гиперболическую.

Применительно к круговым орбитам со значениями r,близ­кими к радиусу Земли R = 6 371 км, конечная скорость ракеты-носителя для выведения космическою аппарата на круговую орбиту V₀ ~ 7900 м/с. Это так называемая первая космиче­ская скорость. Для эллиптических орбит конечные скорости V_э = 7 900 … 11 200 м/с.

Космические аппараты, движущиеся по круговым и эллип­тическим орбитам, находятся в поле земного тяготения и имеют ограниченное время существования. Наличие остатков атмо­сферы и прочих частиц материи приводит со временем к умень­шению скорости космических аппаратов, сообщенной им ра­кетой-носителем, а торможение в силовом поле Земли вызы­вает их вход в плотные слои атмосферы и разрушение. Основ­ным фактором, определяющим время жизни КА на круговой и эллиптической орбитах, является высота первой и высота перигея второй, где происходит основное тор­можение.

Полет космического аппарата по параболе с энергетической точки зрения характеризуется так называемой второй кос­мической скоростью, равной V_п ≈ 11 200 м/с, которая по­зволяет преодолеть земное притяжение. Движение по параболе относительно Земли возможно только в случае отсутствия лю­бых сил воздействия, кроме силы земного тяготения.

Гиперболические орбиты характеризуются скоростями V_г > 11 200 м/с, среди которых представляет интерес так на­зываемая третья космическая скорость, равная V_г ≈ 16 700 м/с, — наименьшая начальная скорость, при ко­торой КА может преодолеть не только земное, но и солнечное притяжение и покинуть Солнечную систему.

Гиперболические орбиты в теории космических полетов имеют место при переходе космического аппарата из поля тяго­тения одного центрального тела в поле тяготения другого, при этом космический аппарат как бы вырывается из одной гра­витационной зоны и входит в другую.

Как правило, РН сообщают космическому ап­парату только первую космическую скорость и выводят его или на круговую, или на эллиптическую орбиту. Достижение второй и третьей космических скоростей более выгодно за счет энер­гетики самого КА, стартующего в этом слу­чае с опорной орбиты ИСЗ.