Усилители с двухконтурным фильтром
В приемных устройствах применяются различные варианты усилителей с двухконтурными фильтрами. Наиболее распространены индуктивная и внешнеемкостная связи между контурами. Связь контуров с усилительными приборами обычно бывает автотрансформаторная или с помощью емкостного делителя.
Рассмотрим вариант с индуктивной связью между контурами(Рис. 6.5). Основные выводы при этом будут справедливы и для других вариантов.
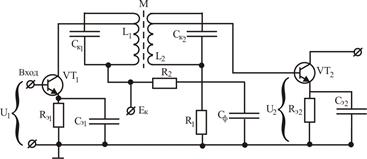
Рис.6. 5
Перейдем к эквивалентной схеме, в которой выход усилительного прибора заменим генератором тока  с проводимостью
с проводимостью  и емкостью
и емкостью  , а вход следующего каскада заменим проводимостью
, а вход следующего каскада заменим проводимостью  и емкостью
и емкостью  . Эквивалентная схема показана на Рис. 6.6, где
. Эквивалентная схема показана на Рис. 6.6, где  ,
,  - полные емкости;
- полные емкости;
 ,
,  - полные проводимости.
- полные проводимости.
На основании теоремы об эквивалентном генераторе заменим генератор тока  генератором ЭДС
генератором ЭДС  (Рис. 6.7), которая находится как напряжение холостого хода между точками 1-1:
(Рис. 6.7), которая находится как напряжение холостого хода между точками 1-1:  . Зная
. Зная
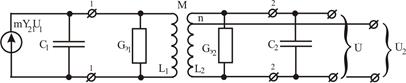 Рис.6. 6
Рис.6. 6
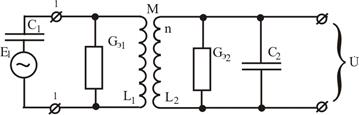 Рис.6. 7
Рис.6. 7
|
коэффициент передачи фильтра  , можно найти коэффициент усиления
, можно найти коэффициент усиления
 , (6.17)
, (6.17)
где  - характеристическое сопротивление первого контура.
- характеристическое сопротивление первого контура.
Выражение (6.17) справедливо для усилителя с фильтром, содержащим любое число контуров (при соответствующем  ).
).
Фазочастотная характеристика усилителя определяется фазочастотными характеристиками фильтра и усилительного прибора. В отличие от одноконтурного усилителя она в данном случае имеет дополнительный фазовый сдвиг на  . Модуль коэффициента усиления имеет вид:
. Модуль коэффициента усиления имеет вид:
 . (6.18)
. (6.18)
Вблизи резонанса (  ) частотная характеристика усилителя в основном определяется частотной характеристикой фильтра:
) частотная характеристика усилителя в основном определяется частотной характеристикой фильтра:
 . (6.19)
. (6.19)
Из теории линейных цепей известны выражения для  . Для днухконтурного фильтра при одинаковых параметрах контуров
. Для днухконтурного фильтра при одинаковых параметрах контуров
 , (6.20)
, (6.20)
где  .
.
С учетом выражения (6.20) выражение (6.19) имеет вид
 . (6.21)
. (6.21)
В N-каскадном усилителе коэффициент усиления
 . (6.22)
. (6.22)
При резонансе ( 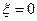 )
)
 . (6.23)
. (6.23)
Из (6.22) и (6.23) выражение частотной характеристики усилителя, если усилительный прибор выбран с достаточным запасом по частоте, имеет вид
 . (6.24)
. (6.24)
Форма характеристики зависит от 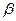 . При
. При 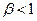 она одногорбая; при
она одногорбая; при 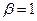 (критическая связь) частотная характеристика имеет наиболее ровную вершину; при
(критическая связь) частотная характеристика имеет наиболее ровную вершину; при 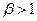 она двугорбая.
она двугорбая.
Частоотная характеристика наиболее близка к прямоугольной, когда впадина между двумя горбами соответствует допустимой неравномерности в пределах полосы пропускания. Для настройки удобнее фильтры с критический связью между контурами ( 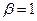 ). При этом и фазовая характеристика ближе к линейной.
). При этом и фазовая характеристика ближе к линейной.
Дата добавления: 2014-12-26; просмотров: 1540;
