Магнитное поле прямолинейного проводника с током
Суммируя все 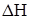 от всех
от всех 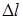 , на основе уравнения (11) получаем:
, на основе уравнения (11) получаем:
 . (12)
. (12)
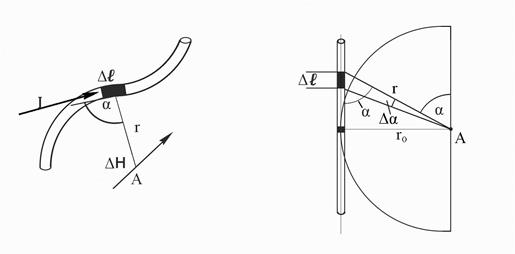
Согласно рис. 5, б имеем: 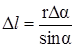 и
и 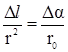 . Тогда
. Тогда  . Переходя к интегрированию, получаем:
. Переходя к интегрированию, получаем:  .
.
Таким образом, напряженность поля Н в любой точке, расположенной на расстоянии r от оси прямолинейного проводника, определяют по формуле, А/м:
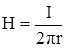 . (13)
. (13)
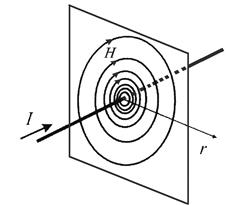
Силовые линии магнитного поля – это концентрические окружности с центрами на оси проводника (рис. 6, а). Направление поля связано с направлением тока правилом правозаходного винта. По мере приближения к оси проводника (  ) поле усиливается, а с удалением – падает, что показано на рис. 6, а сгущением или, соответственно, разряжением силовых линий.
) поле усиливается, а с удалением – падает, что показано на рис. 6, а сгущением или, соответственно, разряжением силовых линий.
а б
Рис. 5. Иллюстрации к выводу закона Био-Савара-Лапласа
для элемента с током: а – в произвольном контуре;
б – в прямолинейном проводнике
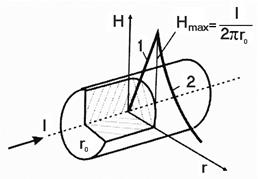
Подчеркнем, что гиперболический закон (13) уменьшения Н верен только для точек вне проводника. Внутри проводника диаметром 2r0 поле по мере удаления от его геометрической оси линейно возрастает с увеличением r по закону:
 . (14)
. (14)
Таким образом, напряженность поля внутри проводника в пределах r < r0(участок 1) линейно зависит от r, т. е.  , а вне – при r > r0 (участок 2) –
, а вне – при r > r0 (участок 2) – 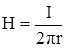 (рис. 6, б). Напряженность в любой точке, расположенной на поверхности проводника (r = r0), достигает максимального значения
(рис. 6, б). Напряженность в любой точке, расположенной на поверхности проводника (r = r0), достигает максимального значения 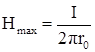 .
.
Прямолинейные проводники с током в виде медных стержней или гибких кабелей различного сечения применяют для циркулярного намагничивания контролируемых деталей.
а б
Рис. 6. Магнитное поле прямолинейного проводника с током:
а – линии магнитного поля; б – напряженность поля внутри и
вне проводника
Дата добавления: 2014-12-26; просмотров: 1188;
