Р. А. Ахмеджанов

Содержание

Часть I: Теория

Глава 1: Как движутся ИСЗ?

§ 1. Законы Кеплера и типы орбит

§ 2. Орбитальные элементы

§ 3. Круговая орбита

§ 4. Эллиптическая орбита

§ 5. Эволюция орбиты ИСЗ

Прецессия орбиты

Вращение эллиптической орбиты

Атмосферное торможение

Давление света

[Глава 2: Какие орбиты и ИСЗ бывают]

Часть II: Практика

[Глава 3: Подготовка к наблюдениям]

[Глава 4: О времени]

[Глава 5: Что и как наблюдать?]

[Приложения]

[Использованные источники]

[Полезные ресурсы сети INTERNET] Глава 1: Как движутся ИСЗ?

Перед тем, как приступить к рассмотрению вопросов наблюдения ИСЗ, нужно выяснить как они движутся - по каким орбитам и каковы характеристики этих орбит. Без понимания этих вопросов наблюдение ИСЗ превращается в охоту за неведомым зверем, который неизвестно где обитает...

§ 1. Законы Кеплера и типы орбит

Из курса средней школы нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. Нас будут интересовать только два из них - первый и третий.

Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (см. рис. 2). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит - эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.

Рис. 1. Орбита ИСЗ. [1]

Элементы эллипса показаны на рис. 2. "F1" и "F2" - фокусы эллипса; "a" - большая полуось; "b" - малая полуось; "е" - эксцентриситет эллипса, который определяется следующим образом:

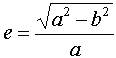, (1)

Таким образом, первое важное положение - ИСЗ движутся вокруг Земли по эллипсам.

Согласно третьему закону Кеплера, квадраты периодов обращения "T" спутников относятся как кубы их больших полуосей "a":

, (2)

Рис. 2. Элементы эллипса. [2]

§ 2. Орбитальные элементы

Для того, чтобы задать параметры и ориентацию орбиты ИСЗ в пространстве, нужно указать 6 т.н. кеплеровских элементов (орбитальных элементов) (см. рис. 3):

Большая полуось "a". Равна среднему расстоянию ИСЗ от центра Земли.

Эксцентриситет "e" (см. формулу 1) - мера сплюснотости эллипса.

Наклонение орбиты "i" к экваториальной плоскости Земли - угол пересечения плоскости орбиты ИСЗ с плоскостью экватора Земли. Отсчитывается против часовой стрелки, если смотреть со стороны восходящего узла орбиты. Измеряется от 0° до 180°. Если наклонение не более 90°, то движение спутника считается прямым, если более 90° - то обратным.

Аргумент перигея (АП) ω - угол, отсчитываемый в плоскости орбиты ИСЗ от восходящего узла орбиты до точки перигея (точка, где расстояние между ИСЗ и центром Земли наименьшее). Угол отсчитывается против часовой стрелки, если смотреть с северного полюса мира. Линия, соединяющая восходящий и нисходящий узлы называется линией узлов.

Долгота восходящего узла (ДВУ) Ω - угол, отсчитываемый в плоскости земного экватора от восходящего узла до точки весеннего равноденствия. Угол отсчитывается против часовой стрелки, если смотреть с северного полюса мира.

Средняя аномалия (СА) M0 - угол, отсчитываемый в плоскости орбиты ИСЗ от перигея до ИСЗ на орбите. Угол отсчитывается против часовой стрелки, если смотреть с северного полюса мира.

Рис. 3. Орбитальные элементы. [2]

Итак, наше второе важное положение - орбита ИСЗ полностью задаётся шестью орбитальными элементами.

§ 3. Круговая орбита

Рассмотрим частный случай эллиптической орбиты - круговая орбита. Если значение эксцентриситета орбиты ИСЗ е = 0, то орбита представляет собой окружность с центром в центре Земли.

Для того, чтобы тело стало спутником Земли, оно должно обладать определённой скоростью при полёте вокруг неё. Если бы у Земли не было атмосферы, то минимальная скорость, необходимая для того, чтобы тело двигалось по окружности вокруг Земли, равна vк0 = 7,91 км/с. Но в реальности такого быть не может - спутник будет сильно тормозится в атмосфере Земли. Если ИСЗ начнёт двигаться на высоте менее примерно 160 км от поверхности Земли, то он сможет сделать лишь пару оборотов, после чего начнёт необратимо терять скорость и сгорит в плотных слоях атмосферы. Для примерного расчёта скорости ИСЗ на круговой орбите можно воспользоваться формулой [1]:

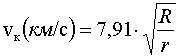, (3)

где R = 6371 км - средний радиус Земли, r = R + h - расстояние от центра Земли до ИСЗ, h - высота ИСЗ над поверхностью Земли. При наблюдениях важно знать период обращения ИСЗ Т - время, необходимое на один полный оборот вокруг Земли. Для круговой орбиты период Т можно вычислить по формуле [1]:

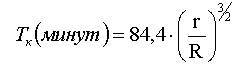, (4)

Из (4) видно, что минимальное время, необходимое ИСЗ для одного оборота, равно Tк0 = 84,4 минуты - при нулевой высоте над поверхностью. Никакое тело не может быстрее обогнуть поверхность Земли. При примерных оценках периода обращения ИСЗ по круговой орбите полезно помнить, что период обращения увеличивается примерно на 1 минуту при увеличении высоты ИСЗ на каждый 50 км. Этой оценкой можно пользоваться для ИСЗ не выше 1000 км.

Наше третье важное положение - ИСЗ не может двигаться долгое время по орбите вокруг Земли ниже 140-160 км. При этом, период обращения по круговой орбите является минимальным и для диапазона высот 160-1000 км изменяется всего с 87,6 до 105 минут.

§ 4. Эллиптическая орбита

Теперь рассмотрим общий вид орбиты ИСЗ - эллиптическая орбита (см. рис. 4). Как было указано выше, из первого закона Кеплера следует, что в фокусе эллиптической орбиты будет находится Земля (З), вокруг которой вращается ИСЗ. Двигаясь по эллиптической орбите, ИСЗ ближе всего подлетает к центру Земли в точке "П" - в перигее, а дальше всего находится в точке "А" - в апогее. Линия, соединяющая перигей и апогей называется линией апсид. Из наблюдений ИСЗ можно определить большую полуось и эксцентриситет орбиты, из которых можно вычислить значения перигейного "q" и апогейного "Q" расстояний:

. (5)

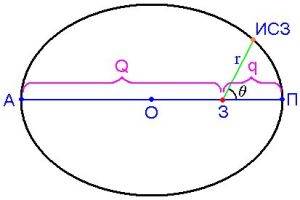Рис. 4. Перигей и апогей.

Из (5) видно, что Q + q = 2a. При движении по орбите изменяется расстояние "r" от Земли до ИСЗ - величина радиус-вектора "r" задаётся выражением [3]:

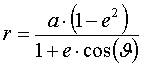. (6)

Скорость ИСЗ в любой точке эллиптической орбиты задаётся выражением [2]:

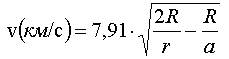. (7)

Период обращения для спутника на эллиптической орбите вычисляется по формуле (4), в которой вместо "r" нужно подставить значение большой полуоси "a".

Наше четвёртое важное положение - скорость движения ИСЗ по эллиптической орбите не равномерна: максимальна она в перигее, а минимальна в апогее. Период обращения теперь определяется не только большой полуосью "a", но и значением эксцентриситета "e".

§ 5. Эволюция орбиты ИСЗ

В этом параграфе мы рассмотрим, как изменяются параметры реальной орбиты ИСЗ под воздействием определённых факторов.

Прежде всего следует отметить следующее: если бы Земля имела форму идеального шара с равномерным распределением вещества, была лишена атмосферы, а Луна и Солнце отсутствовали бы, то ИСЗ вечно бы вращался по своей орбите, ориентация которой в пространстве не изменялась. Если бы спутник совершал 14 оборотов в сутки (при этом его период равен примерно 103 минуты), то за время одного витка ИСЗ Земля повернётся на 1/14 полного оборота (это примерно 26°). Это означает, что с каждым новым траектория ИСЗ смещалась к западу на 26° за каждый виток.

Прецессия орбиты

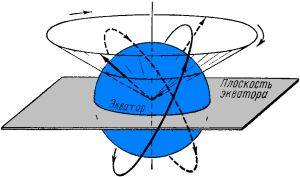В реальности форма Земли - геоид, полярный радиус которого RП = 6356,8 км, а экваториальный - RЭ = 6378,2 км, т.е. экваториальный радиус больше полярного на 21,4 км. Земля имеет экваториальный "горб", который своей массой оказывает влияние на движение ИСЗ. Влияние это не такое уж явное - масса "горба" не вызывает изменения наклонения "i" орбиты за счёт притягивания плоскости орбиты к плоскости экватора, как можно было бы ожидать - плоскость орбиты медленно поворачивается вокруг земной оси в направлении, противоположном вращению ИСЗ (см. рис. 5).

Рис. 5. Прецессия орбиты ИСЗ [4].

Этот процесс называется прецессией. Угол прецессии плоскости орбиты ИСЗ остаётся неизменным. Угловая скорость прецессии "X1" (градусов в сутки) определяется, в основном, наклонением орбиты [1]:

, (8)

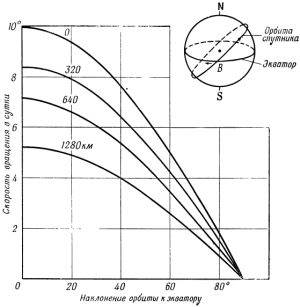где "i" - наклонение орбиты, "e" - эксцентриситет, RЭ - экваториальный радиус Земли, "а" - большая полуось орбиты ИСЗ. Если спутник движется в запада на восток, орбита поворачивается с востока на запад. Чем меньше наклонение ИСЗ, тем больше значение прецессии (см. рис. 6). Если спутник вращается с востока на запад (обратное движение ИСЗ), то прецессия орбиты происходит в обратную сторону. При этом линия узлов также поворачивается (см. рис. 7).

Рис. 6. Скорость вращения плоскости орбиты ИСЗ за счёт прецессии. Числа у кривых указывают значение большой полуоси [1].

Рис. 7. Смещение восходящего узла за один виток [4].

Теперь посмотрим, к каким изменениям условий наблюдения спутника приводит прецессия. Как известно, Земля делает полный оборот за 23ч56м4,09с (звёздные сутки) - за 24ч (средне-солнечные сутки) небо нам кажется повернувшимся на 361° (т.к. звёздные сутки короче средне-солнечных на 4 минуты - за это время небо повернётся на 1°). Если бы плоскость орбиты ИСЗ не прецессировала, то через 24ч он появлялся бы на небе на 1° западнее, чем накануне (если движение ИСЗ прямое). Но за счёт прецессии орбита поворачивается на Х1 градусов за сутки, поэтому ИСЗ через 24ч окажется на Х1 + 1 градус западнее (при обратном движении - на 1 - Х1 градус к западу). Период обращения спутника не кратен целой части суток. Если через сутки спутник будет пересекать ту же широту Земли на n минут позже, он окажется ещё на n/4 градусов западнее, т.к. за 1 минуту Земля поворачивается на 1/4 минуты. Следовательно, суммарный суточный сдвиг к западу составит (Х1 + 1 + n/4) градусов [1].

Вращение эллиптической орбиты

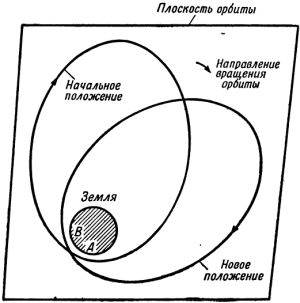Следующим важным эффектом, влияющим на эволюцию орбиты ИСЗ, является поворот плоскости эллиптической орбиты. Эффект этот, как и предыдущий, обязан своим существованием экваториальному "горбу" Земли, но в отличие от прецессии, действует только на эллиптичные орбиты. Эффект заключается в том, что эллиптическая орбита постоянно поворачивается в своей плоскости вперёд для спутников с нулевым наклонением, и назад - для спутников с наклонением, близким к 90°. За счёт этого точки перигея движутся вперёд или назад по орбите (см. рис. 8).

Рис. 8. Поворот эллиптической орбиты [1].

Скорость вращения "X2" эллиптической орбиты определяется выражением [1]:

. (9)

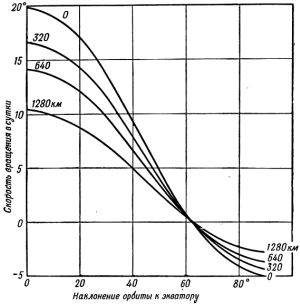На рис. 9 показаны графики зависимости X2(i) для ИСЗ с разными значениями больших полуосей "a".

Рис. 9. Скорость вращения X2 эллиптической орбиты [1].

Вращение происходит в том же направлении, что и движение спутника, если наклонение i < 63,4°, и в обратном направлении, если i > 63,4°. При i = 63,4° поворот орбиты отсутствует.

Наше пятое важное положение - движение ИСЗ подвержено возмущениям из-за несферичности Земли. За счёт прецессии орбита спутника может смещаться с угловой скоростью до 9°/сутки, а за счёт поворота эллиптической орбиты - до 15°/сутки. При этом, чем меньше наклонение, тем сильнее оба эффекта, но действовать они могут как в одну сторону, так и в противоположные.

Атмосферное торможение

Прецессия орбиты и поворот её плоскости связаны с действием несферичности Земли. Но кроме этого Земля окружена атмосферой, которая прослеживается до 2000 км над её поверхностью. Из этого следует, что на движение ИСЗ, особенно на низких орбитах, влиянием атмосферы мы пренебрегать не можем. Атмосферное давление падает с высотой экспоненциально - на высоте 200 км оно составляет 10-12 мбар (на уровне моря атмосферное давление составляет 1013 мбар), а на высоте 900 км - уже только 10-42 мбар [6]. Тем не менее, даже такая разреженная атмосфера может приводить к изменению орбиты ИСЗ.

Сила сопротивления движущемуся в атмосфере телу определяется выражением [4]:

, (10)

где "с_x" - безразмерный коэффициент сопротивления, для верхней атмосферы равный 2-2,5; "S" - площадь максимального сечения спутника, перпендикулярного налетающему воздушному потоку; "v" - скорость ИСЗ, "ρ" - плотность атмосферы на высоте полёта ИСЗ. Торможение ИСЗ определяется его парусностью - чем больше площадь и меньше масса, тем больше торможение.

Для спутника, движущемся по круговой орбите, сопротивление атмосферы будет сказываться следующим образом: спутник будет медленно опускаться по спирали с постоянно увеличивающейся скоростью. Угол снижения спутника на круговой орбите можно оценить из выражения [1]:

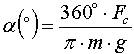, (11)

где "m" - масса ИСЗ, "g" - ускорение свободного падения. Снижение по спирали будет продолжаться до тех пор, пока спутник не опустится до высоты 160 км - ниже этой высоты сила сопротивления настолько велика, что спутник начинает резкое снижение и сгорит в атмосфере. На высоте 160 км период обращения равен примерно 88 минут - любой ИСЗ с меньшим периодом обречён.

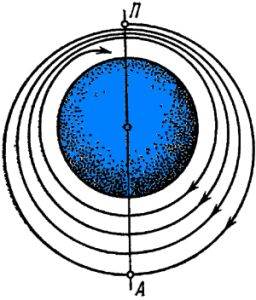Если орбита эллиптическая, то результат действия сопротивления атмосферы будет следующим: т.к. сопротивление сильно возрастает с высотой, то максимальное сопротивление ИСЗ будет испытывать в перигее, а минимальное - в апогее. Это слабо меняет высоту перигея, но уменьшает высоту апогея - в результате эллиптичность орбиты уменьшается и спутник начинает спуск по спирали. На рис. 10 показано снижение ИСЗ в случае эллиптической орбиты.

Рис. 10. Снижение спутника в атмосфере [4].

Оценить время жизни спутника можно из выражения (12) [1]:

, (12)

где e0 - начальный эксцентриситет орбиты, T0 - начальный период обращения, ΔT - суточное изменение периода. Тогда измение периода будет определятся выражением [1]:

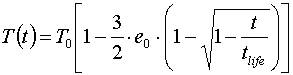, (13)

а изменение эксцентриситета [1]:

. (14)

Формулы (13) и (14) справедливы для значений e = 0,02-0,2. На атмосферное торможение сильно влияет время суток (в подсолнечной точке атмосфера подымается выше), а также активность Солнца.

Как видно, время жизни спутника определяется его эксцентриситетом и большой полуосью. В таблице ниже представлены времена жизни ИСЗ для разных значений перигея и апогея [5]:

Наше шестое важное положение - сопротивление атмосферы Земли вызывает уменьшение большой полуоси орбиты ИСЗ, в результате чего он по спирали спускается вниз. При достижении высоты около 160 км спутник сможет сделать всего пару оборотов и сгорит в атмосфере, войдя в резкий и необратимый спуск.

Давление света

Впервые идею о том, что свет производит давление на тела, высказал в 1619 г. И. Кеплер - для объяснения эффекта отклонения кометных хвостов от Солнца. Современная теория даёт значение давления следующим выражением (формула Максвелла-Бартоли) [3]:

p = E(1+η)/c, (15)

где "E" - мощность электромагнитного излучения, приходящаяся на единицу площади тела, "η" - коэффициент отражения тела, "c" - скорость света. Для абсолютно поглощающего тела вблизи Земли давление света равно 4,3 · 10^-6 Н/м². Для абсолютно отражающего тела эта величина в два раза больше. Световое давление становится ощутимым для лёгких спутников выше 500 км, т.к. ниже большее значение имеют колебания плотности атмосферы.

В заключении параграфа нужно отметить, что перечисленные факторы влияния на эволюцию орбиты спутника не составляют полный список. Например, на ИСЗ воздействуют своим притяжением Солнце и Луна, но это воздействие в 10000 раз слабее действия экваториального "горба" Земли, но его нужно учитывать для орбит с большим эксцентриситетом. Экваториальный "горб" также вызывает незначительные колебания плоскости орбиты ИСЗ при пересечении экваториальной плоскости. Наконец, неравномерность распределения масс под поверхностью Земли также сказывается на движении спутника.

Как видим, движение спутника не так просто, как может показаться на первый взгляд. В наше время расчёты эволюции орбиты значительно упростились с точки зрения затраты времени, т.к. современные компьютеры имеют огромную вычислительную мощность. Даже любители, используя специальные программы (см. далее), могут довольно точно расчитывать положение спутников на нужную им дату и время, причём на любой промежуток времени - в начале космической эры любители могли об этом только мечтать...

© BelAstro.Net, Lupus, 07.01.2011

Глава 2: Какие орбиты и ИСЗ бывают?

§ 1. Классификации орбит ИСЗ

п.1. Классификация орбит ИСЗ по наклонению

Экваториальные орбиты

Полярные орбиты

Солнечно-синхронные орбиты

п.2. Классификация орбит ИСЗ по величине большой полуоси

Низкоорбитальные ИСЗ (LEO)

Среднеорбитальные ИСЗ(MEO)

Геостационарные и геосинхронные орбиты ИСЗ

Высокоорбитальные ИСЗ (HEO)

п.3. Орбиты захоронения

§ 2. Классификации типов ИСЗ

Исследовательские спутники

ИСЗ дистанционного зондирования Земли

Космические корабли

Космические станции

Метеорологические спутники

Навигационные спутники

Разведывательные спутники

Спутники связи

Микроспутники

Глава 2: Какие орбиты и ИСЗ бывают?

В этой главе мы рассмотрим, какие спутники и их орбиты бывают, стараясь отразить лишь основные их виды.

За прошедшие более чем 50 лет с начала космической эры число ИСЗ в околоземном пространстве огромно - десятки тысяч объектов от более чем 100 метров в диаметре (МКС) до кусочков обшивки и т.п. размером 5-10 см. На рис. 1 можно увидеть распределение ИСЗ на полночь 17 января 2011 г. для более чем 14000 ИСЗ.

Рис. 1. Заселённость околоземного пространства ИСЗ. Слева - вид в экваториальной плоскости, справа - вид с северного полюса мира.

Чтобы не запутаться в этом многообразии "зверинца" ИСЗ и приводится нижеописанная классификация.

Приведённые классификации не претендуют на абсолютность - как известно, классифицировать можно что угодно по какому угодно признаку сколько угодно времени...

§ 1. Классификации орбит ИСЗ

В этом параграфе мы рассмотрим типы орбит ИСЗ. В Главе 1 мы видели, что все ИСЗ движутся по эллипсам, в одном из фокусов которых находится Земля. Следовательно, все типы орбит - эллиптичные. Основное деление орбит производят по величине наклонения "i" орбиты и по значению большой полуоси "a". Кроме того, можно выделить деление по величине эксцентриситета "e" - малоэллиптичные и высокоэллиптичные орбиты. Наглядное представление об изменении вида орбиты при различных значениях эксцентриситета дано на рис. 2.

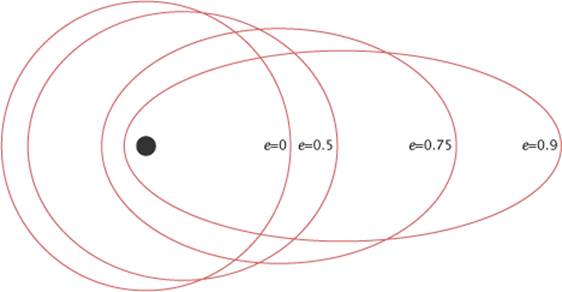
Рис. 2. Изменение вида эллиптической орбиты при разных значениях эксцентриситета "e". [1]

Итак, приступим к изучению типов орбит.

п.1. Классификация орбит ИСЗ по наклонению

В общем случае наклонение орбита ИСЗ лежит в диапазоне 0° < "i" < 90° (см. рис. 3). В зависимости от значение наклонения и высоты ИСЗ над поверхностью Земли, положение областей его видимости имеют различные границы широты, а в зависимости от высоты над поверхностью - и различный радиус этих областей. Чем больше наклонение, тем на более северных широтах может быть виден спутник, а чем он выше - тем шире область видимости. Таким образом, наклонение "i" и большая полуось "a" определяют перемешение по поверхности Земли полосы видимости ИСЗ и её ширину.

В общем случае параметры орбиты будут эволюционировать в зависимости от наклонения "i", большой полуоси "a" и эксцентриситета "e" ( см. §5 Главы 1).

Рис. 3. Общий случай орбиты спутника с наклонением 0° < "i" < 90°.

Экваториальные орбиты

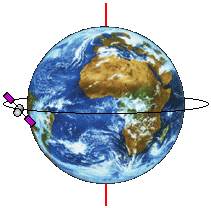Экваториальная орбита - крайний случай орбиты, когда наклонение "i" = 0° (см. рис. 4). В этом случае прецессия и поворот орбиты будут максимальны - до 10°/сутки и до 20°/сутки соответственно ( см. §5 Главы 1). Ширина полосы видимости спутника, которая расположена вдоль экватора, определяется его высотой над поверхностью Земли. Орбиты с малым наклонением "i" часто называют "около экваториальными".

Рис. 4. Экваториальная орбита.

Полярные орбиты

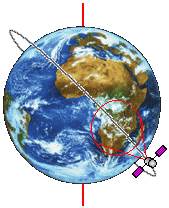
Полярная орбита - второй крайний случай орбиты, когда наклонение "i" = 90° (см. рис. 5). В этом случае прецессия орбиты отсутствует, а поворот орбиты происходит в сторону, обратную относительно вращения ИСЗ, и не превышает 5°/сутки ( см. §5 Главы 1). Подобный полярный ИСЗ последовательно проходит над всеми участками поверхности Земли. Ширина полосы видимости спутника определяется его высотой над поверхностью Земли, но спутник рано или поздно можно увидеть из любой точки. Орбиты с наклонением "i", близким к 90°, называют "приполярными".

Рис. 5. Полярная орбита.

Солнечно-синхронные орбиты

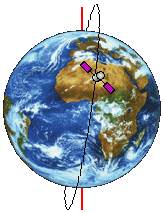
Рис. 6. Солнечно-синхронная орбита.

Солнечно-синхронная орбита (ССО) - особый вид орбиты, часто используемый спутникам, которые производят съёмку поверхности Земли. Представляет собой орбиту с такими параметрами, что спутник проходит над любой точкой земной поверхности приблизительно в одно и то же местное солнечное время [4]. Движение такого спутника синхронизировано с движением линии терминатора по поверхности Земли - за счёт этого спутник может лететь всегда над границей освещённой и неосвещённой солнцем территории, или всегда в освещённой области, или наоборот - всегда в ночной, причём условия освещённости при пролёте над одной и той же точкой Земли всегда одинаковые. Для достижения этого эффекта орбита должна прецессировать в сторону, обратную вращения Земли (т.е. на восток) на 360° в год, чтобы компенсировать вращение Земли вокруг Солнца. Такие условия соблюдаются только для определённого диапазона высот орбит и наклонений - как правило, это высоты 600-800 км и наклонение "i" должно быть порядка 98°, т.е. ИСЗ на солнечно-синхронных орбитах имеют обратное движение (см. рис. 6). При увеличении высоты полёта ИСЗ наклонение должно увеличиваться, из-за чего он не будет пролетать над полярными районами. Как правило, солнечно-синхронные орбиты близки к круговым, но могут быть и заметно эллиптичными. Из-за влияния возмущений спутник постепенно выходит из режима синхронизации, в связи с чем он периодически нуждается в коррекции своей орбиты при помощи двигателей.

п.2. Классификация орбит ИСЗ по величине большой полуоси

Вторая классификация - по величине большой полуоси, и точнее, по высоте над поверхностью Земли.

Низкоорбитальные ИСЗ (LEO)

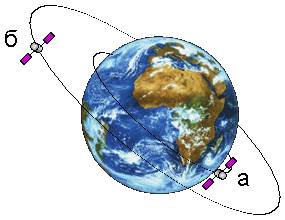Низкоорбитальными ИСЗ (НОС (рус.), рис. 7, а) обычно считаются спутники с высотами от 160 км до 2000 км над поверхностью Земли [5]. Такие орбиты (и спутники) в англоязычной литературе называют LEO (от англ. "Low Earth Orbit"). Орбиты LEO подвержены максимальным возмущениям со стороны гравитационного поля Земли и её верхней атмосферы. Угловая скорость спутников LEO максимальна - от 0,2°/с до 2,8°/с, периоды обращения от 87,6 минут до 127 минут.

Рис. 7. Низкоорбитальные ИСЗ (а) и среднеорбитальные ИСЗ (б).

Среднеорбитальные ИСЗ(MEO)

Среднеорбитальными ИСЗ (СОС (рус.), или "MEO" - от англ. "Medium Earth Orbit") обычно считаются спутники с высотами от 2000 км до 35786 км над поверхностью Земли [6] (рис. 7, б). Нижний предел определяется границей LEO, а верхний - орбитой геостационарных спутников (см. ниже). Эту зону в основном "заселяют" спутники навигации (ИСЗ "NAVSTAR" системы "GPS" летают на высоте 20200 км [7], ИСЗ системы "ГЛОНАСС" - на высоте 19100 км [8]) и связи, которые покрывают полюса Земли [6]. Период обращения - от 127 минут до 24 часов. Угловая скорость - единицы и доли угловой минуты в секунду.

Геостационарные и геосинхронные орбиты ИСЗ

Геостационарные ИСЗ (ГСС (рус.), или "GSO" - от англ. "Geosynchronous Orbit") считаются спутники, имеющие период обращение вокруг Земли, равный звёздным (сидерическим) суткам - 23ч 56м 4,09с. Если наклонение "i" орбиты нулевое, то такие орбиты называют геостационарными (см. рис. 8, а). Геостационарные ИСЗ летают на высоте 35786 км над поверхностью Земли [9]. Т.к. их период обращение совпадает с периодом обращения Земли вокруг своей оси, то такие ИСЗ "висят" в небе на одном месте (см. рис. 9). Если наклонение "i" не равно нулю, то такие ИСЗ называются геосинхронными (см. рис. 8, б). В реальности многие геостационарные спутники имеют небольшое наклонение и подвержены возмущениям со стороны Луны и Солнца, в связи с чем они описывают на небе фигуры в виде "восьмёрок", вытянутых в направлении север-юг.

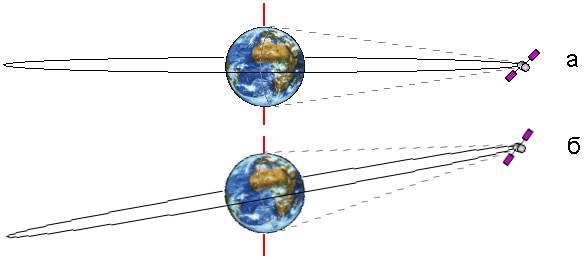Рис. 8. Геостационарный (а) и геосинхронный (б) ИСЗ.

Рис. 9. Снимок GEO, неподвижных на фоне вращения неба: 1 - Eutelsat W4 (NORAD №26369), 2 - Eutelsat W7 (NORAD №36101). Штрихи - треки звёзд. Снято 06.06.2010 с точки наблюдения RS на объектив "Юпитер 36Б" и DSLR-камеру "Canon 30D", сложено 12 кадров с выдержкой 30 с каждый. © В. Повалишев, В. Мечинский.

Если говорить о виде траектории ГСС, то он определяется значением наклонения наклонения "i", эксцентриситета "e" и аргумента перигея "Wp орбиты спутника (см. рис. 10). Если эксцентриситет и наклонение орбиты нулевые, то подспутниковая точка неподвижна и проецируется в конкретную точку поверхности Земли. При ненулевом эксцентриситете и нулевом наклонени ГСС "рисует" на поверхности отрезок, перемещаясь с востока на запад и обратно, смещаясь от нулевого положения не более чем на ΔLmax = 114.6°·e, т.е. при эксцентриситете e=0.01 смещение будет не более чем на 1.2°. Если наклонение ненулевое, а эксцентриситет нулевой, то ГСС "рисует" классические "восьмёрки" -- угловая высота 2Θ фигуры равна удвоенному значению наклонения i орбиты, максимальная ширина ΔLmax вычисляется по формуле 0.044·i2 (наклонение "i" задаётся в градусной мере). В самом общем случае при ненулевых "i" и "e" трек ГСС на поверхности Земли представляет собой "наклонённую восьмёрку", угловая высота 2Θ = i, максимальная ширина ΔLmax = 114.6°·e, причём "восьмёрка" получается только в том случае, если аргумент перигея "Wp" орбиты равен 0° и 180°, в остальных случаях получается более сложная фигура -- что-то среднее между овалом и "восьмёркой".

Рис. 10. Виды треков ГСС на поверхности Земли в зависимости от наклонения "i", эксцентриситета "e" и аргумента перигея "Wp" орбиты [20].

Ниже приводится материал по ГСС, подготовленный участником profi-s форума www.astronomy.ru/forum специально для нашего сайта.

В настоящее время на околоземных и геостационарных орбитах каталогизировано более 16000 космических объектов искусственного происхождения. Из них только около 6% являются "активными", т.е. функционирующими. ГСО является наиболее привлекательной, выгодной для решения многих научных, народнохозяйственных, военных, навигационных, коммерческих и иных задач. Около 80% активных, функционирующих ИСЗ дислоцируются на ГСО. В общем, это специальная орбита, на которой любой спутник будет висеть постоянно над одной точкой поверхности Земли.

Рис. 11. Анимация движения ГСС.

C точки зрения физики и небесной механики наличие ГСО можно объяснить двумя причинами:

Равнодействующая всех сил действующих на небесное тело (в нашем случае ГСС) равна нулю.

Угловая скорость вращения Земли и спутника равны.

При движении ИСЗ вокруг небесного тела на него действуют две основные силы: сила гравитации Fg и центробежная сила -Fc. На некотором расстоянии от Земли эти две силы уравновешивают друг друга: Fg = Fc. Когда равнодействующая всех сил, действующих на тело, равна нулю, то возникают условия устойчивого орбитального движения. Для вычисления этого расстояния можно воспользоваться простыми, известными со школы, методами классической механики. Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения Ньютона:

(*)

где m_ИСЗ -- масса спутника, M_⊕ -- масса Земли, G -- гравитационная постоянная, а r -- расстояние от спутника до центра Земли, или радиус орбиты. Величина центробежной силы равна:

. (**)

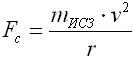Из уравнений (*) и (**) можно определить скорость движения спутника по круговой орбите:

.

При равенстве угловой скорости вращения Земли и спутника появляется область, обладающая уникальными свойствами. Такое равенство возможно только в плоскости небесного экватора. При вращении ИСЗ не в плоскости экватора, синхронность вращения Земли и ИСЗ обеспечить невозможно. Период обращения спутника вокруг Земли TИСЗ равен длине орбиты 2πr, делённой на скорость движения спутника v:

.

Когда орбитальный период TИСЗ будет равен периоду вращения Земли вокруг собственной оси (23ч 56м 04с), то спутник будет "висеть" над одним и тем же районом Земли, а круговая орбита, лежащая в этой области, называется геостационарной.

Геостационарная орбита ограничена в размерах и лежит в плоскости экватора Земли. Её радиус составляет 42164 км от центра Земли. Небесные координаты геостационарного спутника на геостационарной орбите теоретически будут постоянными. Основными причинами, искажающими кеплеровское движение пассивного геостационарного спутника, являются гравитационные возмущения (несферичность геопотенциала, лунно-солнечные возмущения), а для ГСС с большим отношением площади поверхности к массе -- еще и негравитационный (световое давление) фактор. В результате действия возмущающих сил появляется дрейф спутника, изменяющий период вращения вокруг Земли. Отличие периода вращения ГСС от теоретического приводит к тому, что средняя долгота ГСС меняется со временем: спутник медленно дрейфует с запада на восток, если его период обращения вокруг Земли меньше звездных суток, и с востока на запад в противном случае. Отличие эксцентриситета "e" от нуля также приводит к тому, что подспутниковая долгота ГСС меняется. Происходит незначительное изменение долготы (с периодом около 12ч и амплитудой, пропорциональной квадрату угла наклонения орбиты), и широты (с периодом 24ч и амплитудой, равной самому наклонению "i"). Вследствие этого подспутниковая точка описывает на поверхности Земли известную "восьмерку" (см. рис. 12).

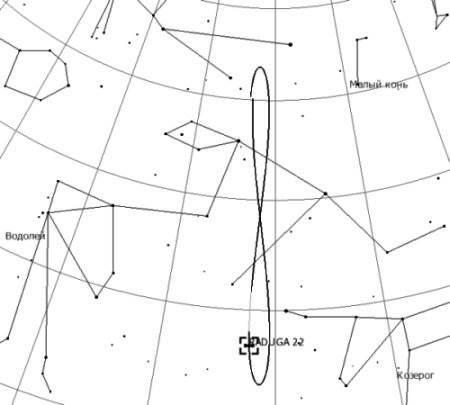
Рис. 12. Суточная траектория ГСС "RAGUGA 22" (SCN: 19596).

Резонансные влияния долготных членов в разложении геопотенциала Земли (неоднородность гравитационного поля Земли) приводит к тому, что на геостационарной орбите имеются два устойчивых положения (точки) равновесия с долготами 75° в.д. (точка либрации L1) и 255° в.д. (точка либрации L2). И два неустойчивых, отстоящих от устойчивых точек примерно на 90°. Эти точки либрации на ГСО не следует отождествлять с точками либрации в небесной механике при решении задачи "n" тел.

Геостационарная орбита вокруг Земли одна. Запуски спутников на ГСО начались с 1963 года. На начало 21 века более 40 стран планеты имеют свои геостационарные спутники. Ежегодно на ГСО запускается десятки спутников, орбита к тому же постепенно заполняется отработавшими спутниками. На ГСО постоянно происходят взрывы отработанных аппаратов и их ракет-носителей. Эти взрывы порождают десятки-сотни космических осколков, которые могут вывести из строя работающие аппараты. Засорение космическим мусором этой орбиты может привести к необратимым последствиям -- невозможности стабильного функционирования спутников. Космический мусор на ГСО, в отличие от близких околоземных орбит, может вращаться вокруг Земли тысячелетиями, угрожая столкновением с работающими КА. С конца 20 века проблема загрязнения ГСО стала общепланетарной, масштабной экологической проблемой.

Согласно международной конвенции по мирному использованию космического пространства при ООН, и требованиям международного радиочастного комитета (во избежании радиопомех на соседние ГСС), угловое расстояние между ГСС не должно быть менее 0.5°. Таким образом, теоретически количество ГСС, находящихся на безопасном расстоянии на ГСО, должно быть не более 720 штук. В последнее десятилетие это расстояние между ГСС не выдерживается. На 2011 год количество каталогизированных ГСС уже превысило более 1500. Сюда можно добавить более 600 высокоэллиптических объектов, периодически пересекающих ГСО и более 200 военных спутников, запущенных на ГСО в интересах Министерства обороны и разведки разных стран, которые не содержатся в публично доступном каталоге объединенного командования СПРН США и Канады (NORAD).

Наблюдения ГСО проводятся в оптическом и редко в радиодиапазоне. При использовании радиолокации со сверхдальней базой (РСДБ) координаты ГСС вычисляются точнее, чем при оптических наблюдениях. Но из-за больших энергетических затрат, и ввиду неэффективности, наблюдения ГСО в радиодиапазоне проводятся редко. Хотя для решения таких статистических задач околоземного пространства, как обнаружение облаков фрагментов мелкого космического мусора размеров от 5-50 см, радиолокационный метод эффективней, чем наблюдения в оптическими диапазоне. При использовании лазерной локации наклонная дальность до объекта определяется с ошибкой несколько см. Но для эффективной работы радиолокатора и лазерной установки необходимы высокоточные координаты спутника на небесной сфере. Такие координаты можно получить только с помощью наблюдения на оптических телескопах, расположенных на поверхности Земли.

Оптические телескопы с полем зрения в несколько градусов, изготовленные для задач мониторинга ГСО, имеют поле зрения в десятки и более раз больше, чем ширина диаграммы направленности радиотелескопов. Фотометрические наблюдения в оптическом диапазоне позволяют по видимому блеску оценить размеры аппарата, а по зависимости блеска от времени и угла освещения Солнцем судить о его форме и способе ориентации. Поэтому оптические инструменты являются наиболее эффективными для задач контроля ГСО. Недостатком оптических наблюдений является их зависимость от состояния неба, т.е они не всепогодны.

К геостационарным спутникам принято относить спутники с периодами от 22ч до 26ч, эксцентриситетами "e" не более 0.3 и наклонами плоскости орбиты к плоскости экватора "i" до 15°, но в некоторых источниках можно встретить и более подробную классификацию, и более жесткие границы.

Классификацию ГСС можно провести по нескольким признакам: по степени "активности", по функциональному назначению, по орбитальному движению. По первому признаку все ГСС можно разделить на 2 класса:

"Активные" -- имеющие энергетический ресурс и управляемые по командам с Земли.

"Пассивные" -- неуправляемые с Земли искусственные объекты, выработавшие ракетное топливо и перешедшие в категорию космического мусора. Это ракеты-носители, фрагменты ступеней, выводившие спутники на орбиту, многочисленные детали, сопутствующие запуску, осколки спутников, образовавшиеся после взрывов аппарата на орбите, или столкновений между собой, либо с метеороидными телами.

По функциональному назначению:

Научные.

Геодезические.

Метеорологические.

Навигационные.

Военного назначения, которые делятся на несколько подклассов (оптическая, радиотехническая, радиолокационная разведка, предупреждение ракетно-ядерного нападения -- СПРН).

Спутники радио-телесвязи (в том числе коммерческие).

Инженерные.

Функционально многие спутники можно отнести к спутникам двойного назначения, которые составляют 70%-80% от общего числа активных ИСЗ. Это навигационные, метеорологические, спутники связи, дистанционного зондирования Земли (ДЗЗ).

Классификация ГСС по орбитальному движению согласно А.С. Сочилиной, Р.И. Киладзе относительно точек либрации L1, L2 [18-19]:

Класс С – активные, корректируемые ГСС (38% от общего числа ГСС). Этот класс объектов удерживаются на одной долготе с помощью коррекции орбиты. В зависимости от типа коррекции, орбитальных параметров и долготы активные геостационары иногда разделяют на подклассы. В промежутках времени между коррекциями эти объекты обычно ведут себя как либрационные. "Время жизни" активных ГСС -- 10-15 лет, далее они или становится либрационными или пополняет класс дрейфующих объектов.

Класс L1 –- ГСС, движущиеся в режиме либрации относительно устойчивой точки с долготой 75° в.д. (10%).

Класс L2 -– то же для точки с долготой 255° в.д. (4%).

Класс L3 -– небольшое количество пассивных объектов с дрейфом, близким к критическому, они способны менять точку либрации или режим движения (менее 1%).

Класс D1 -– ГСС с отрицательным дрейфом, меньшим -2.5° в сутки (22%).

Класс D2 -– дрейфующие ГСС с дрейфом от -2.5° до +2.5° в сутки (16%). Примерно 1/3 их постоянно движется с запада на восток, а 2/3 - с востока на запад.

Класс D3 -– ГСС с положительным дрейфом, большим +2.5° в сутки (10%).

Высокоорбитальные ИСЗ (HEO)

Высокоорбитальными ИСЗ (ВОС (рус.), или "HEO" - от англ. "High Earth Orbit") считаются спутники, достигающие высот более 35786 км над поверхностью Земли [9], т.е. залетающие выше геостационарных спутников (см. рис. 10). Орбиты могут иметь значительный эксцентриситет (например, спутники серии "Меридиан", "Молния") - в этом случае они называются высокоэллиптичными (ВЭС), так и быть почти круговыми (пример - ИСЗ "Vela" (те самые ИСЗ, на которых в конце 60-х гг. ХХ в. были открыты гамма-всплески)).

Рис. 13. Орбита ВЭС.

Рис. 14. Анимация движения НЕО.

п.3. Орбиты захоронения

Орбиты захоронения - отдельный класс орбит ИСЗ, специально предназначенный для увода на них спутников, вышедших из строя для уменьшения вероятности столкновения с работающими спутниками и для освобождения места новым ИСЗ. Для ГСС орбитой захоронения считается орбита, на 200 км выше самой орбиты ГСС (см. рис. 12) [11].

Рис. 15. Орбита захоронения ГСС.

Для каждого ГСС спутника орбита захоронения расчитывается отдельно, причём минимальный перигей ΔH равен:

, (1)

где "C_R" - коэффициент давления света, "S" - площадь ИСЗ, "m" - его масса.

Низкоорбитальные спутники с ядерными реакторами на борту [12] имеют высоту орбиты захоронения порядка 1000 км, куда переводится активная зона ядерного реактора после окончания ее работы [11].

§ 2. Классификации типов ИСЗ

Исследовательские спутники

Это спутники, предназначенные для исследования планет, галактик и других космических объектов.

Примером таких аппаратов являются орбитальные телескопы ("AGILE" (NORAD №31135), Италия, γ-телескоп; "AKARI" (NORAD №28939), Япония, ИК-телескоп; "Chandra" (NORAD №25867), США, рентгеновская обсерватория; "COROT" (NORAD №29678), ЕС, телескоп видимого диапазона длин волн; "Herschel Space Observatory" (ранее "FIRST", NORAD №34937), ЕС, ИК-телескоп; "Fermi Gamma-ray Space Telescope" (ранее "GLAST", NORAD №33053), США, ЕС, γ-телескоп; "Hubble Space Telescope" (NORAD №20580), США, ЕС, телескоп УФ, ИК и видимого диапазона и т.д.).

ИСЗ дистанционного зондирования Земли

Эти спутники осуществляют дистанционное зондирование Земли (ДЗЗ) в различных спектральных диапазонах. Диапазон длин волн, принимаемых съёмочной аппаратурой, составляет от УФ до ИК и радиоволн [13]. Спутники служат для слежением за состоянием флоры и фауны, климата, морских и воздушных течений течений, разведки полезных ископаемых и т.д. Примером таких аппаратов мгут служить спутники серии "Landsat", ИСЗ "AQUA", "AURA" и т.д. Обычно подобные ИСЗ запускают на солнечно-синхронные орбиты.

Космические корабли

Пилотируемые космические аппараты. Примерами являются российские корабли серии "Союз" и американские челноки "Space shuttle".

Космические станции

Долговременные космические корабли. В настоящее время на орбите присутствует только один такой объект - "Международная космическая станция" (МКС) [14].

Метеорологические спутники

Это спутники, предназначенные для передачи данных в целях предсказания погоды, а также для наблюдения климата Земли.

Навигационные спутники

Это спутники, обеспечивающие решение задачи навигации на Земле. В настоящее время глобальными системами навигации является GPS и ГЛОНАСС.

Разведывательные спутники

Это спутник для наблюдения Земли или спутник связи, применяющийся для разведки [16].

Спутники связи

Искусственный спутник Земли, специализированный для ретрансляции радиосигнала между точками на поверхности земли, не имеющими прямой видимости [17].

Микроспутники

Это малые космические аппараты (массой менее 500 кг), разрабатываемые университетами, частными компаниями и даже любителями. На данном этапе стали весьма востребованными по причине своей относительно низкой стоимости и доступности. Многие университеты США, Европы, Японии запускают свои микроспутники, которые выполняют задачи ДЗЗ, связи между радиолюбителями, отработки новых технологий.

Типы орбит движения спутников.

Какие же типы орбит движения спутников существуют?

Всего существует три типа орбит движения спутников, названия которых определяются нахождением спутников в зависимости от угла между плоскостями орбиты и экватора Земли, а именно, - полярная орбита, наклонная орбита и экваториальная орбита (геостационарная орбита).

Полярная орбита – это орбита, имеющая наклонение i орбиты к плоскости экватора в 90°. Полярная орбита, также как и наклонная орбита (которая смещена под углом между полярной и экваториальной орбитами), имеет существенный недостаток: так как спутник движется по этим орбитам, то для того, чтобы отслеживать положение спутника антенну нужно обязательно подстраивать для получения спутникового сигнала., а для это, в свою очередь, требуется специальное оборудование, которое стоит немалых денег: их очень сложно устанавливать и обслуживать.

Экваториальная орбита (или геостационарная орбита) находится в экваториальной плоскости нашей планеты. Двигаясь по ней, спутник делает оборот ровно за то время, за которое Земля обращается вокруг своей оси. Поэтому он кажется неподвижным и как-будто находится постоянно в одной точке. Это очень удобно для ретрансляции сигналов, так как не нужно регулировать положение рефлекторов антенн, направляя их на уходящий спутник.

Экваториальная орбита (или геостационарная орбита) – имеет высоту над поверхностью Земли 35876 км, радиус 442241 км, длину 265409 км. Именно экваториальную орбиту используют большинство спутников коммерческого назначения. Экваториальная орбита (или геостационарная орбита) помимо положительных имеет и отрицательные характеристики: - невозможно передавать сигнал на приполярные районы Земли, так как угол местности очень мал; - из-за того, что несколько спутников на одной орбите могут находиться только на небольшом расстоянии друг от друга, то происходит перенасыщение геостационарной орбиты.

Р. А. Ахмеджанов