ТЕОРИЯ СОУДАРЕНИЙ

В 1918г. Льюис предположил, что для протекания реакции А + В = АВ должны столкнуться две молекулы А и В. Поэтому, зная число столкновений, можно, казалось бы, рассчитать скорость химической реакции. Однако если сравнить расчетное число соударяющихся молекул с числом реагирующих молекул, которое определяется экспериментально, то обнаруживаются два противоречия. Во-первых, число соударений примерно в 10¹⁷ раз больше числа реагирующих молекул, т.е. из каждых 10¹⁷ соударений только одно соударение является эффективным в осуществлении реакции. Во-вторых, в то время как при повышении температуры на 10⁰С число бинарных столкновений увеличивается примерно на 2%, скорость химической реакции возрастает на 200-300%.

Эти противоречия были разрешены при допущении, что реакция происходила только в том случае, если соударяющиеся молекулы обладали некоторой избыточной энергией; все остальные соударения неэффективны и не приводят к химической реакции, т.е. скорость реакции равна общему числу соударений, умноженному на долю эффективных соударений. Это допущение опиралось на изучение: 1) распределения скоростей реагирующих молекул и 2) влияния температуры.

1. Закон распределения скоростей. Все молекулы газа движутся с различными скоростями из-за частых соударений. Между молекулами постепенно происходит взаимообмен количеством движения и, следовательно, их скорости изменяются: одни молекулы увеличивают свою скорость, другие – уменьшают. Математический закон, которому подчиняется распределение скоростей и энергий, был найден Максвеллом и Больцманом в 1860г. Согласно этому закону, доля DN/N молекул, обладающих большими скоростями, чем средняя скорость и , или кинетической энергией, превышающей величину ½ mи² , составляет:

( )

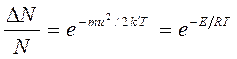где k’ – константа Больцмана; u - средняя квадратичная скорость, см/с.

В дифференциальной форме это уравнение имеет вид:

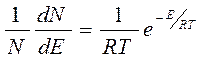, (45)

где R - универсальная газовая постоянная, эрг; Т - температура газа, К.

На рисунке 3 представлен график, построенный по уравнению (45). Доля молекул, энергия которых лежит в пределах определенного интервала, изображается площадью столбика, ограниченного кривой и соответствующими ординатами.

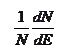Рисунок 3. Распределение энергии по Максвеллу-Больцману.

В результате соударений всегда имеется несколько молекул с энергиями, намного превосходящими среднее значение. Таким образом, возможны столкновения между молекулами, имеющими высокую энергию активации, необходимую для реакции, но число таких соударений будет составлять очень небольшую долю от общего числа столкновений, происходящих в газе. Это объясняет тот факт, что лишь небольшая часть соударений приводит к реакции.

2. Влияние температуры на распределение скорости (см. Рис. 5.). С ростом температуры наблюдается смещение максимума в сторону более высокой скорости; происходит резкое увеличение числа молекул, имеющих скорости намного выше средней [при скорости w имеется число (доля) молекул n₁, при температуре Т₁, которое увеличивается до n₂ при температуре Т₂, T₂ > T₁]. Общее число молекул, имеющих скорости, равные или большие определенного значения w, определяются площадью под кривой. Но именно небольшая доля молекул n₁ и n₂ при температурах Т₁ и Т₂ в конце кривых распределения, обладающих максимальными энергиями и скоростями в сечениях и будет определять эффективную долю столкновений, приводящих к их взаимодействию.

Экспоненциальный фактор в уравнении Максвелла учитывает изменение формы кривой при повышении температуры. Если , где М – молекулярный вес, то член будет представлять собой кинетическую энергию 1 моля молекул, каждая из которых имеет одну и ту же скорость u . Член exp(-E/RT) называется фактором Больцмана. Этот фактор заметно увеличивается с увеличением температуры. Хотя общее число столкновений незначительно изменяется с ростом температуры, доля эффективных столкновений сильно повышается. Таким образом, отмеченное влияние температуры на скорость реакции может быть объяснено тем, что в газах (или растворах) имеются молекулы со всеми значениями скоростей и кинетических энергий. Число молекул с энергией, равной или большей, определенного значения Е, составляет приблизительно exp(-E/RT) часть от общего числа молекул. Так, например, повышение абсолютной температуры газа вдвое (например от 1000 К до 2000 К) приводит к увеличению средней кинетической энергии молекул в 2 раза, но доля молекул, обладающих энергией свыше 80 кДж/моль возрастает в 150 раз.