Коэффициент передачи одноконтурной входной цепи.
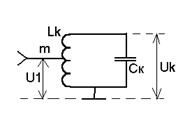 Про входные цепи (В.Ц.): одноконтурная В.Ц. является простейшей, однако в данном случае все вопросы согласования полосового фильтра В.Ц. с источником сигнала и с нагрузкой решается также как и в случае с более сложным полосовым фильтром.
Про входные цепи (В.Ц.): одноконтурная В.Ц. является простейшей, однако в данном случае все вопросы согласования полосового фильтра В.Ц. с источником сигнала и с нагрузкой решается также как и в случае с более сложным полосовым фильтром.
1) автотрансформаторная связь (неполное включение индуктивности)
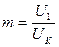 - коэффициент включения в контур внешней цепи.
- коэффициент включения в контур внешней цепи.
Достоинство: частотная независимость характеристик связи
Недостаток: эта связь нерегулируемая
2) трансформаторная связь
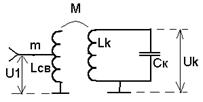
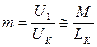
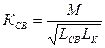 , КСВ – коэффициент связи.
, КСВ – коэффициент связи.
В теории КСВ ≤ 1 На практике КСВ ≤ 0,5 – 0,6
КСВ – характеризует конструктивное исполнение трансформаторной связи.
Достоинство: регулировка коэффициента включения
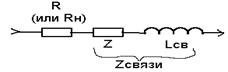
Недостаток: частотная зависимость характеристик внешней цепи. Внешняя цепь своему выходному сопротивлению подключает еще и индуктивность LСВ и сопротивление потерь.
Передача сигнала от контура к внешней цепи определяется внутренним сопротивлением источника сигнала (или сопротивлением нагрузки) и индуктивностью катушки связи.
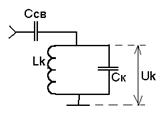 3) внешне емкостная связь – необходима для ослабления влияния реактивности на настройку контура. Подключение контура через малую ёмкость. Она обеспечивает снижение влияния реактивности антенны на настройку контура.
3) внешне емкостная связь – необходима для ослабления влияния реактивности на настройку контура. Подключение контура через малую ёмкость. Она обеспечивает снижение влияния реактивности антенны на настройку контура.
Достоинство: низкая стоимость
Недостаток: частотная зависимость
коэффициента передачи 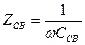
4) внутри емкостная связь
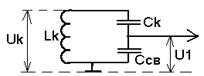 В данном случае внешняя цепь подключена к контуру через внутри емкостную связь.
В данном случае внешняя цепь подключена к контуру через внутри емкостную связь.
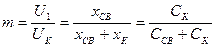
Обычно m <<1 => 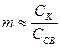 ,т.к. ССВ >>CK
,т.к. ССВ >>CK
Достоинство: реализуется проще чем автотрансформаторная связь
Недостаток: частотная зависимость коэффициента передачи.
5) комбинированная связь
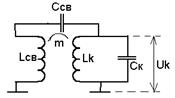
Достоинство: более стабильный коэффициент передачи при перестройке входной цепи в диапазоне частот.
Недостаток: сложность настройки
Коэффициент передачи входной цепи
Рассмотрим коэффициент передачи входной цепи, когда источник сигнала и нагрузка имеют автотрансформаторную связь с контуром. Полученные результаты потом распространим на все остальные варианты связи.
Z1 = ZA + ZСВ
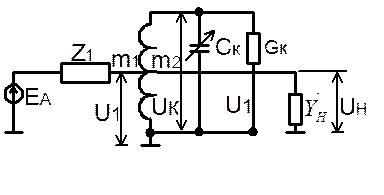 GK – собственная проводимость контура
GK – собственная проводимость контура
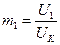 ;
; 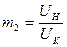 ; КВЦ =
; КВЦ = 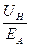 = ?
= ?
Заменим неполное включение внешних цепей некоторым эквивалентом цепей.
I’С ЭК = IС ЭК ∙ m1 Y’1 = Y1∙ (m1)2
 IС ЭК =
IС ЭК = 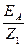 Y1 =
Y1 = 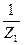 Y’Н = YН∙ (m1)2
Y’Н = YН∙ (m1)2
Y = G + jB Суммируем отдельно активные компоненты комплексных проводимостей получая в итоге эквивалентную активную проводимость контура и отдельную реактивность. Результат суммирования учитываем путём изменения параметров контура СК и LK.

GЭК = GК +G’Н + G’1 = GК +(m2)2GН + (m1)2G1
Найдём напряжение на контуре:
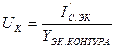 YЭК = jωC +
YЭК = jωC + 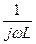 +GЭК
+GЭК
Преобразуем YЭК чтобы выявить её зависимость от обобщённой расстройки контура.
YЭК = GЭК [1+ 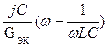 ] учтём, что
] учтём, что 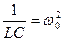 , где ω – резонансная частота контура
, где ω – резонансная частота контура
YЭК = GЭК [1+ 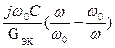 ] учтём, что
] учтём, что 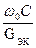 =QЭК–эквивалентная добротность контура
=QЭК–эквивалентная добротность контура
YЭК = GЭК [1+ 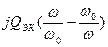 ] = GЭК (1+jξ)
] = GЭК (1+jξ) 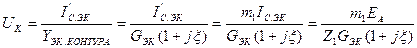
UH =m2UK КВЦ = UH / EA = 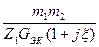
Резонансное значение коэффициента передачи: К0 ВЦ = 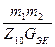
Используя выражения m1 и m2, а так же Z1 для конкретной схемы включения контура можно из данного выражения коэффициента передачи получить коэффициент передачи для любой из схем подключения контура во входную цепь.
Для обеспечения максимальной чувствительности приёмника необходимо обеспечить максимум коэффициента передачи входной цепи. Рассмотрим возможность получения максимума при изменении коэффициентов включения m1 и m2. Необходимо найти оптимальное значение m1 и m2, при котором достигается максимум коэффициента передачи. Чтобы при оптимизации учесть изменение фильтрующей способности контура необходимо при поиске оптимальных значений m1 и m2 наложить ограничения на допустимую степень снижения добротности контура.
D = 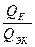 , где QК – собственная добротность контура QЭК - добротность контура с подключенными цепями.
, где QК – собственная добротность контура QЭК - добротность контура с подключенными цепями.
D = 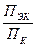 ПЭК – полоса пропускания D =
ПЭК – полоса пропускания D = 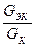 ; К0 =
; К0 = 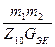 ; GЭК = GК +(m2)2GН + (m1)2G1 m1 =
; GЭК = GК +(m2)2GН + (m1)2G1 m1 = 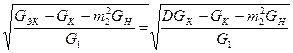
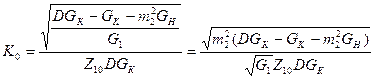 ;
;
Найдём максимум функции y:
у = 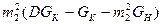
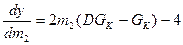
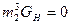
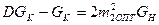 →
→ 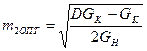
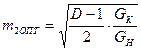
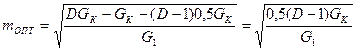
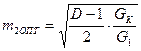
Определим значения коэффициента передачи при оптимальных значениях коэффициента включения: К0 ВЦ = 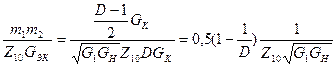
Рассмотрим случай когда сопротивление антенны является чисто активным и отсутствует элемент связи между антенной и полосовым фильтром
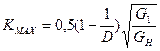 Z10 = RA + ZСВ при ZСВ =0 Z10 = RA =
Z10 = RA + ZСВ при ZСВ =0 Z10 = RA = 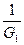 ,где G1 - проводимость источника сигнала
,где G1 - проводимость источника сигнала
Если собственные потери в контуре отсутствуют, то имеет место верхняя граница коэффициента передачи входной цепи. Выше данного значения получить коэффициент передачи нельзя. 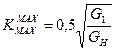
Дата добавления: 2014-12-24; просмотров: 3932;
