Структурна класифікація плоских механізмів. Основний принцип створення механізмів

У сучасному машинобудуванні особливо поширені плоскі механізми, ланки яких входять в кінематичні пари IV i V класів. Розглянемо принципи їх структурної класифікації.

Структурна класифікація Ассура-Артоболевського є однією з найраціональніших класифікацій плоских механізмів. Перевагою цієї класифікації є те, що вона пов’язується з методами кінематичного та динамічного дослідження механізмів. Класифікація універсальна, охоплює усі існуючі і можливі нові механізми; визначає напрямки дослідження механізмів, вказує шляхи утворення нових механізмів.

В основі її лежить основний принцип створення механізмів, сформульований в 1914 р. Л.В. Ассуром. Ним був запропонований метод створення механізмів шляхом послідовного нашарування кінематичних ланцюгів, що мають певні структурні властивості: будь-який механізм може бути створений шляхом послідовного приєднання до однієї (чи декількох) початкових ланок та стояка кінематичних ланцюгів з нульовим ступенем вільності. Такі кінематичні ланцюги з нульовим ступенем вільності називають структурними групами або групами Ассура, а початкову ланку та стояк - механізмом І класу.

Таким чином, будь - який механізм можна отримати послідовним приєднанням до механізму І класу (одного чи декількох) груп Ассура.

Структурною групою Ассура називається кінематичний ланцюг, приєднання якого до механізму не змінює ступеня вільності механізму.

Існують інші визначення, наприклад: кінематичний ланцюг, число ступенів вільності якого відносно елементів його зовнішніх кінематичних пар дорівнює нулю, називають групою Ассура , якщо з нього не можна виділити простіші кінематичні ланцюги, що задовільняють цій умові. Отже, основною ознакою групи Ассура є рівність нулю її ступеня вільності, W_Гр = 0.

Сукупність стояка та початкової ланки, що утворюють кінематичну пару V класу, умовно називають механізмом І класу (найпростішим, початковим механізмом); число механізмів І класу дорівнює числу ступенів вільності механізму.

Отже, механізми І класу являють собою найпростіші дволанкові механізми, що складаються з рухомої ланки та стояка, що з’єднані між собою або однією обертовою, або - поступальною кінематичною парою V класу (рис. 1.9); ступінь вільності механізму І класу рівний одиниці. Механізми І класу, що мають обертову пару, досить поширені в техніці. Це механізми таких машин як електродвигуни, генератори, турбіни, вентилятори, відцентрові помпи і т.ін..

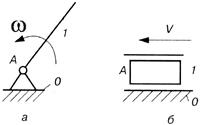
Рис. 1.9

Усі складніші можуть бути отримані шляхом приєднання до механізмів І класу додаткових кінематичних ланцюгів - структурних груп Ассура.

Очевидно, щоб створити новий механізм з одним ступенем вільності, W =1 (з іншими властивостями), до механізму І класу треба приєднати лише такі кінематичні ланцюги, які мають W=0, тобто групи Ассура.

При розгляді питань класифікації механізмів зручно обмежитися розглядом механізмів, у яких всі вищі пари IV класу попередньо замінені відповідними кінематичними ланцюгами, що утворені лише кінематичними парами V класу, p₄=0. Тоді, для структурних груп Ассура, справедлива рівність

W_Гр=3n-2p₅=0. (1.4 )

З (1.4) дістанемо співвідношення p₅= 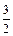n. Оскільки кількість кінематичних пар завжди ціле число, то кількість ланок в групі Ассура завжди парна; умові (1.4) відповідають лише такі співвідношення ланок і кінематичних пар, що входять у групу Ассура:

Таблиця 1.1

Зауважимо, що групи Ассура можуть мати лише парне число ланок, бути дво-, чотири-, шестиланковими і т.ін. Задаючись співвідношеннями ланок і кінематичних пар (табл. 1.1), можна дістати різні групи Ассура. Усі одержані таким чином групи Ассура поділено на класи: II, III, IV і т.д. У свою чергу, приєднуючи до механізму (чи механізмів) I класу групи Ассура різних класів, можна отримати найрізноманітніші механізми, відповідно механізми II, III, IV і т.д. класів.

Відзначимо що поділ груп за класами обумовлено методами кінематичного і силового аналізів, що властиві групам кожного класу.

Отже, найпростіша група Ассура складається з двох ланок і трьох кінематичних пар V класу - група Ассура ІІ класу ІІ порядку або двоповодкова група. Оскільки пари V класу в плоских механізмах можуть бути обертовими та поступальними, то в залежності від співвідношення їх числа та розташування можливі 5 видів (модифікацій) такої групи. На рис. 1.10, а зображено групи Ассура ІІ класу ІІ порядку І, ІІ, ІІІ, IV, V видів; штриховими лінями показані ланки (поводки), до яких приєднуються дані структурні групи; це можуть бути рухома ланка або стояк механізму І класу, або ж ланки інших, вже приєднаних груп Ассура, при цьому не можна приєднувати структурну групу до однієї ланки.

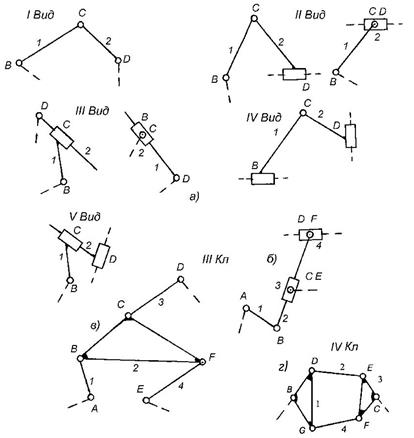
Рис. 1.10

Зазначимо, що, приєднуючи до механізму І класу групу Ассура ІІ класу ІІ порядку І виду, дістанемо шарнірний чотириланковик, рис. 1.3, а ; - ІІ виду – кривошипно-повзунний механізм, рис. 1.1; - ІІІ виду - кулісний механізм, рис. 1.3, в. Механізми, до складу яких входять групи Ассура не вище другого класу - це механізми ІІ класу.

Наступна, більш складна група Ассура, складається з чотирьох ланок і шести кінематичних пар - група ІІІ класу ІІІ порядку або триповодкова група. Характерною особливістю цієї групи є наявність ланки, що входить в три кінематичні пари і утворює жорсткий трикутник; таку ланку називають базисною. Найпростіша група ІІІ класу, з одними обертовими парами, зображена на рис. 1.10, в. В частинному випадку базисна ланка може бути прямолінійною, а деякі кінематичні пари - поступальними (рис. 1.10, б). Механізми, до складу яких входять групи Ассура не вище третього класу - механізми ІІІ класу.

Другий можливий кінематичний ланцюг, що складається з чотирьох ланок і шести пар (рис. 1.10, г) – група ІV класу ІІ порядку. Особливістю цієї групи є наявність рухомого чотиристороннього замкненого контуру. Очевидно, можливо отримати різні модифікації цих груп, якщо обертові пари комбінувати з поступальними.

Більш складні групи V і вищих класів використовуються обмежено і тут не розглядаються.

Таким чином групи Ассура діляться на класи і порядки. Клас групи Ассура визначається найвищим класом контура, що входить до її складу (за І.І. Артоболевским, клас структурної групи Ассура визначається числом кінематичних пар, що утворюють найбільш складний замкнутий контур). Основою структурної групи є замкнутий контур. Клас контура визначається кількістю кінематичних пар, у які входять ланки, що його утворюють. Механізму І класу присвоюють І клас контура (контур виродився у точку; є лише одна кінематична пара); ланка з двома парами – ІІ клас (також частковий випадок замкнутого контура – контур виродився у пряму); жорстка ланка з трьома парами – ІІІ клас (рис. 1.11, в – трикутник); контур з чотирма парами – ІV клас і т.ін.

Порядок групи Ассура визначається кількістю вільних (зовнішніх) елементів кінематичних пар (поводків), якими група Ассура приєднується до існуючого механізму.

Вид групи Ассура для груп ІІІ та вищих класів не визначається.

Клас механізму в цілому визначається найвищим класом групи, яка входить до його складу. Зазначимо, визначаючи клас механізму, потрібно вказати, яка з ланок є початковою, оскільки в залежності від її вибору може змінюватися клас механізму.

Структурний аналіз механізму належить проводити шляхом розбивки його на структурні групи Ассура та механізми І класу у послідовності, зворотній до утворення механізму.