АЛГОРИТМ ОБУЧЕНИЯ ПЕРСЕПТРОНА

Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход. Допустим, что входные образы нанесены на демонстрационные карты. Каждая карта разбита на квадраты и от каждого квадрата на персептрон подается вход. Если в квадрате имеется линия, то от него подается единица, в противном случае – ноль. Множество квадратов на карте задает, таким образом, множество нулей и единиц, которое и подается на входы персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.

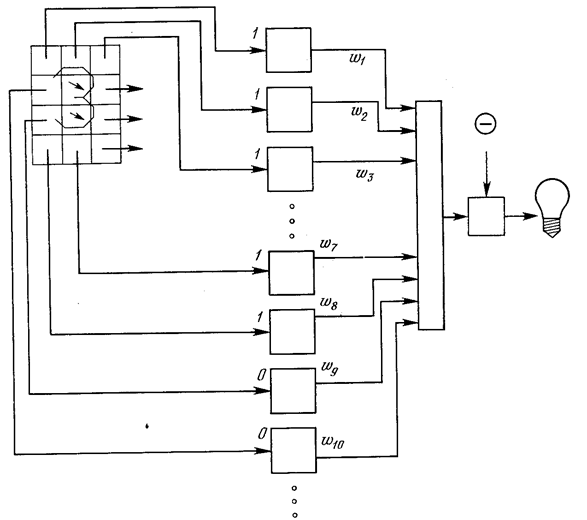
Рис. 1.10. Персептронная система распознавания изображений

На рис. 2.10 показана такая персептронная конфигурация. Допустим, что вектор Х является образом распознаваемой демонстрационной карты. Каждая компонента (квадрат) Х – (x₁, x₂, …, x_n) – умножается на соответствующую компоненту вектора весов W – (w₁, w₂, ..., w_n). Эти произведения суммируются. Если сумма превышает порог Θ, то выход нейрона Y равен единице (индикатор зажигается), в противном случае он – ноль. Как мы видели в гл. 1, эта операция компактно записывается в векторной форме как Y =XW, а после нее следует пороговая операция.

Для обучения сети образ Х подается на вход и вычисляется выход Y. Если Y правилен, то ничего не меняется. Однако если выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируются, чтобы уменьшить ошибку.

Чтобы увидеть, как это осуществляется, допустим, что демонстрационная карта с цифрой 3 подана на вход и выход Y равен 1 (показывая нечетность). Так как это правильный ответ, то веса не изменяются. Если, однако, на вход подается карта с номером 4 и выход Y равен единице (нечетный), то веса, присоединенные к единичным входам, должны быть уменьшены, так как они стремятся дать неверный результат. Аналогично, если карта с номером 3 дает нулевой выход, то веса, присоединенные к единичным входам, должны быть увеличены, чтобы скорректировать ошибку.

Этот метод обучения может быть подытожен следующим образом:

1. Подать входной образ и вычислить Y.

2 а. Если выход правильный, то перейти на шаг 1;

б. Если выход неправильный и равен нулю, то добавить все входы к соответствующим им весам; или

в. Если выход неправильный и равен единице, то вычесть каждый вход из соответствующего ему веса.

3. Перейти на шаг 1.

За конечное число шагов сеть научится разделять карты на четные и нечетные при условии, что множество цифр линейно разделимо. Это значит, что для всех нечетных карт выход будет больше порога, а для всех четных – меньше. Отметим, что это обучение глобально, т. е. сеть обучается на всем множестве карт. Возникает вопрос о том, как это множество должно предъявляться, чтобы минимизировать время обучения. Должны ли элементы множества предъявляться- последовательно друг за другом или карты следует выбирать случайно? Несложная теория служит здесь путеводителем.