Доверительный интервал и доверительная вероятность
| |
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.
График нормального закона распределения Гаусса представлен на рис.1. Уравнение кривой имеет вид

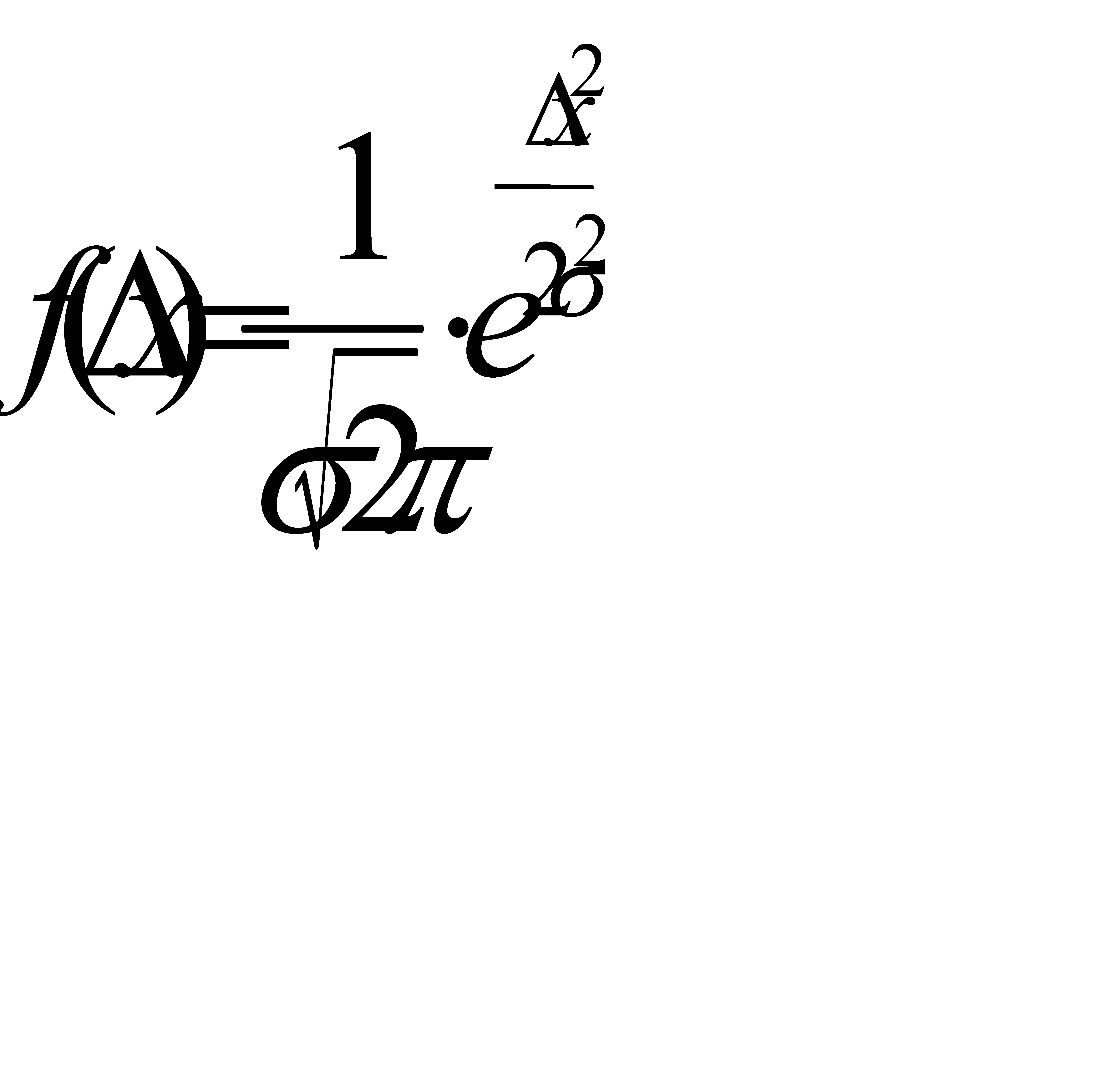 , (2)
, (2)
где 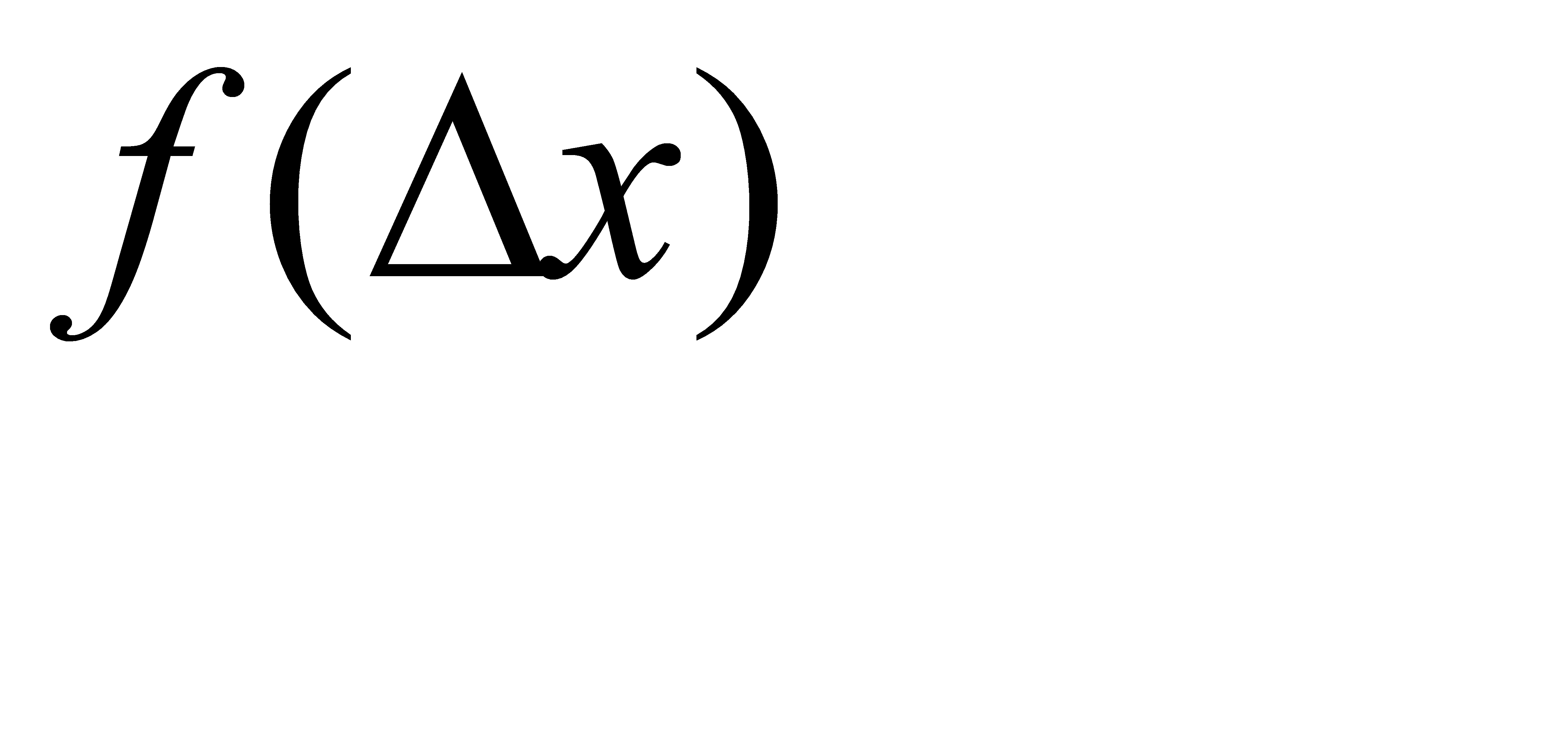 - функция распределения случайных ошибок (погрешностей), характеризующая вероятность появления ошибки
- функция распределения случайных ошибок (погрешностей), характеризующая вероятность появления ошибки 
 , σ – средняя квадратичная ошибка.
, σ – средняя квадратичная ошибка.
Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 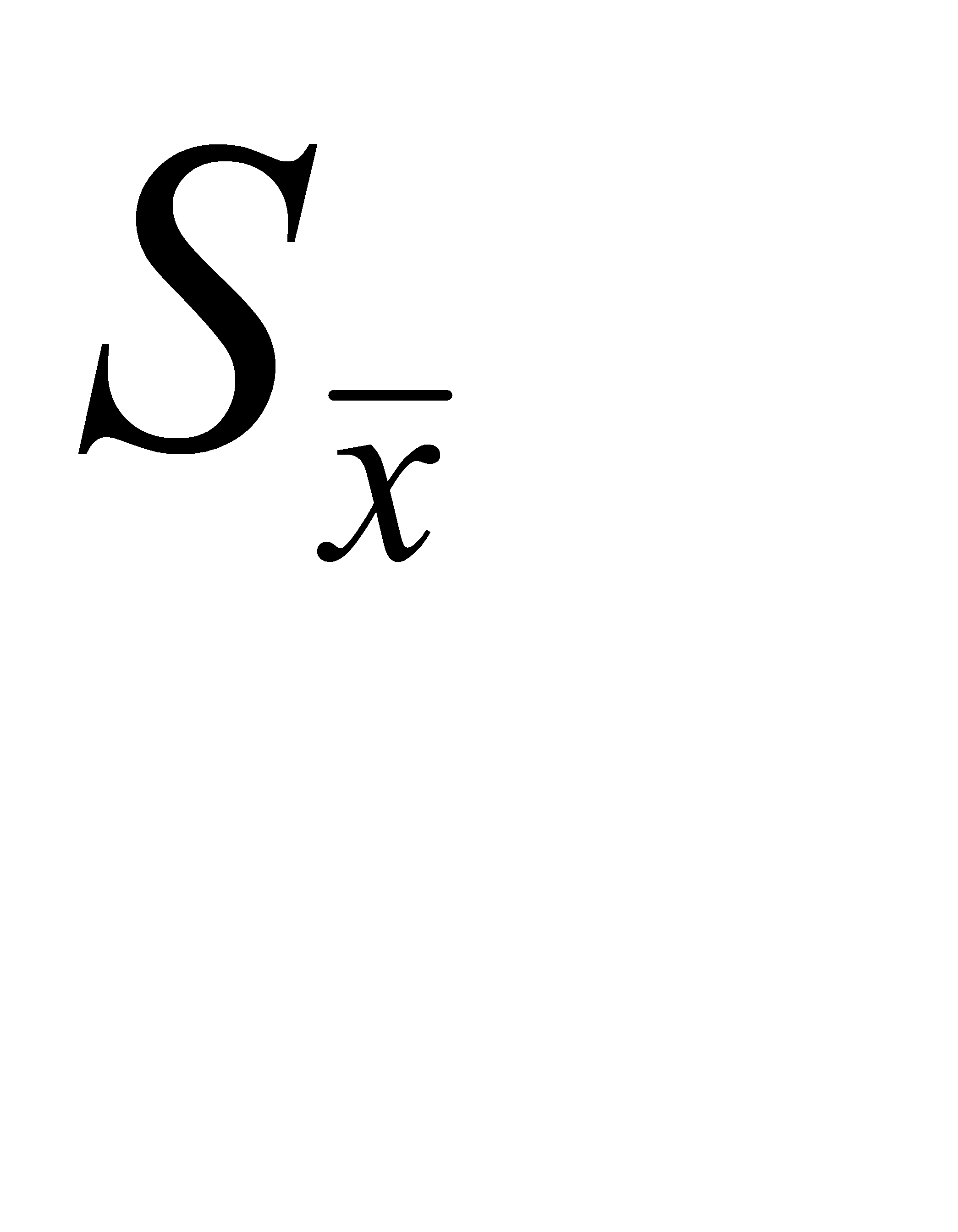 . Величина которой определяется по формуле
. Величина которой определяется по формуле
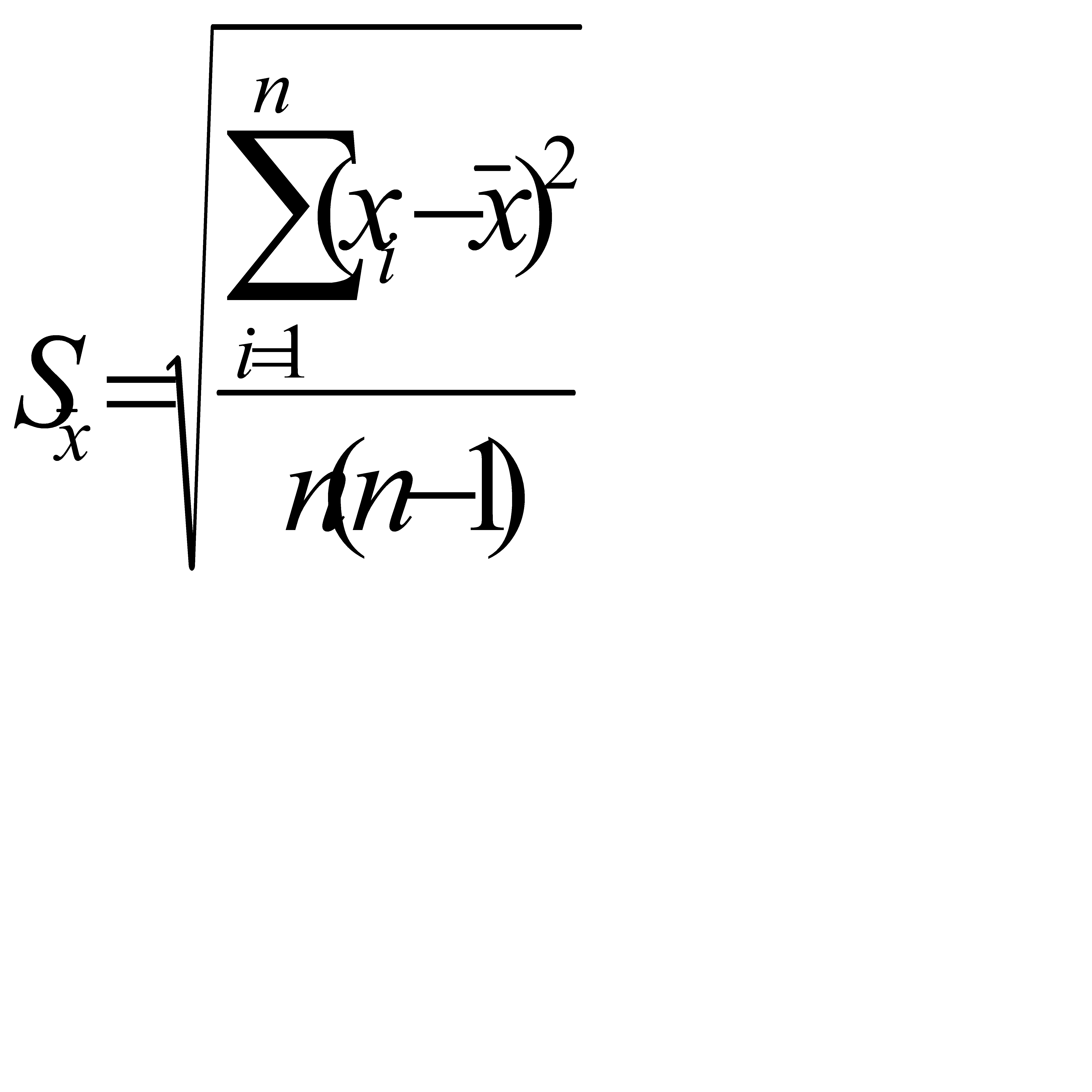 ,
,
где 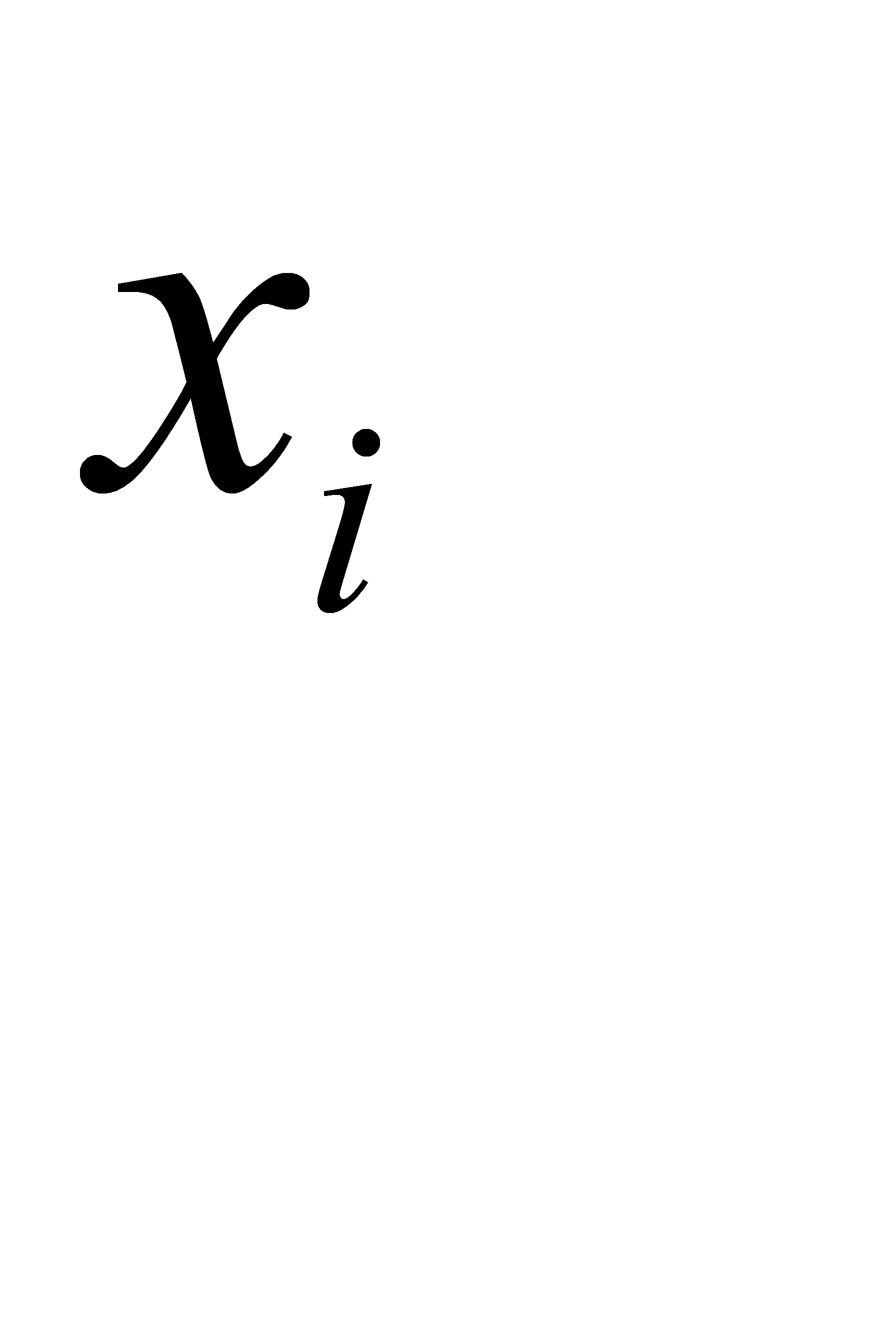 - результат i-го измерения;
- результат i-го измерения; 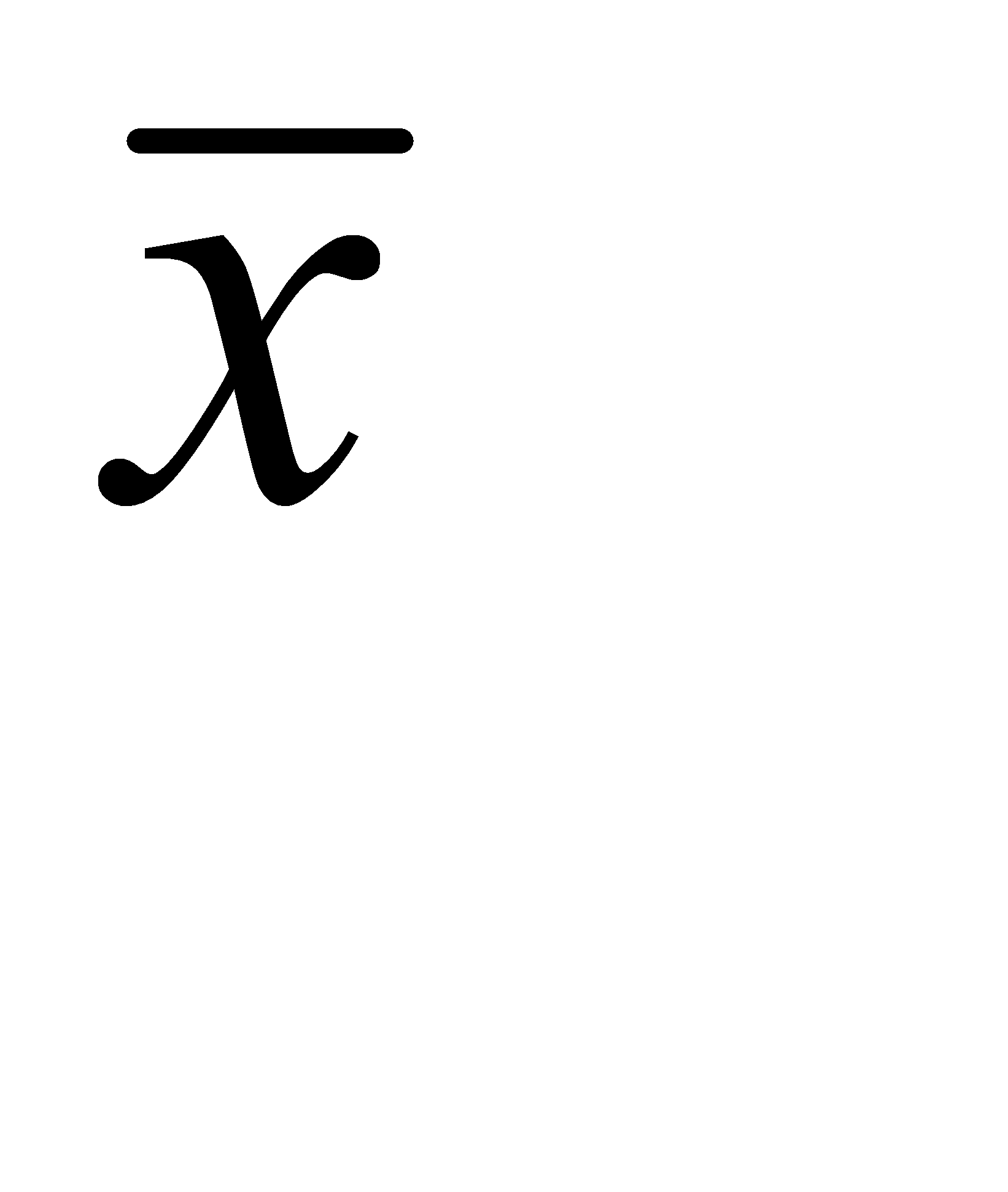 - среднее арифметическое полученных значений; n – число измерений.
- среднее арифметическое полученных значений; n – число измерений.
Чем больше число измерений, тем меньше 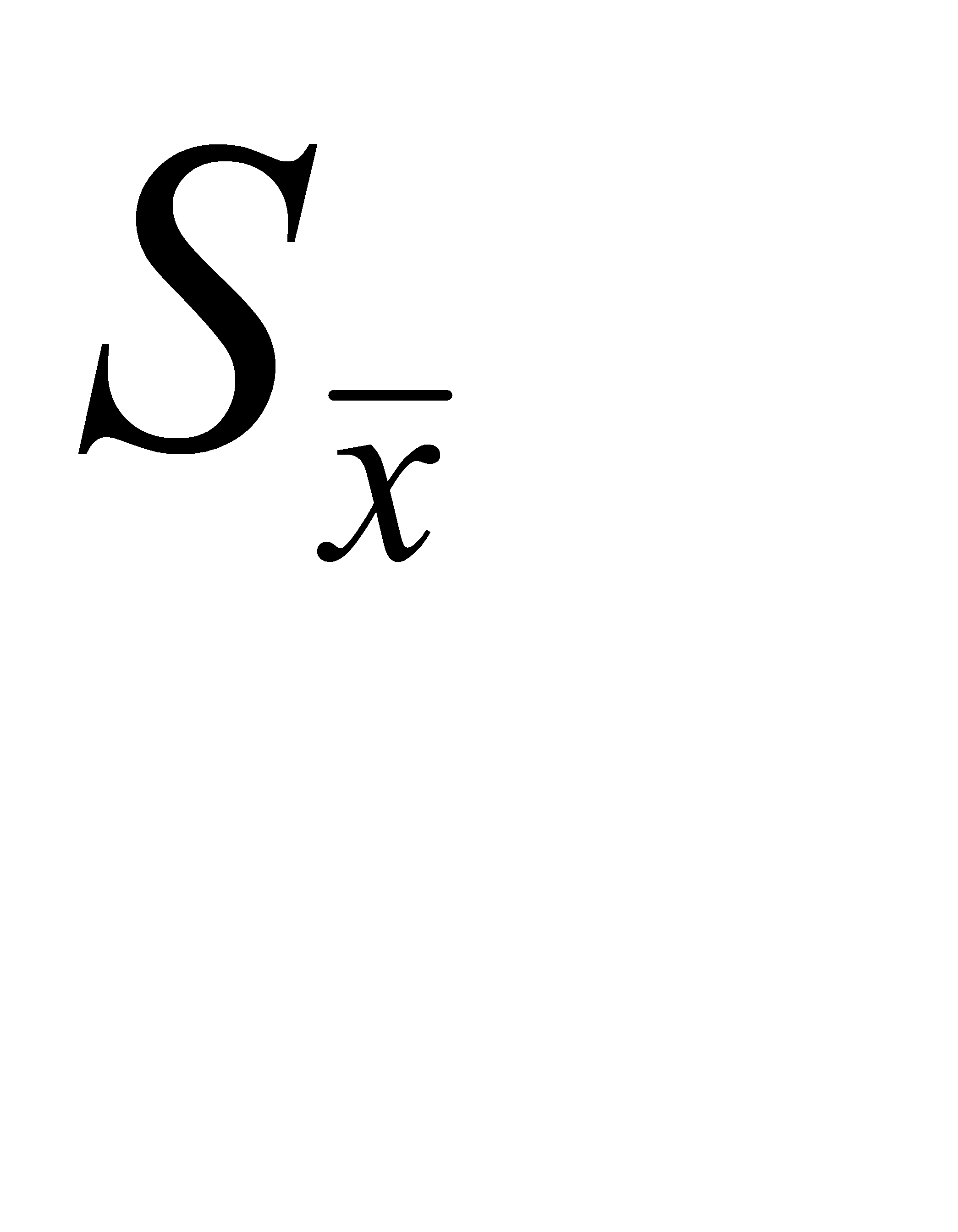 и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений
и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений 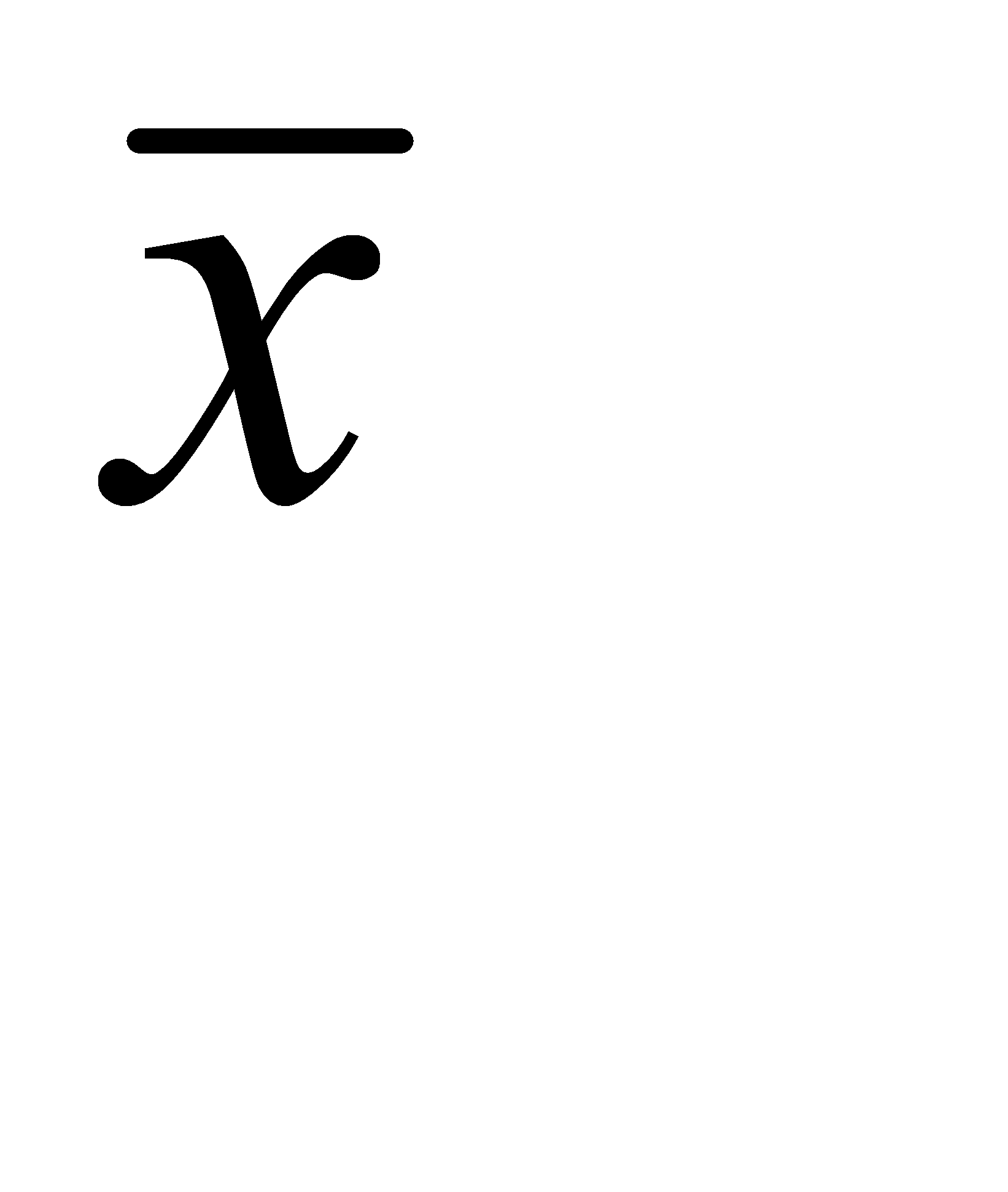 , а случайная абсолютная погрешность
, а случайная абсолютная погрешность  , то результат измерений запишется в виде
, то результат измерений запишется в виде  .
.
Интервал значений от 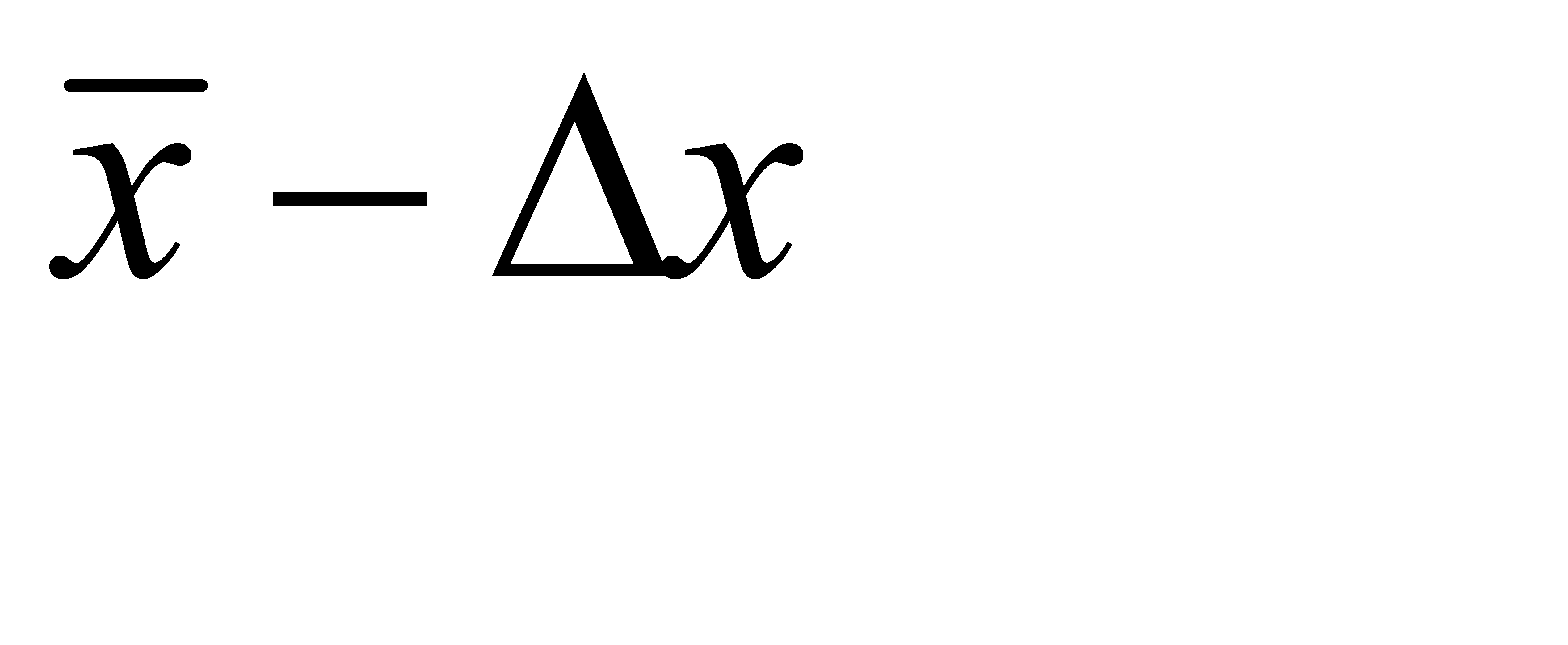 до
до  , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку
, в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку  является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью, или надежностьюизмерений. Эта величина численно равна площади заштрихованной криволинейной трапеции.
является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью, или надежностьюизмерений. Эта величина численно равна площади заштрихованной криволинейной трапеции.
Все это справедливо для достаточно большого числа измерений, когда 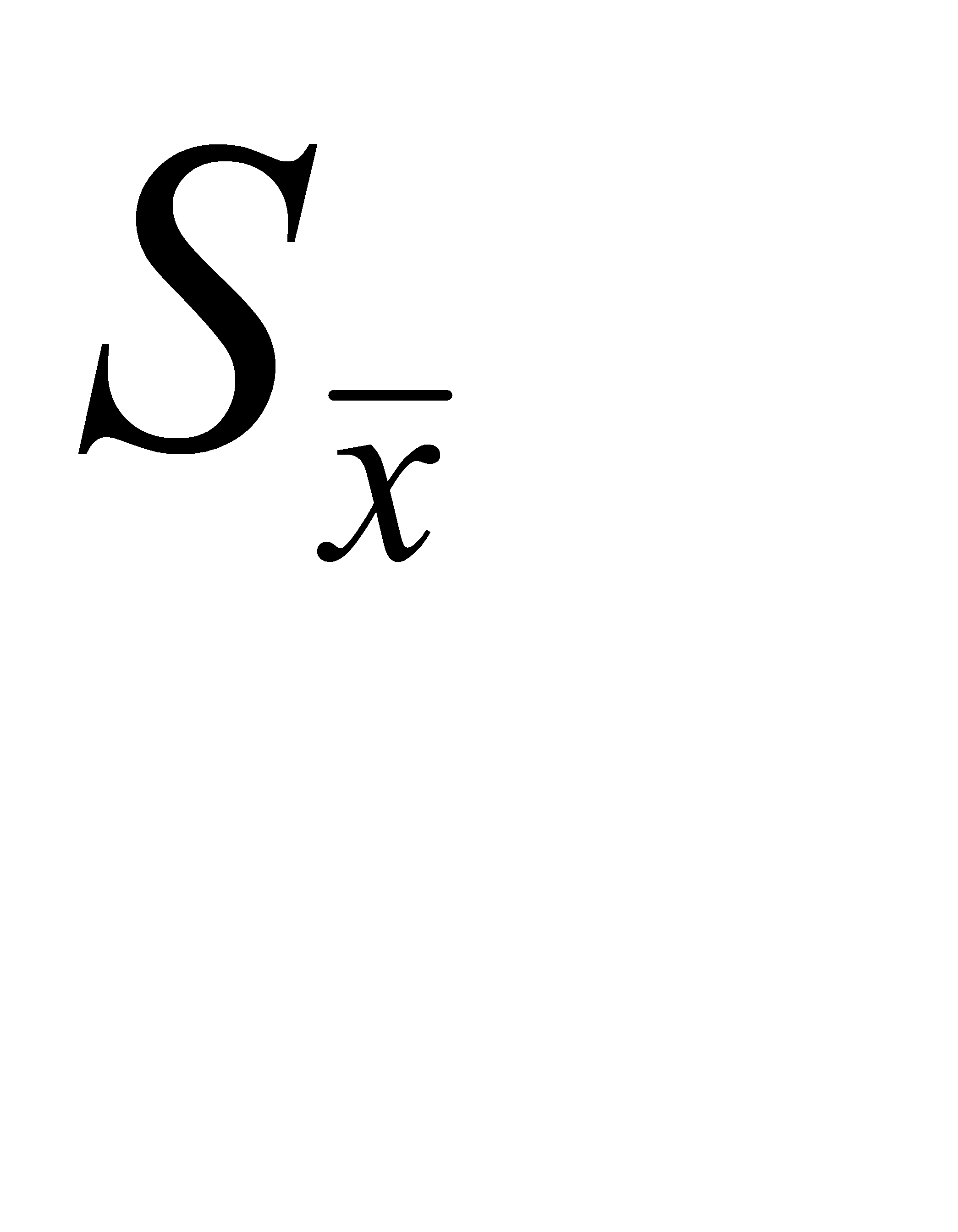 близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента.Это распределение вероятностей случайной величины
близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента.Это распределение вероятностей случайной величины 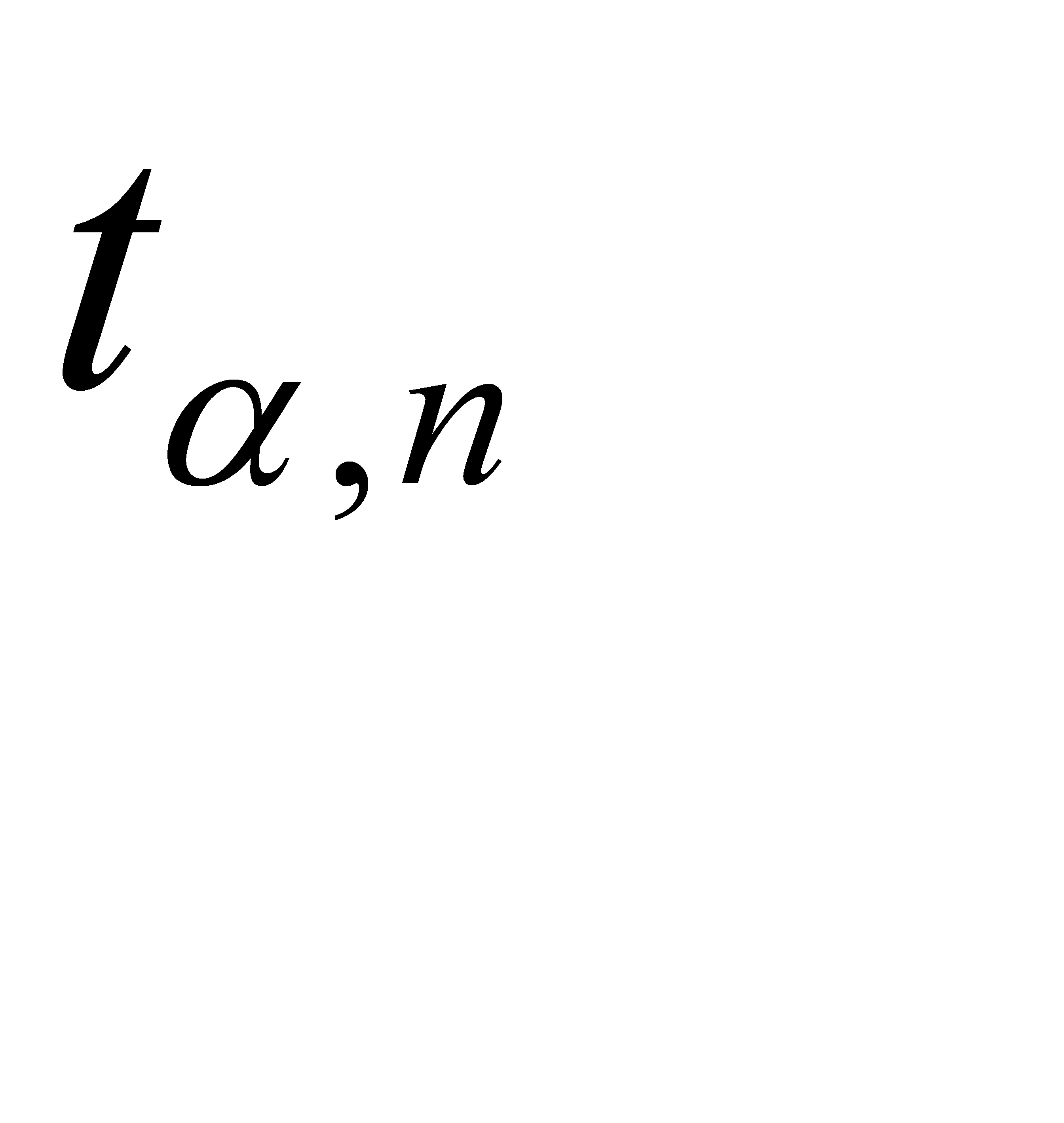 , называемой коэффициентом Стьюдента, дает значение доверительного интервала
, называемой коэффициентом Стьюдента, дает значение доверительного интервала  в долях средней квадратичной ошибки среднего арифметического
в долях средней квадратичной ошибки среднего арифметического 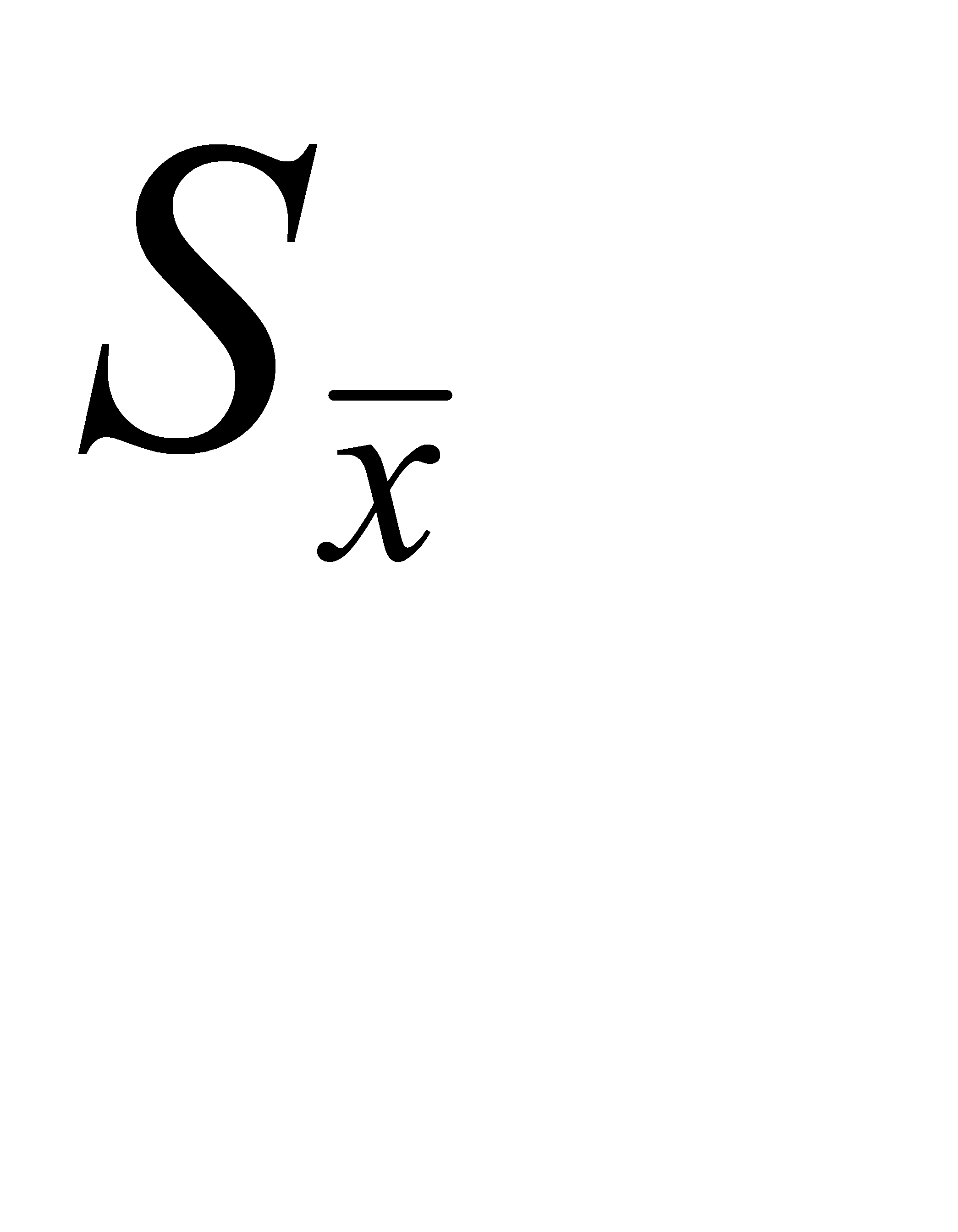 .
.
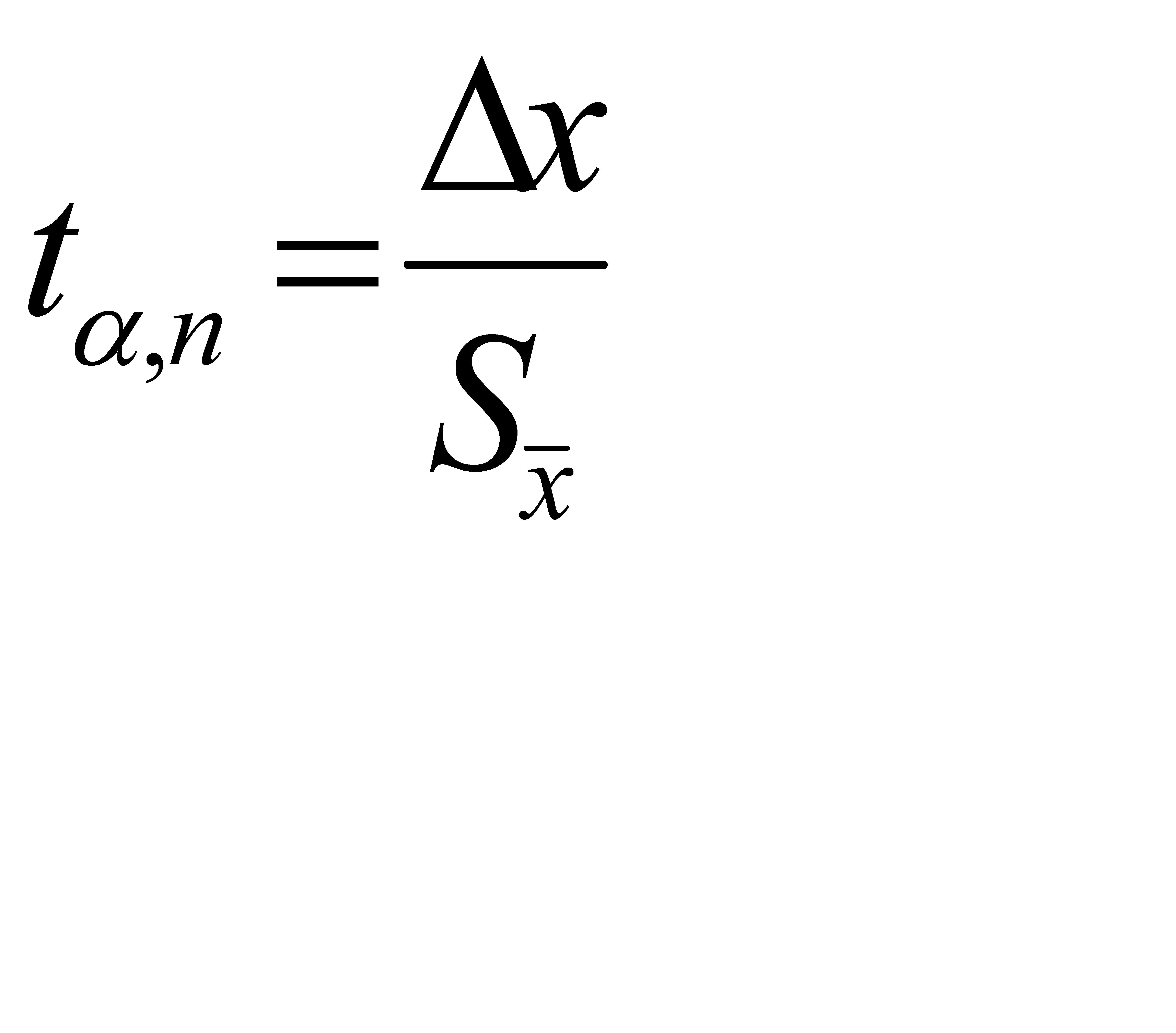
Распределение вероятностей этой величины не зависит от σ2, а существенно зависит от числа опытов n. С увеличением числа опытов nраспределение Стьюдента стремится к распределению Гаусса.
Функция распределения табулирована (табл.2.3). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α.
Функция распределения Стьюдента-Гаусса приведена в таблице 2.3.
Таблица 2.3.- функция распределения Стьюдента-Гаусса
| n | α | n | α | ||||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,8 | 0,9 | 0,95 | 0,98 | ||
| 1,9 | 2,9 | 4,3 | 7,0 | 1,5 | 2,0 | 2,6 | 3,4 | ||
| 1,6 | 2,4 | 3,2 | 4,5 | 1,4 | 1,9 | 2,4 | 3,1 | ||
| 1,5 | 2,1 | 2,8 | 3,7 | 1,4 | 1,9 | 2,4 | 3,9 |
Пользуясь данными таблицы, можно:
1) определить доверительный интервал, задаваясь определенной вероятностью;
2) выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции 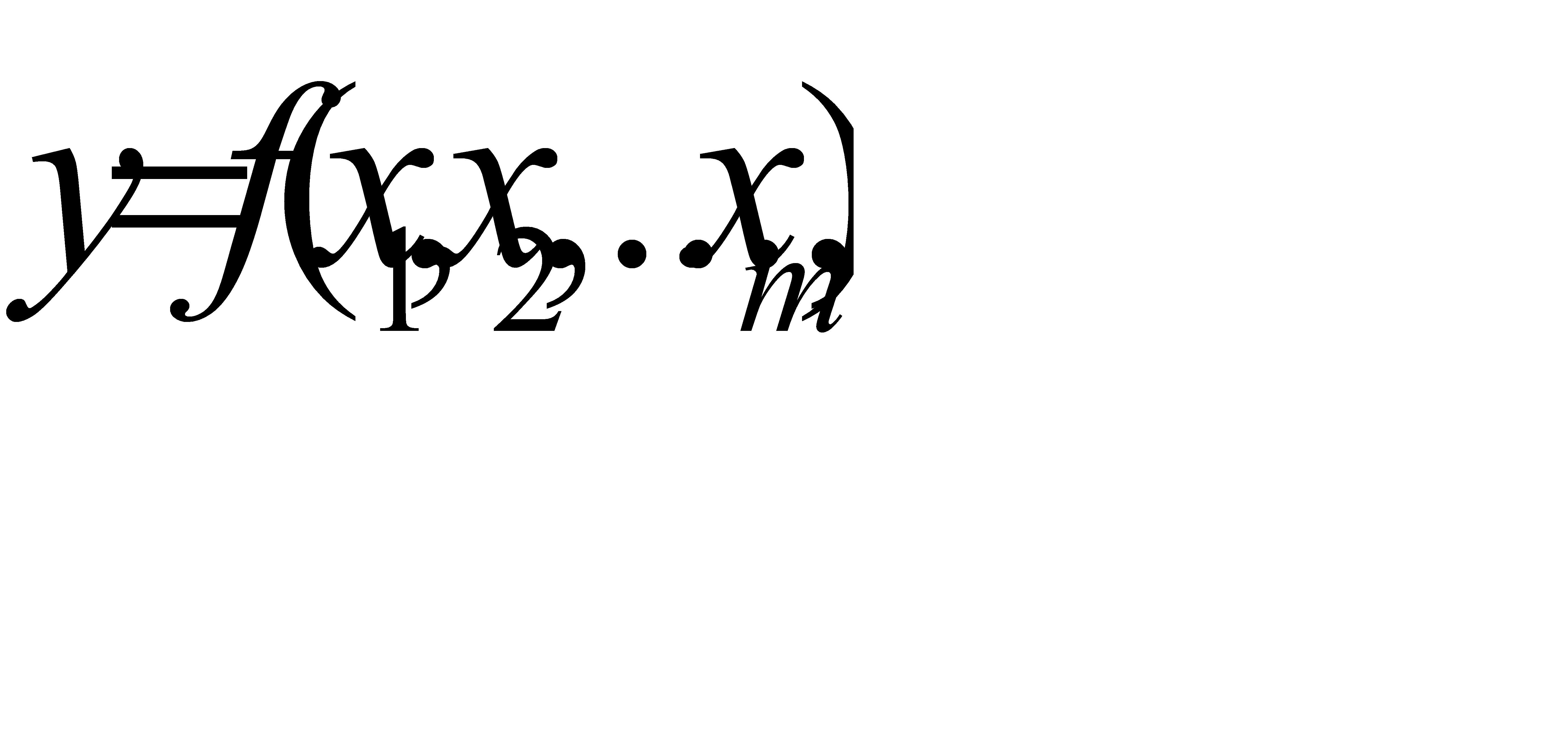 вычисляют по формуле
вычисляют по формуле

Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
Дата добавления: 2014-12-20; просмотров: 2429;
