Колебательный контур.

Электрические колебания возникают в колебательном контуре. который представляет собой совместно включенные индуктивность L и ёмкость С, рис.11.

Идеальным называется колебательный контур, не обладающий активным

сопротивлением. Колебания тока и напряжения в нем незатухающие.

Рассмотрим процессы в колебательном контуре, рис.12.

Если зарядить конденсатор и дать ему возможность разряжаться через катушку индуктивности, то в контуре возникнут электрические колебания. На рис.12 изображены колебания напряжения на обкладках конденсатора u _C и тока в контуре i_K.

В момент времени 1 конденсатор заряжен (состояние а) и подключен к катушке индуктивности. начинается разрядка конденсатора.

Напряжение на конденсаторе убывает, а ток в контуре постепенно возрастает,

так как ЭДС самоиндукции, возникающая в катушке, препятствует мгновенному нарастанию тока.

К моменту времени 2 ток в цепи достигает максимального значения, а напряжение на конденсаторе падает до нуля (состояние Ь). Ток должен был бы прекратиться, но как только он начинает убывать, в катушке .возникает ЭДС самоиндукции, препятствующая убыли тока. Пунктиром показаны силовые линии магнитного поля катушки (соленоида). Вследствие этого ток в контуре убывает постепенно, и происходит перезарядка конденсатора (состояние с).

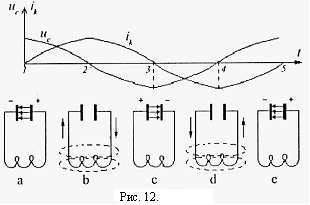Вторая половина периода протекает аналогично. Колебательный процесс в контуре совершается за счет энергии, сообщенной конденсатору.

В реальном колебательном контуре происходит потеря вследствие выделения тепла на активном сопротивлении проводов катушки, при поляризации диэлектрика в конденсаторе и при излучении электромагнитного поля в окружающее пространство. В результате этого колебания в реальном колебательном контуре будут затухающими.

В любой момент времени

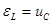
где- 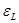-ЭДС самоиндукции в катушке. По закону электромагнитной индукции Фарадея.

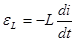
Из определения емкости следует

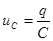
где q – величина заряда на одной пластине конденсатора.

Приравнивая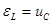

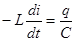, но так как 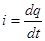, то

Следовательно

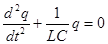
Обозначим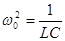

Получили дифференциальное уравнение гармонических колебаний заряда на пластинах конденсатора в идеальном колебательном контуре.

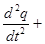
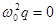
Решение этого уравнения имеет вид q=q_mcosω₀ t,

где q_m - максимальный заряд на пластине конденсатора, ω_{0 –} собственнаяциклическая частота колебательного контура.

Напряжение на пластинах конденсатора

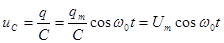, где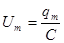

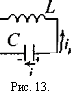Обычно за ток в контуре принимают ток, текущий через индуктивность, который направлен противоположно току через емкость (току смещения), рис.13.

, где Im=qmω0.

Так как 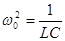= 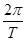где Т - период. колебаний в контуре, то

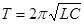- формула Томсона для собственной частоты совпадает с формулой для резонансной частоты в цепи с ёмкостью и индуктивностью. Следовательно, в колебательном контуре устанавливаются колебания с резонансной частотой.