Скалярное и векторное умножение векторов
Скалярным произведением двух векторов A и B называется произведение их модулей на косинус угла между ними. Скалярное произведение обозначается точкой. Результатом скалярного произведения является скаляр. Т.е.
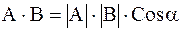
В координатной форме скалярное произведение векторов записывается как

В MathCAD для выполнения скалярного произведения на панели Matrix существует специальная кнопка скалярного произведения векторов, которая обозначена как 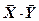 . Например:
. Например:
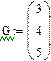
|
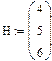
|
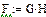
|
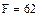
|
Векторным произведением двух векторов A и B называется третий вектор, модуль которого равен произведению модулей векторов A и B на синус угла между ними, а сам вектор перпендикулярен плоскости, в которой лежат исходные вектора, и направлен в ту сторону, откуда наименьший поворот первого вектора ко второму вектору виден происходящим против часовой стрелки. Т.е.
 ,
, 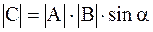
В координатной форме векторное произведение векторов A и B записывается как

В MathCAD для выполнения векторного произведения на панели Matrix существует специальная кнопка скалярного произведения векторов, которая обозначена как 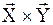 . Например:
. Например:

|
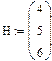
|
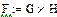
|
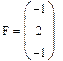
|
2 Решение систем линейных уравнений
В геодезии при уравнивании различных геодезических построений возникают так называемые нормальные уравнения, которые относятся к классу линейных уравнений вида
AX=B,
где A – квадратная симметричная матрица коэффициентов размера NxN, B – вектор свободных членов, X – вектор неизвестных.
Из общего курса линейной алгебры известно, что такая система линейных уравнений имеет единственное решение, если матрица A является невырожденной или, иначе, несингулярной, т.е. ее определитель не равен нулю. Такие матрицы называются еще хорошо обусловленными.
В MathCAD имеется целый ряд инструментов для решения хорошо обусловленных систем линейных уравнений. Рассмотрим эти инструменты по порядку.
Вариант 1 Непосредственное решение
Дана система линейных уравнений
AX=B
Для ее решения достаточно умножить левую и правую части уравнения на обратную матрицу A-1. В результате получим
X= A-1 B
Пример 1.
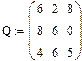
|
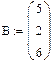
|
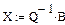
|

|
Вариант 2 Вычислительный блок given/find
Сформировать матрицу коэффициентов A, вектор свободных членов B и вектор начальных значений неизвестных либо записать систему уравнений в развернутом виде. В качестве начальных значений можно принять нулевой вектор. Затем записать:
given
AX=B
find(X)=
После этого в правой части появится вектор решения системы.
Следует обратить внимание на то, что при записи системы уравнений необходимо использовать знак равенства, который находится на панели логических операций либо использовать сочетание клавиш <Ctrl> +< =>.
Данный способ можно использовать для решения систем уравнений с хорошо обусловленной матрицей A. Это объясняется тем, что решение системы в данном случае производится методом итераций. И при хорошо обусловленной матрице коэффициентов итерации сходятся к единственному решению. В противном случае решение может не получится.
Пример 2.
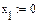
|
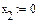
|
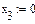
|
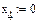
|
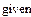
|
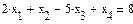
|

|

|
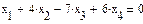
|
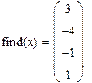
|
Пример 3
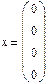
|
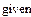
|
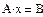
|
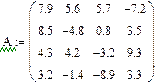
|
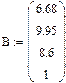
|
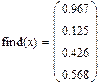
|
Вариант 3 Использование встроенной функции lsolve
Дана система уравнений в матричном виде
A*B=X
Решение системы также может быть найдено в матричном виде, как
X:=A-1B
Для этого может быть использована встроенная функция lsolve(A,B), где A – матрица коэффициентов системы линейных уравнений, B – вектор свободных членов.
Обращение к функции выглядит следующим образом
X:=lsolve(A,B).
Пример 4
Дана та же самая система линейных уравнений, как и в примере 3. Но для ее решения используем встроенную функцию lsolve.
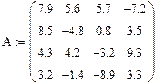
|
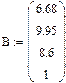
|

|
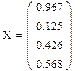
|
Вариант 4 Использование встроенной функции rref
Пусть задана система линейных уравнений, которая в матричном виде имеет вид
A*B=X
Решение системы находится как и в варианте 3
X:=A-1B
Однако решение производится с использованием встроенной функции rref. Для ее использования первоначально необходимо сформировать расширенную матрицу C, сделав вектор B четвертым столбцом матрицы A с помощью функции augment.
C:=augment(A,B)
Затем с помощью функции rref вычислить вспомогательную матрицу C1
C1:=rref(C)
После этого выбрать из C1 вектор-решение X
X:=C1<4>,
т.е. решение –это четвертый столбец матрицы C1.
3 Символьные операции с матрицами
Возможность MathCAD производить не только численные вычисления, но и символьные, позволяет выполнять символьные вычисления над матрицами.
Пусть задана некоторая матрица Q. Вычислим в символьном виде ее определитель. Для этого достаточно щелкнуть левой кнопкой мыши по обозначению определителя на панели Matrix и на рабочем столе появится шаблон, в котором на месте местозаполнителя запишем матрицу Q. После этого введем знак символьного равенства и получим определитель матрицы Q в символьном виде.
Пример 1. Вычисление определителя в символьном виде
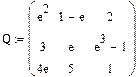
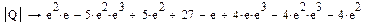
Пример 2. Вычисление определителя и обратной матрицы в символьном виде
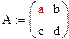
|
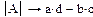
|
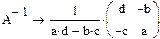
|
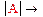
|

|
Пример 3. Перемножение матриц в символьном виде
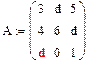
|

|
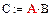
|

|
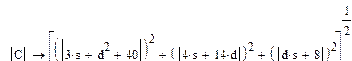
4 Решение нелинейных уравнений
4.1. given/find
4.2 меню
4.3 root
Дата добавления: 2014-12-20; просмотров: 1389;
