Цепь с последовательным соединением активного, индуктивного и емкостного сопротивления
В лекциях 4, 5 и 6 рассматривались идеальные цепи переменного тока с одним активным, индуктивным и емкостным сопротивлениями. На самом же деле всякая цепь переменного тока имеет все виды сопротивлений. Однако в практических расчетах обычно пренебрегают сопротивлениями с относительно небольшими значениями.
Представим себе неразветвленную цепь переменного тока с активным, индуктивным и емкостным сопротивлениями, распределенными равномерно по всей цепи (рис. 15).
В виду того, что ток в любом сечении цепи один и тот же и определяются суммарным действием всех имеющихся сопротивлений, цепь с равномерным распределением R, xL и хс условно можно заменить тремя последовательно соединенными сопротивлениями (рис. 16).
В подобной эквивалентной цепи расчетная величина тока будет такой же, как и в цепи рисунка 15.
Для мгновенных значений напряжения и э.д.с. в цепи (рис. 16) можно написать уравнение второго закона Кирхгофа
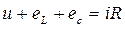, (46)
где и – приложенное к цепи напряжение;
eL – э.д.с. самоиндукции;
ес – э.д.с. емкости.
Отсюда
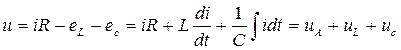. (47)
Здесь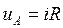 
- мгновенное напряжение, приложенное к активному сопротивлению R;
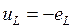- мгновенное напряжение, приложенное к индуктивному сопротивлению 
;
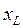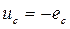- мгновенное напряжение, приложенное к емкостному сопротивлению 
.
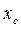При синусоидальном токе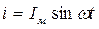 
иА будет совпадать по фазе с током, иL – опережать ток на угол 
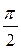и ис – отставать от тока на угол .
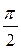Поэтому можно написать
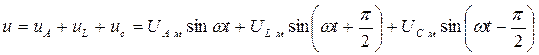. (48)
При сложении синусоидальных величин одинаковой частоты получается синусоидальная величина той же частоты с амплитудой, равной геометрической сумме амплитуд слагаемых синусоид. Поэтому алгебраическое сложение синусоид можно заменить геометрическим сложением векторов, представляющих синусоидальные величины:
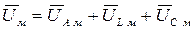. (49)
Вместо амплитуд можно взять действующие значения.
Тогда получим
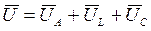(50)
На рисунке 17 показаны векторная (а) и волновые (б) диаграммы напряжений и тока.
Вектор тока I принят за исходный. По отношению к нему откладываются все остальные векторы: вектор UA, совпадающий с вектором тока; вектор UL, опережающий вектор тока на угол 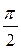; вектор UC, отстающий от вектора тока на угол 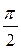. Диаграмма построена в предложении, что хL > xC, т.е. UL > UC (в сетях переменного тока индуктивные нагрузки преобладают над емкостными).
В результате геометрического сложения векторов UA, UL и UC получим вектор U приложенного к цепи напряжения. Вектор UA представляет активную, вектор UL – индуктивную, вектор UC – емкостную и вектор Ux – реактивную составляющую напряжения U.
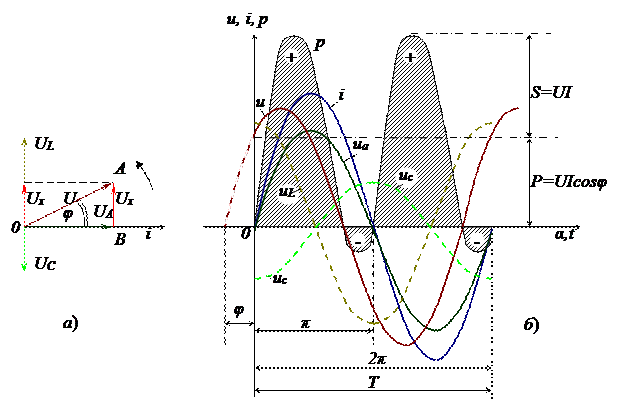
а – векторная; б – волновые.
Рисунок 17 – диаграммы цепи с последовательным соединением сопротивлений
Как видно из рисунка 17, вектор тока I отстает по фазе от приложенного напряжения U на угол φ.
Треугольник ОАВ называется треугольником напряжений. Сумма напряжений на индуктивном и емкостном сопротивлениях называется реактивным напряжением Ux.
Из треугольника ОАВ следует:
.
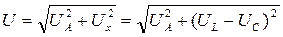Из выражений (17), (29) и (39) вытекает:
; 
; 
.
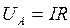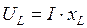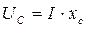Следовательно,
,
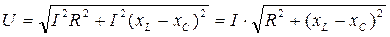откуда
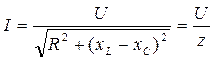. (51)
Выражение (51) представляет закон Ома для цепей с последовательным соединением активного, индуктивного и емкостного сопротивлений.
Величина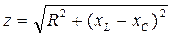 
называется полным или кажущимся сопротивлением цепи и измеряется в Омах.
Величина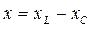 
носит название реактивного сопротивления цепи.
При хL > xC, напряжение UL > UC и угол φ будет положительным (вектор напряжения U откладывается вверх от исходного вектора тока I по направлению вращения векторов). В этом случае ток I отстает по фазе на угол φ от напряжения U.
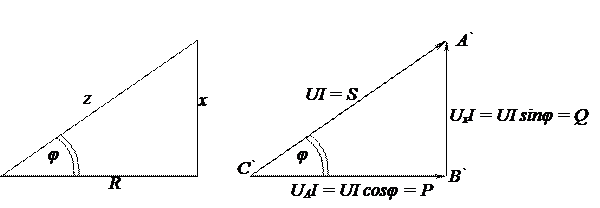
Рисунок 18 – Треугольник сопротивлений Рисунок 19 – Треугольник мощностей
При хL < xC, напряжение UL < UC и угол φ будет отрицательным (вектор напряжения откладывается вниз от исходного вектора тока I против направления вращения векторов). В этом случае ток I опережает по фазе на угол φ приложенное напряжение U.
Из треугольника ОАВ следует:
; 
; 
.
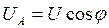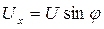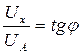Разделив все стороны треугольника напряжений ОАВ на величину тока I, получим подобный треугольник сопротивлений (рис. 18), так как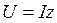 
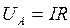, и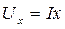 
.
Из треугольника сопротивлений следует:
; 
; 
; 
.
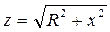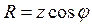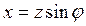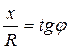Умножая ординаты тока и напряжения, можно получить кривую мгновенной мощности. Кривые, показанные на рис. 17, б, позволяют сделать следующие выводы:
- когда ток и напряжение имеют одинаковые знаки, мощность положительна. При этом часть энергии, посылаемой генератором в цепь, при возрастании тока накапливается у потребителя (в индуктивности) в виде энергии магнитного поля. Увеличение энергии магнитного поля в индуктивности потребителя происходит также за счет уменьшения энергии электрического поля конденсатора, которая переходит в магнитную энергию.
- когда ток и напряжение имеют разные знаки, мощность отрицательна, так как при уменьшении тока часть энергии магнитного поля, накопленная у потребителя, возвращается обратно генератору. Другая часть энергии магнитного поля потребителя (индуктивности) переходит в энергию электрического поля (конденсатора).
Мгновенная мощность переменного тока цепи, указанной на рис. 16, будет
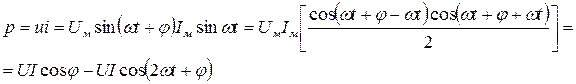(52)
Из выражения (52) следует, что мгновенная мощность состоит из двух величин: постоянной слагающей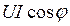 
, не зависящей от времени, и переменной – 
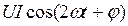с амплитудой UI, изменяющейся с двойной частотой по отношению к току и напряжению (рис. 17, б).
Средняя мощность за период, называемая активной мощностью, будет равна
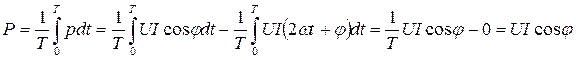(53)
Конус угла сдвига между током и напряжением называется коэффициентом мощности.
Как вытекает из формулы (53), при заданных значениях напряжения и тока величина активной мощности в цепи будет зависеть от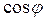 
.
Произведение UI называется полной или кажущейся мощностью и выражается в вольт-амперах (ва) или киловольт-амперах (ква).
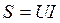(54)
Подставляя значение S из (54) в (53), получим активную мощность
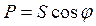. (55)
Если все стороны треугольника напряжений ОАВ (рис. 17, а) умножить на величину тока I, то можно получить подобный треугольник мощностей (рис.19).
Здесь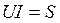 
– полная или кажущаяся мощность;
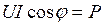– активная мощность;
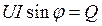– реактивная мощность.
Из треугольника О/А/В/ следует:
; 
; 
; 
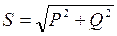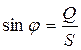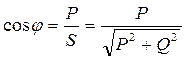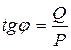. (56)
Если в цепи переменного тока имеется несколько последовательно соединенных активных, индуктивных и емкостных сопротивлений (рис. 20, а), то такую цепь можно представить в виде эквивалентной цепи (рис. 20, б). здесь активные, индуктивные и емкостные сопротивления сгруппированы, поэтому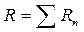 
; 
; 
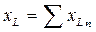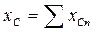. От схемы рис. 20, б можно перейти к эквивалентной схеме, показанной на рис. 20, в. Величину тока в такой цепи можно определить по формуле (51).
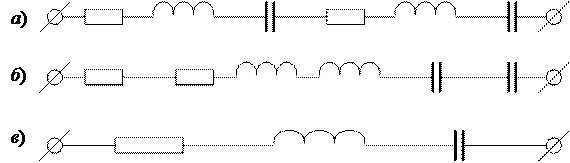
Рисунок 20 – Цепь с последовательным соединением нескольких сопротивлений
Лекция №8
Дата добавления: 2014-12-20; просмотров: 3329;