Цепь переменного тока с емкостью.

Как известно из курса физики, совокупность двух проводников, разделенных слоем диэлектрика, называется конденсатором и представляет собой электрическую емкость.

Следовательно, всякая электрическая линия передачи (воздушная или кабельная) может рассматриваться как некоторая система конденсаторов или емкость.

Особенно большой емкостью обладают кабельные линии. Если приложить к кабелю периодически изменяющееся напряжение и оставить разомкнутым все его жилы в конце линии, то в кабеле, при его значительной длине, будут непрерывно циркулировать зарядно-разрядные токи.

Представим себе электрическую цепь переменного тока, в которую включен конденсатор с емкостью С (рис. 13).

Активное и индуктивное сопротивления будем считать равными нулю.

Пусть генератор имеет синусоидальное напряжение

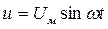. (34)

При повышении напряжения электрические заряды будут притекать к обкладкам конденсатора, заряжая его. Вследствие появления зарядов на обкладках конденсаторов появится э.д.с. емкости, которая в любой момент времени равна и противоположна по знаку приложенному напряжению.

Рисунок 13 – Цепь с емкостью.

При понижении напряжения заряды будут стекать с обкладок обратно к генератору.

Под влиянием сил переменного электрического поля между обкладками конденсатора в атомах диэлектрика происходит смещение электронов то в одну, то в другую сторону. Это направленное колебательное движение электронов в атомах диэлектрика представляет собой так называемый ток смещения.

Таким образом, в проводах, соединяющих генератор с конденсатором, будут циркулировать зарядный и разрядный токи проводимости, а в диэлектрике между обкладками конденсатора – токи смещения. Поэтому принято считать, что конденсатор как бы «пропускает» через себя переменный электрический ток.

Для любого момента времени можно написать

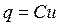, (35)

где q – заряд;

и – напряжение в данный момент времени.

Подставляя выражение (34) в (35), получим

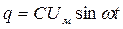. (36)

Производная 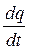будет представлять собой мгновенное значение тока, поэтому

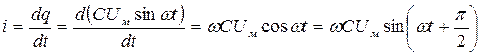. (37)

Из выражения (37) следует, что ток опережает по фазе напряжение на угол 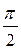(или на 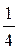периода).

Наибольшее значение i будет при 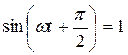, т.е.

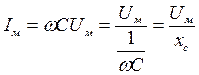. (38)

Разделив левую и правую части выражения (38) на 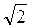, получим

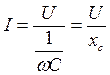. (39)

Выражения (38) и (39) представляют собой закон Ома для цепи переменного тока с емкостью. Здесь 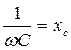носит название емкостного сопротивления, или реактивного сопротивления емкости, и измеряется в Омах.

.

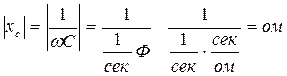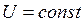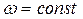Из формулы (38) и (39) следует, что величина тока при и зависит от емкости: при увеличении емкости ток возрастает, при уменьшении – убывает. Поэтому можно считать, что любой конденсатор ведет себя в цепи переменного тока как некоторое сопротивление.

На рисунке 14 показаны векторная (а) и волновые (б) диаграммы напряжения и тока.

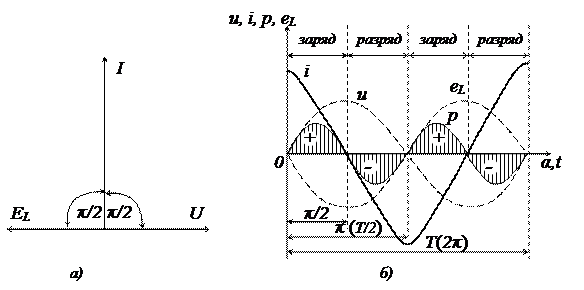
а – векторная; б - волновые

Рисунок 14 – Диаграммы цепи с емкостным сопротивлением

Для данной цепи составим уравнение по второму закону Кирхгофа

,

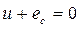так как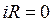

Отсюда 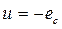, (40)

т.е. в любой момент времени мгновенное значение приложенного к цепи напряжения равно и противоположно по знаку э.д.с. емкости. Следовательно, все ординаты кривой э.д.с. емкости (в том числе и амплитуды) будут равны и противоположны по знаку ординатам кривой напряжения. Поэтому кривая е_L (см. рис. 14) будет сдвинута относительно кривой и на угол 180^о (или π). На такой же угол будут сдвинуты и векторы этих величин.

Мгновенная мощность в цепи переменного тока с емкостью будет равна

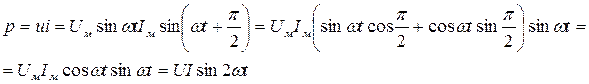(41)

Из выражения (41) следует, что мгновенная мощность изменяется в этом случае также по синусоидальному закону с двойной частотой. Кривую мгновенной мощности можно получить путем умножения ординат тока и напряжения (рис. 14).

Если отсчет времени (t = 0) для тока вести с момента, когда он будет равен нулю (как это сделано на рис. 12), то

;

;

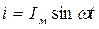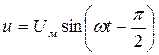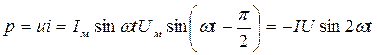. (42)

Отсюда следует, что ординаты кривой мгновенной мощности для цепи с емкостью равны (при равенстве х_L и х_с) и противоположны по знаку ординатам кривой мощности для цепи с индуктивностью, т.е. эти кривые сдвинуты между собой на угол π.

Из рисунка 14 видно, что в течение первой и третьей четвертей периода, когда напряжение возрастает от нуля до максимального значения, мощность положительна. Это значит, что генератор посылает энергию в конденсатор (конденсатор заряжается), где она накапливается в виде энергии электрического поля; при этом э.д.с. емкости направлена против тока.

В течение второй и четвертой периода, при убывании напряжения от максимального значения до нуля, мощность отрицательна. Это значит, что энергия , накопленная в электрическом поле конденсатора, при его разряде переходит в электромагнитную энергию и возвращается генератору; при этом э.д.с. емкости совпадает по направлению с током.

Таким образом, происходит непрерывный обмен энергией между генератором и конденсатором.

Средняя мощность генератора за период будет равна

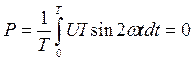. (43)

Следовательно, и энергия, отдаваемая генератором в сеть за период, будет также равна нулю. Поэтому в цепи с емкостью, точно также как и в цепи с индуктивностью, отсутствует необратимый процесс преобразования электрической энергии в тепловую или механическую.

Энергия, полученная конденсатором от генератора за четверть периода,

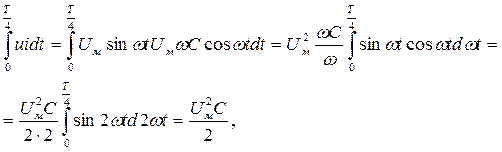(44)

т.е. она равна энергии, запасенной в электрическом поле конденсатора.

Мощность в цепи, содержащей только емкость, оценивается по ее наибольшему значению и называется реактивной мощностью.

Как следует из формулы (41), амплитуда мощности, или реактивная мощность будет равна, как и в случае цепи с индуктивностью:

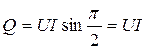. (45)

Обобщая изложенное, можно сделать следующие выводы:

- в цепя переменного ока только с емкостным сопротивлением (R = 0; L = 0) ток опережает по фазе приложенное напряжение на угол 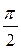, или на четверть периода во времени.

- закон Ома справедлив для амплитудных и действующих значений тока и напряжения. Сопротивлением в данном случае является величина 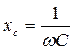, выражаемая в Омах и называемая емкостным сопротивлением или реактивным сопротивлением емкости. Это сопротивление – следствие противодействия внутреннего электрического поля диэлектрика конденсатора внешнему электрическому полю генератора, осуществляющему перенос электронов.

- при прохождении тока в цепи происходят колебания энергии от генератора к конденсатору и от конденсатора к генератору. Так как R = 0, то средняя мощность и энергия за период равны нулю.

Лекция №7