Теоретическая часть. При механическом воздействии тела изменяют свои размеры и форму, то есть деформируются

При механическом воздействии тела изменяют свои размеры и форму, то есть деформируются. Одним из видов деформации тела являются упругие деформации (растяжение – сжатие, сдвиг, кручение, изгиб), которые могут быть сведены к двум основным: растяжению или сжатию и сдвигу.

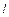Рассмотрим случай упругого растяжения прямого стержня под действием силы . В результате длина стержня увеличивается на величину 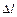, называемую абсолютной деформацией. Величиной, характеризующей деформацию стержня, принято считать относительную деформацию:

. (7.1)

Физическая величина, численно равная упругой силе , действующей перпендикулярно, на единицу площади сечения тела, называется нормальным напряжением:

. (7.2)

Р. Гук экспериментально установил, что при растяжении стержня его относительная деформация пропорциональна приложенному напряжению:

, (7.3)

где 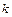– коэффициент упругости, зависящий от свойства материала. Величина , обратная коэффициенту упругости, называется модулем упругости, или модулем Юнга материала. Выясним физический смысл модуля Юнга. В выражении (7.3) предположим, что 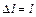, тогда . Следовательно, модуль Юнга численно равен нормальному напряжению, которое возникло бы в образце при увеличении его длины в два раза, при условии, что для этих деформаций выполняется закон Гука. На практике большинство материалов не выдерживают напряжений, соответствующих , и разрушаются. Область упругих деформаций составляет .

Деформацию сдвига проще всего осуществить, если взять пластину, имеющую форму прямоугольного параллелепипеда (рис. 7.1), и приложить к ней силу 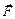, касательную к ее поверхности. Нижняя часть пластины должна быть закреплена. Под действием этой силы слои пластины сдвигаются друг относительно друга, причем величина сдвига тем больше, чем дальше отстоит слой от нижней закрепленной поверхности пластины. При этом боковые стороны пластины отклоняются на некоторый угол 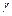. Считается, что действие силы 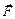равномерно распределено по площади верхнего основания пластины. Тогда величину напряжения можно считать равной отношению всей внешней силы 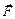к площади основания пластины 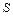: 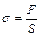. Относительная деформация сдвига определяется по формуле:

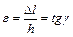, (7.4)

где 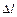– абсолютный сдвиг верхней грани пластины по отношению к нижней, – высота пластины. Для упругой деформации величина угла 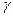мала, следовательно .

Для упругой деформации закон Гука можно записать в виде:

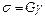. (7.5)

Постоянная 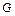называется модулем сдвига и зависит от природы материала, из которого изготовлена пластина.