Развертка поверхности прямой четырехугольной призмы

Полная развертка такой призмы (рис. 9.1) состоит из четырех прямоугольников, представляющих в истинном виде боковые грани призмы, и двух четырехугольников – ее верхнего и нижнего оснований.

Взяв произвольную прямую (рис. 9.2), отложим на ней произвольно отрезки, равные сторонам основания призмы AB, BC, CD, DA, истинные длины которых имеем на рис. 9.1. Затем проведя в точках A, B, C и D к прямой перпендикуляры, отложим на них длину боковых ребер (высоту) призмы и соединим полученные точки прямой. Построенный прямоугольник представит развертку боковой поверхности призмы.

Пристроив к одной из граней верхнее и нижнее основания призмы, получим полную развертку призмы.

Пересечем ту же призму фронтально проецирующей плоскостью a (рис. 9.1) и нанесем на развертку линию, по которой плоскость a пересечет поверхность призмы.

Для этого будет достаточно отметить на развертке точки 1, 2, 3 и 4, в которых боковые ребра призмы пересекаются плоскостью a, и каждые две смежные точки соединить прямой – это будут линии, по которым грани призмы пересекаются той же плоскостью.

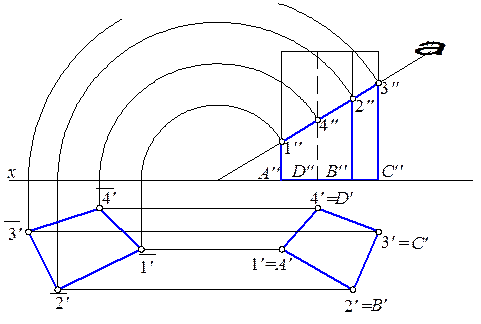
Рис. 9.1

Для получения полной развертки усеченной призмы необходимо определить способом совмещения истинный вид сечения и построить фигуру сечения на развертке к одной из граней призмы, что и выполнено на рис. 9.2.

Рис. 9.2