Механические характеристики

Уравнение механической характеристики:

(*)

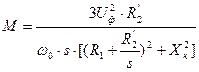Исследуем зависимость на экстремум,→ 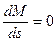, получаем две максимальные точки: М_к, s_к – критические.

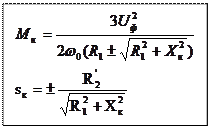
(+) – s >0 (двигательный режим)

(–) – s <0 (генераторный режим)

Чаще применяют более удобную формулу механической характеристики:

где a=R₁/R₂

Если ω→ +∞, s→ -∞, то М→0

ω→ -∞, s→ +∞, то М→0

Вывод: ось скорости является асимптотой механической характеристики. Для построения механической характеристики по паспортным данным используют упрощение: R₁=0. Получаем:

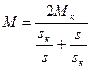- упрощенная формула Клосса.

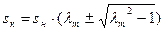
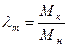где - перегрузочная способность

Рабочий участок характеристики (прямолинейный) можно построить по двум точкам (ω₀, М=0, s=0) и (ω_н, М_н, s_н).

Характерные точки (см. рисунок 4.2):

1) М=0, s=0, ω=ω₀ – точка идеального Х.Х.;

2) М=М _н, s=1, ω=0 – КЗ/пуск;

3) М_кд, s_кд; М_к2, s_к2 – критические точки;

4) s→±∞, ω→±∞, → М→0

Решение:

1) Угловая номинальная скорость, рад/с

ω_н=2πn_ном/60=2·3,14·1465/60=153,3

2) Угловая скорость идеального Х.Х., рад/с

ω₀=2πf₁/р=2·3,14·50/2=157

3) Номинальный момент, Н·м

М_ном=Р_ном/ ω_ном=15000/153,3=98

4) Номинальное скольжение

s_ном=(ω₀-ω_н)/ω₀=(157-153,3)/157=0,025

5) Критический момент АД, Н·м

М_к=λ_м·М_ном=2,3·98=225

6) Критическое скольжение

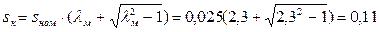
7) Пусковой момент, Н·м

М_п=λ_п·М_ном=1,1·98=107,6

АД может работать во всех энергетических режимах, которые определяются значением и знаком скольжения (рисунок 4.2):

1) s=0, ω=ω₀ – режим идеального Х.Х.;

2) s=1, ω=0 – режим КЗ;

3) 0<s<1, 0<ω<ω₀ – двигательный режим;

4) s<0, ω>ω₀ – генераторный режим;

5) s>1, ω<0 ( при ω₀>0) – противовключение;