Теплоемкость определяет количество теплоты, необходимое для изменения температуры системы на К, т.е. .
Поскольку количество теплоты 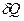 , необходимое для изменения температуры системы на
, необходимое для изменения температуры системы на 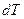 , зависит от характера происходящего при этом процесса, то и теплоемкость
, зависит от характера происходящего при этом процесса, то и теплоемкость 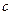 системы так же зависит от процесса. Это означает, что теплоемкость является не функцией состояния системы, а функцией процесса: одна и та же система в зависимости от происходящего в ней при нагревании процесса обладает различными теплоемкостями. Численно величина
системы так же зависит от процесса. Это означает, что теплоемкость является не функцией состояния системы, а функцией процесса: одна и та же система в зависимости от происходящего в ней при нагревании процесса обладает различными теплоемкостями. Численно величина 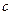 изменяется в пределах от
изменяется в пределах от 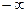 до
до 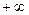 . Наибольшее практическое значение имеют теплоемкости
. Наибольшее практическое значение имеют теплоемкости 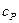 и
и 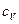 - теплоемкости для процессов при постоянном давлении и постоянном объеме. Теплоемкость величина аддитивная, поэтому в ТД чаще используются
- теплоемкости для процессов при постоянном давлении и постоянном объеме. Теплоемкость величина аддитивная, поэтому в ТД чаще используются
удельная теплоемкость – теплоемкость единицы массы вещества: 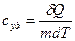 ,
,
и соответствующие ей удельные теплоемкости при постоянном давлении 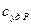 и объеме
и объеме 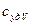 ,
,
молярная теплоемкость – теплоемкость одного моля вещества: 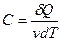 ,
,
и соответствующие ей молярные теплоемкости при постоянном давлении 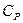 и объеме
и объеме 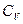 .
.
С определение теплоемкости тесно связано понятие о термостате. Термостат – тело с настолько большой теплоемкостью 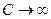 , что его температура при теплообмене с какой-либо системой не меняется. Когда говорят о системе помещенной в термостат, то имеют в виду систему, в которой при всех происходящих в ней процессах (расширение, намагничивание и т.д.) температура поддерживается постоянной.
, что его температура при теплообмене с какой-либо системой не меняется. Когда говорят о системе помещенной в термостат, то имеют в виду систему, в которой при всех происходящих в ней процессах (расширение, намагничивание и т.д.) температура поддерживается постоянной.
Первое начало ТД позволяет найти значения различных теплоемкостей и установить связь между ними, если известны термическое и калорическое уравнения состояния системы.
В общем случае внутренняя энергия 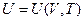 является функцией объема и температуры (калорическое уравнение), тогда приращение внутренней энергии, выраженное через приращение независимых переменных
является функцией объема и температуры (калорическое уравнение), тогда приращение внутренней энергии, выраженное через приращение независимых переменных 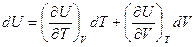 .
.
Первое начало ТД для одного моля вещества с учетом калорического уравнения состояния
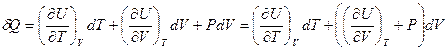 , отсюда
, отсюда
получим выражение для молярной теплоемкости:
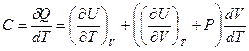 .
.
В качестве иллюстрации рассмотрим ТД процессы над идеальным газом. Получим выражения для молярных теплоемкостей идеального газа.
Опыт показал (Гей-Люсак и Джоуль-Томсон, поставили опыт по расширению газа в пустоту), что внутренняя энергия идеального газа, который подчиняется уравнению состояния идеального газа, зависит только от температуры 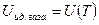 , и не зависит от занимаемого им объема.
, и не зависит от занимаемого им объема.
Для идеального газа термическим уравнением состояния является уравнение Менделеева-Клапейрона для одного моля вещества 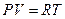 .
.
В процессе при постоянном объеме 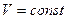 , приращение
, приращение 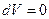 , тогда I начало ТД
, тогда I начало ТД
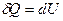
и 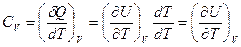 .
.
Результаты опыта показывают, что у одноатомных газов теплоемкость 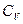 не зависит от температуры. Для других идеальных газов существует слабая зависимость теплоемкости
не зависит от температуры. Для других идеальных газов существует слабая зависимость теплоемкости 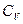 от температуры. Т.е. в широких температурных пределах можно считать для идеальных газов
от температуры. Т.е. в широких температурных пределах можно считать для идеальных газов 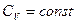 . Отсюда, учитывая, что для идеального газа внутренняя энергия является только функцией температуры
. Отсюда, учитывая, что для идеального газа внутренняя энергия является только функцией температуры 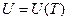 , и не зависит от объема, получим для идеальных газов калорическое уравнение состояния:
, и не зависит от объема, получим для идеальных газов калорическое уравнение состояния:
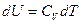
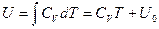 .
.
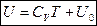
В процессе при постоянном давлении 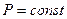 над идеальным газом первое начало ТД с учетом выражения
над идеальным газом первое начало ТД с учетом выражения 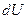 :
:
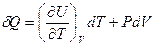 , тогда
, тогда
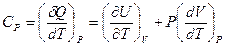
для одного моля идеального газа, учитывая уравнение состояния 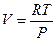 , и производные
, и производные 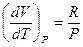 ,
, 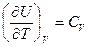 , получим
, получим 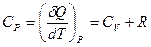 .
.
Дата добавления: 2019-10-16; просмотров: 677;
