Существование SDRE стабилизирующего управления
Прежде чем рассматривать использования SDRE стабилизирующего управления в задаче дифференциальной игры, приведем некоторые сведения, расширяющие ранее опубликованные результаты исследований [24,25,44, 45]. Пусть управляемая нелинейная система описывается уравнением
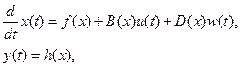 (2.52)
(2.52)
где 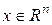 −состояние системы
−состояние системы 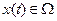 ,
, 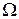 − открытое множество в
− открытое множество в 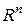 ,
, 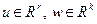 −управления и
−управления и 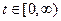 .
.
Функции 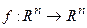 и
и 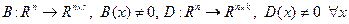 . Без потери общности, будем считать начало координат
. Без потери общности, будем считать начало координат 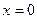 устойчивым состоянием покоя,
устойчивым состоянием покоя, 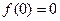 и
и 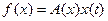 .
.
Задан функционал качества
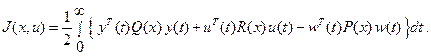 (2.53)
(2.53)
Отметим, что лагранжиан функционала (2.53) квадратичен по 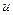 и
и 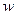 . Матрицы весов таковы, что
. Матрицы весов таковы, что
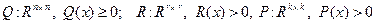 .
.
Предположение 2.7.1.Нелинейная система в постановке задачи (2.52), (2.53) стабилизируема и детектируема, если тройка 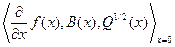 стабилизируема и детектируема.
стабилизируема и детектируема.
Определение 2.7.1.Будем называть представление нелинейной управляемой системы (2.52) в виде
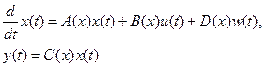 (2.54)
(2.54)
SDC-представлением.
Предположение 2.7.2. 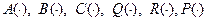 − матрицы
− матрицы 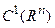 действительных переменных.
действительных переменных.
Предположение 2.7.3. SDC-представление нелинейной системы (2.52) является стабилизируемым (управляемым) в области 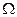 , если пары
, если пары 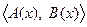 ,
, 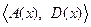 стабилизируемы (управляемы) в линейном смысле для
стабилизируемы (управляемы) в линейном смысле для 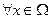 ., т.е.
., т.е.
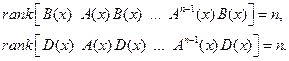
Это означает, что существует положительно определенная матрица 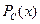 (грамиан управляемости) для всех
(грамиан управляемости) для всех 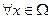 , являющаяся решением уравнения Ляпунова
, являющаяся решением уравнения Ляпунова
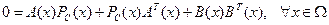 .
.
Предположение 2.7.4. SDC-представление нелинейной системы (2.52) является наблюдаемым и детектируемым в области 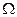 , если пара
, если пара 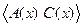 наблюдаема, а пара
наблюдаема, а пара 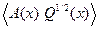 детектируема в линейном смысле для
детектируема в линейном смысле для 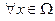 , т.е.
, т.е.
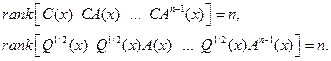
Это означает, что существует положительно определенная матрица 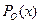 (грамиан наблюдаемости) для всех
(грамиан наблюдаемости) для всех 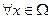 , являющаяся решением уравнения Ляпунова
, являющаяся решением уравнения Ляпунова
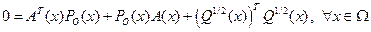 .
.
Управление объектом (2.52) осуществляется с использованием обратной связи в соответствии с законом
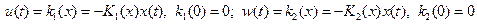 , (2.55)
, (2.55)
где 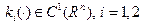 . Синтез управления, осуществляющего перевод системы (2.52) из начального состояния
. Синтез управления, осуществляющего перевод системы (2.52) из начального состояния 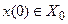 в состояние
в состояние 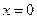 , т.е.
, т.е. 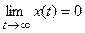 , и доставляющего минимум функционалу (2.53), заключается в нахождении соответствующих матриц
, и доставляющего минимум функционалу (2.53), заключается в нахождении соответствующих матриц 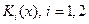 .
.
В соответствии с изложенным в предыдущей главе, искомые матрицы определяются соотношениями
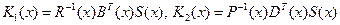 , (2.56)
, (2.56)
где положительно определенная матрица 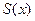 является решением уравнения Риккати с параметрами, зависящими от состояния,
является решением уравнения Риккати с параметрами, зависящими от состояния,
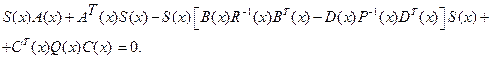 (2.57)
(2.57)
Определение 2.7.2. Матрица
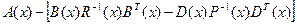
в SDC-представление вида (2.44) является поточечно гурвицевой в области 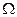 , если корни характеристического уравнения этой матрицы отрицательны (
, если корни характеристического уравнения этой матрицы отрицательны ( 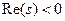 ) для всех
) для всех 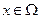 .
.
Система (2.52) управлениями (2.56) − (2.57) имеет вид
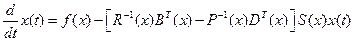 . (2.58)
. (2.58)
Определение 2.7.3. Будем называть метод синтеза управляющих воздействий для нелинейной системы вида (2.52) в ее SDC-представлении с квадратическим функционалом качества, что приводит к использованию уравнения Риккати с параметрами, зависящими от состояния, SDRE-методом.
Определение 2.7.4. Управления (2.55) реализуемы SDRE-методом в области 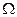 , если существует поточечно стабилизируемая SDC-параметризация
, если существует поточечно стабилизируемая SDC-параметризация 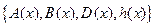 , поточечно положительно полуопределенная матрица
, поточечно положительно полуопределенная матрица 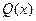 и поточечно положительно определенные матрицы
и поточечно положительно определенные матрицы 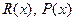 такие, что синтезированные управления являются функциями состояния объекта.
такие, что синтезированные управления являются функциями состояния объекта.
Предположение 2.7.5. Закон управления 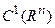 (2.54) реализуем SDRE-методом, если существует SDC-представление нелинейной системы (2.52) и матрицы штрафа функционала (2.53) таковы, что
(2.54) реализуем SDRE-методом, если существует SDC-представление нелинейной системы (2.52) и матрицы штрафа функционала (2.53) таковы, что 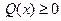 и
и 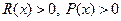 для
для 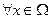 .
.
Теорема 2.7.1. [2]. Законы управления 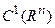 (2.54) реализуемы SDRE-методом, если существует SDC-представление нелинейной системы (2.52) такое, что матрица
(2.54) реализуемы SDRE-методом, если существует SDC-представление нелинейной системы (2.52) такое, что матрица 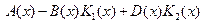 поточечно является матрицей Гурвица при
поточечно является матрицей Гурвица при 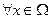 и нули замкнутой системы поточечно лежат в левой полуплоскости
и нули замкнутой системы поточечно лежат в левой полуплоскости 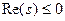 .
.
Теорема 2.7.1 представляет необходимые и достаточные условия для реализации закона управления SDRE-методом. Следует отметить сложность использования данной теоремы в случае неконечного числа SDC-представлений нелинейной системы.
Теорема 2.7.2. [2] Пусть нелинейная управляемая система описывается уравнением (2.52), где 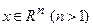 , и
, и 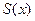 симметричная положительно определенная матрица, являющаяся поточечным решением матричного уравнения типа Риккати (2.56). Тогда, учитывая Предположение 2.7.2, SDRE-метод реализует локально асимптотическое устойчивое решение задачи управления в замкнутом виде.
симметричная положительно определенная матрица, являющаяся поточечным решением матричного уравнения типа Риккати (2.56). Тогда, учитывая Предположение 2.7.2, SDRE-метод реализует локально асимптотическое устойчивое решение задачи управления в замкнутом виде.
Доказательство. Воспользовавшись теоремой 2.4.1, запишем условие асимптотической устойчивости для SDC-представления нелинейной системы (2.52):
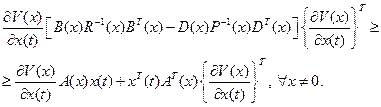 (2.59)
(2.59)
Если функция Ляпунова 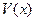 является решением уравнения Гамильтона-Якоби-Беллмана
является решением уравнения Гамильтона-Якоби-Беллмана
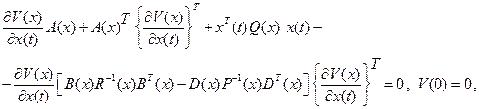 (2.60)
(2.60)
то управления 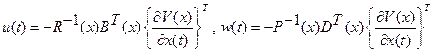 есть оптимальные управления к множеству допустимых управлений, производящих траектории, которые целиком расположены в X .
есть оптимальные управления к множеству допустимых управлений, производящих траектории, которые целиком расположены в X .
Пусть 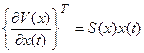 , где симметричная положительно определенная матрица
, где симметричная положительно определенная матрица 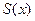 является решением уравнения Риккати с параметрами, зависящими от состояния (SDRE),
является решением уравнения Риккати с параметрами, зависящими от состояния (SDRE),
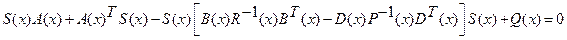 .(2.62)
.(2.62)
Тогда условие асимптотической устойчивости (2.59) будет иметь вид
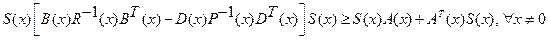 .(2.61)
.(2.61)
Добавление 2.7.1.В задаче дифференциальной игры условие асимптотической устойчивости вида (2.59) дополняется условием: матрица
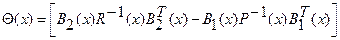 (2.63)
(2.63)
должна быть, по крайней мере, положительно полуопределенной.
Следует заметить, что при сделанных предположениях управления (2.50) обеспечивают локально асимптотические свойства стабилизации SDC-представлению нелинейной системы. Однако, асимптотическая стабилизация может не иметь место в исходной нелинейной системы с синтезированными SDRE-методом управлениями и произвольным начальным состоянием 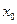 (глобальная асимптотическая стабилизация).
(глобальная асимптотическая стабилизация).
В качестве альтернативы глобальной асимптотической устойчивости, которую обычно трудно достичь и/или доказать, желательно иметь
возможность оценки области притяжения для асимптотической устойчивости системы с регулятором, синтезированным с использованием SDRE-метода. Это область в пространстве состояний, которая образуется траекториями асимптотически устойчивой системы управления, начинающимися из любого начального состояния системы, принадлежащего заданной области 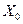 , в момент
, в момент 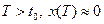 .
.
Для отыскания условий, которым должна отвечать область притяжений, введем в рассмотрение две системы
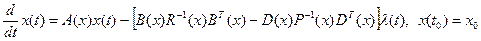 , (2.64)
, (2.64)
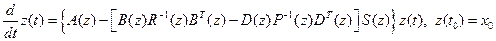 , (2.65)
, (2.65)
где 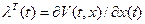 и положительно определенная матрица
и положительно определенная матрица 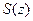 − поточечное решение алгебраического уравнения Риккати (2.62).
− поточечное решение алгебраического уравнения Риккати (2.62).
Пусть 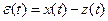 . Тогда
. Тогда
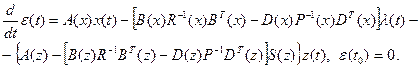 (2.66)
(2.66)
Очевидно, что при 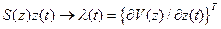 будет
будет 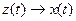 , т.е.
, т.е. 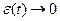 .
.
В окрестности нуля для стабилизированных систем (2.63) и (2.64) выполняется следующее соотношение
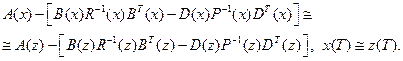 (2.67)
(2.67)
Уравнение ошибки при этом (2.66) будет иметь вид
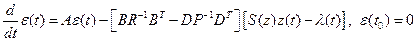 . (2.68)
. (2.68)
Введем функцию Ляпунова
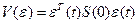 ,
,
где положительно определенная матрица 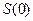 − решение алгебраического уравнения (2.62) при
− решение алгебраического уравнения (2.62) при 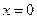 . Тогда вблизи нуля для траекторий, порождаемых решениями уравнений (2.64), (2.65), будем иметь
. Тогда вблизи нуля для траекторий, порождаемых решениями уравнений (2.64), (2.65), будем иметь
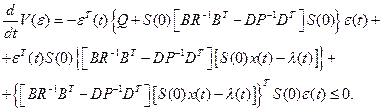
Так как 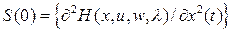 при
при 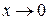 ,
,
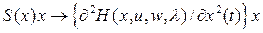 и
и 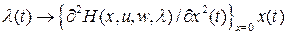 , то для тех начальных условий, для которых
, то для тех начальных условий, для которых 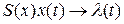 при
при 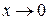 , условие
, условие
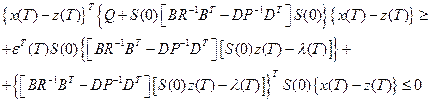 (2.69)
(2.69)
определяет область притяжения стабилизируемых траекторий системы, начинающихся из 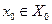 , для всех
, для всех 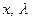 , удовлетворяющей канонической системе
, удовлетворяющей канонической системе
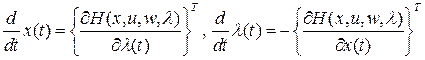 .
.
Дата добавления: 2019-10-16; просмотров: 594;
