Дифференциальная игра: общее решение

SDRE-метод синтеза управляющих воздействий

Постановка задачи

Проблема управления линейными объектами (Linear Quadratic Regulator, LQR) в различных постановках с квадратичными критериями качества с постоянными матрицами штрафа хорошо изучена, и разработанные алгоритмы математического конструирования регуляторов широко используются при решении практических задач. В основе синтеза оптимальных управлений лежат, в зависимости от задачи, дифференциальное или алгебраическое уравнения Риккати (Differential Riccati Equations, DRE; Algebraic Riccati Equations, ARE). Теоретические основы решения линейно-квадратических задач в ряде случаев могут быть применены при синтезе управляющих воздействий для нелинейных систем.

Одним из многообещающих и быстро развивающихся методов для проектирования нелинейных регуляторов является уравнение Риккати, параметры которого зависят от состояния объекта и матриц штрафа функционала качества (State Dependent Riccati Equations, SDRE). Впервые проблема управления нелинейными объектами с их эквивалентном представлением в виде линейных моделей (State Dependent Coefficient, SDC) с параметрами, зависящими от состояния, и функционалами, матрицы штрафа которых также зависят от состояния объекта, была сформулирована в начале 60-ых годов 20-го столетия [41]. Разработка предложенного метода была продолжена в работах [38, 39]. С конца 90-х годов метод привлекает все большее внимание со стороны ученых и практиков.

Преобразование исходного нелинейного дифференциального уравнения, которое описывает исходную систему управления, в систему с линейной структурой, но с параметрами, зависящими от состояния, и использование квадратичного функционала качества позволяют при синтезе управления осуществить переход от уравнения Гамильтона-Якоби-Беллмана к уравнению типа Риккати с параметрами, зависящими от состояния. Это и составляет основу SDRE-метода синтеза оптимальных нелинейных систем управления.

К концу первой декады 21-го столетия появилось не только многообразие опубликованных теоретических работ, но и примеры успешного использования SDRE-метода при построении систем управления подвижными объектами, производственными и экологическими системами. К этим примерам относятся решения задач управления искусственной человеческой поджелудочной железой, контроля положения космического корабля, химического реактора и многие другие.

В рамках 17-го Симпозиума IFAC по Автоматическому управлению в Космосе 2007 (Тулуза, Франция) была организована специальная секция, на которой обсуждалось состояние и перспективы развития теории и практики SDRE-метода проектирования управлением нелинейными объектами [22, 28, 37]. Работы, в которых рассматривались вопросы применения этого метода, можно увидеть и среди докладов 17 (2008, Сеул) и 18 (2011, Милан) конгрессах IFAC.

Несмотря на имеющиеся достаточно убедительные примеры применения SDRE-метода, остается множество проблем, связанных с ограничениями, накладываемыми на систему, неоднозначностью эквивалентных преобразований исходной системы, построение эффективных алгоритмов решений матричных уравнений Риккати с параметрами, зависящими от состояния, в темпе функционирования системы управления.

В данной книге задача управления нелинейным объектом, подвергающимся воздействию неконтролируемых возмущений, будет рассматриваться в более общем виде, а именно в ключе дифференциальной игры, что позволит обобщить ряд ранее опубликованных теоретических результатов. Это позволит получить достаточно конструктивные решения в ряде постановок задач управления. Такой класс задач принято относить к управлениям с гарантирующим результатом.

Пусть нелинейный управляемый и наблюдаемый объект описывается векторным дифференциальным уравнением

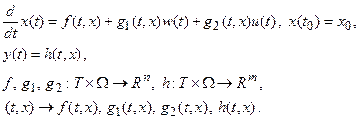(2.1)

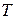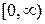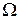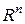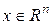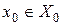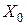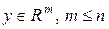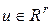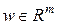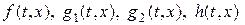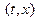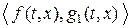Здесь − интервал ; −область (открытое связанное множество) , содержащая начало; −состояние системы; , − область возможных начальных состояний системы; − выход системы; −управление, подлежащее нахождению; −неизвестное возмущение; матрицы действительны и непрерывны. Предполагается, что при всех пары и 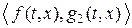являются управляемыми, пара 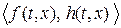наблюдаемой. Кроме того, функции 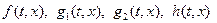будем предполагать достаточно гладкими, чтобы через любые 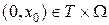проходило одно и только одно решение (2.1) 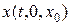и был бы единственный соответствующий выход системы .

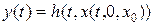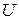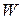Рассматривая задачу синтеза закона управления, как дифференциальную игру двух игроков и на 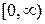, введем функционал

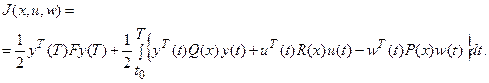(2.2)

Матрицы 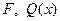могут быть положительно полуопределенными; матрицы 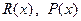− положительно определенные. Дополнительным требованием является требование детектируемости. Предположим, что пара 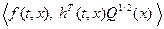детектируема при всех 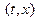. Требования к значениям параметров матриц 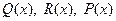будут определены далее.

Задача заключается в построении для игроков 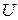и 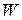оптимальных стратегий с обратной связью, реализуемых в темпе функционирования объекта. Ограничения на управляющие воздействия учитываются при назначении матриц 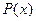и .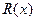

Дифференциальная игра: общее решение

Дадим вначале некоторые комментарии по вопросу существования решения задачи. Предполагая, что функции 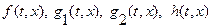, 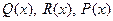достаточно гладкие, 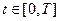, введем функцию стоимости игры

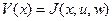, (2.3)

где 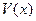дифференцируемая функция при любых допустимых стратегиях игроков 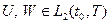. Уравнение Гамильтона-Якоби будет иметь вид

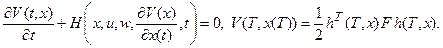(2.4)

Здесь 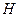− гамильтониан

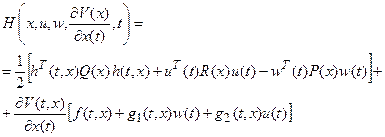(2.5)

При незаданном времени окончания переходного процесса (задача стабилизации), т.е. пр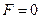и и 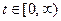, учитывая, что 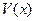в явном виде не зависит от времени, будем иметь

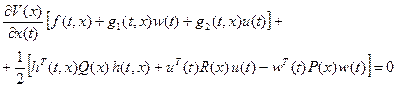(2.6)

с граничным условием 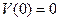, так как .

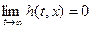Перепишем (2.6) в виде

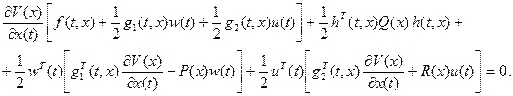(2.7)

Определим управления 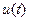и 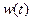с точностью до 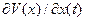так, чтобы последние два слагаемых (2.7) равнялись нулю, т.е.

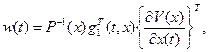
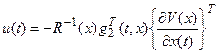. (2.8)

Тогда уравнение Гамильтона-Якоби примет вид

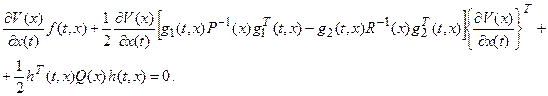(2.9)

Исходная система с управлениями (2.8) определяется выражением

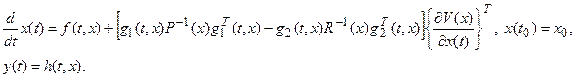
Отметим, что при

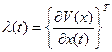, (2.10)

уравнение (2.9) вместе с канонической системой

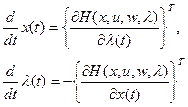
образуют необходимые условия оптимальности системы (2.1) с управлениям

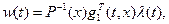
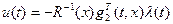. (2.11)

Как будет показано дальше, матрицы 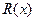и 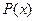, при всех 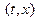и параметрах системы 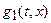и 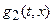, должны назначаться так, чтобы матрица

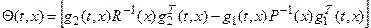(2.12)

была бы положительно полуопределенной.

Очевидно, что для реализации управлений вида (2.8) необходимо решить уравнение (HJ) в частных производных, что является самостоятельной сложной задачей.

Кроме того,

1. 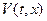может и не существовать;

2. если и можно найти 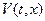, то нет гарантии, что функция времени 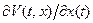- градиент 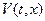, вычисленный в точке 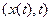, есть дополнительный вектор 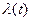, соответствующи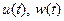й и 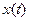т.е. нет уверенности, что существует зависимость

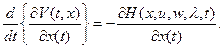(2.13)

Пусть 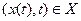, где Х – область, содержащая S. Обозначим минимум (наибольшую нижнюю границу) функции 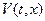через :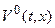

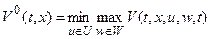. (2.14)

Управления 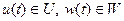, при котором достигается 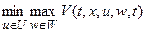, обозначим через .

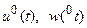Таким образом, 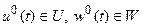- допустимые и в силу (2.14) оптимальные управления.

Предположим также:

1. 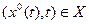для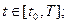

2. 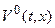непрерывно дифференцируема на X.

В силу оптимальности 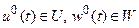можно записать, что:

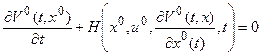(2.15)

для 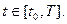Таким образом, при предположениях 1 и 2 уравнение (2.15) является дополнительным необходимым условием оптимальности.

Если на правом конце задано условие 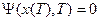, то

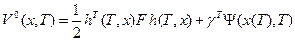(2.16)

и вектор 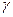, удовлетворяет следующему соотношению:

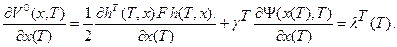
Покажем, что при некоторых предположениях относительно управляющих воздействий, справедлива зависимость (1).

Лемма 2.2.1

Пусть имеются допустимые управления 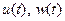и при этом:

1. 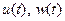переводят 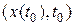в S;

2. имеется траектория 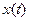, соответствующая 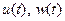, то 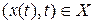для всех ;

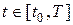3. 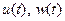удовлетворяют соотношению 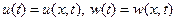для всех 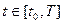, где 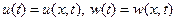являются решением уравнения Гамильтона-Якоби, то 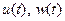есть оптимальные управления к множеству допустимых управлений, производящих траектории, которые целиком расположены в X ,

тогда .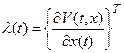

Доказательство

Для сокращения записи введем обозначение

,

.

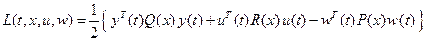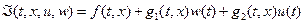Тогда

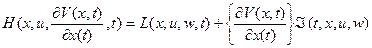, (2.17)

и

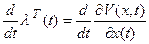(2.18)

Продифференцируем выражение (2.18) по 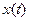. Будем иметь

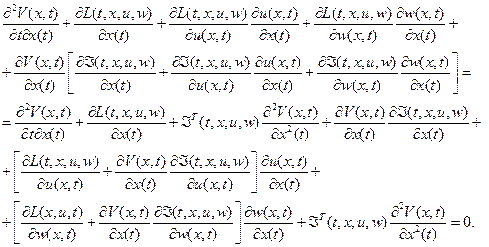(2.19)

Выражения в квадратных скобках при 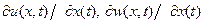на оптимальной траектории обращаются в нуль. Используя (2.19), преобразуем (2.18) к виду

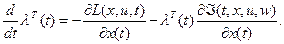(2.20)

Кроме того, условие (2.16) определяет значение 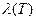. Отметим, что уравнение (2.20) совместно с уравнением (2.16) образует систему уравнений Эйлера – Лагранжа.

Таким образом, если имеются допустимые управления 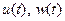и при этом:

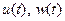· переводят 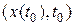в S;

· имеется траектория 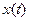, соответствующая 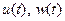, то 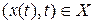для всех ;

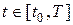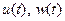· удовлетворяют соотношению 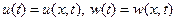для всех 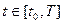, где 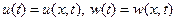являются решением уравнения Гамильтона-Якоби, то 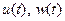есть оптимальные управления к множеству допустимых управлений, производящих траектории, которые целиком расположены в X .

Рассмотрим каждое из составляющих необходимых условий оптимальности.

1. Первое уравнение (для 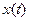) канонической системы

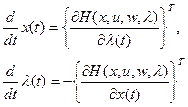
есть в точности исходная система уравнений, описывающая объект управления, которая не зависит от дополнительной переменной 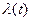. Второе уравнение (для 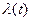) канонической системы описывает движение нормали к гиперплоскости вдоль оптимальной траектории. Уравнение имеет множество решений, каждое из которых описывает движение соответствующей нормали к гиперплоскости вдоль оптимальной траектории. Каноническая система имеет решения вдоль любой траектории системы, а не только для оптимального управления.

2. Первое свойство дополнительной переменной 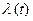состоит в том, что оптимальное управление является точкой стационарности гамильтониана (2.5).

3. Формулировка необходимых условий не зависит от типа области S значений конечных состояний системы и от того, фиксировано или нет время окончания переходного процесса.

4. Необходимые условия оптимальности, сформулированные в виде поведения гамильтониана на оптимальной траектории, непосредственно зависят от того, является ли время окончания переходного процесса фиксированным или нет. Гамильтониан постоянен вдоль оптимальной траектории лишь в случае, когда система и функционал явно не зависят от времени.