Модели макромолекул
1. Модель свободно сочлененной цепи (модель ССЦ)
Эта модель является наиболее идеализированным представлением о макромолекуле.
Положения, позволяющие построить данное представление:
а) может происходить относительно свободное вращение звеньев друг относительно друга;
б) взаимодействия между заместителями в макромолекуле отсутствуют;
в) валентный угол не фиксирован;
г) расстояние между атомами строго фиксировано;
д) объемами атомов углерода пренебрегают.

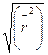
Рис. 16.2. Модель свободно сочлененной цепи (ССЦ)
Удобной статистической характеристикой конформации цепи является 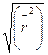 - среднее квадратичное расстояние между концами цепи. Математическое рассмотрение этой модели приводит к следующему выражению:
- среднее квадратичное расстояние между концами цепи. Математическое рассмотрение этой модели приводит к следующему выражению:
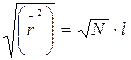 , (16.1)
, (16.1)
где N – число звеньев в цепи, а l – длина одного звена
Полная длина цепи представляет собой произведение этих величин:
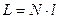 (16.2)
(16.2)
Макромолекулу можно характеризовать степенью свернутости:
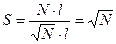 (16.3)
(16.3)
Степень свернутости представляет собой потенциальную возможность изменения размеров макромолекулы.
Количество звеньев эквивалентно степени полимеризации, поэтому при увеличении степени полимеризации возможность изменения размеров увеличивается.
Пример: при степени полимеризации 102 макромолекула может изменять свой размер в 10 раз, при 104 – в 100 раз.
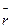 соответствует наиболее вероятному значению r, т.е. среднему значению
соответствует наиболее вероятному значению r, т.е. среднему значению
Распределение макромолекул по значениям расстояний между концами цепи является гауссовым:
 W(r)
W(r)
rmax r
Рис. 16.3. Распределение макромолекул по значениям расстояний между концами цепи
поэтому клубок, образуемый макромолекулой, часто называют гауссовым клубком.
2. Модель с фиксированным валентным углом
Модель представляется в следующем виде:

2 θ
α
1 3
Рис. 16.4. Модель с фиксированным валентным углом
вращение происходит свободно, но только по образующим конуса.
Средне-квадратичное расстояние равно в этом случае:
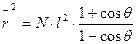 (16.4)
(16.4)
Для α = 109,5◦ в полиэтилене θ = 180◦ - α = 71◦, cosθ = 1/3 и 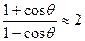 , поэтому можно заключить, что по сравнению с предыдущей моделью клубок немного разбухает (в ~ 1,4 раза), жесткость молекулы увеличивается, но зависимость
, поэтому можно заключить, что по сравнению с предыдущей моделью клубок немного разбухает (в ~ 1,4 раза), жесткость молекулы увеличивается, но зависимость
|
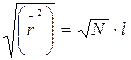 (16.5)
(16.5)
сохраняется.
3. Модель с заторможенным вращением
Эта модель аналогична предыдущей модели, вводится лишь положение о том, что происходит заторможенное вращение, некоторые конформации недоступны из-за того, что энергии теплового движения недостаточно для их реализации.
Поэтому вводится поправка, учитывающая углы заторможенного вращения, при которых реализуются возможные конформации:
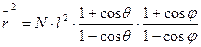 (16.6)
(16.6)
Наконец, переход к поворотно-изомерной модели, учитывающей не только фиксированные транс- и гош-конформации соседних звеньев, но и различия в энергиях между ними, также не приводит к нарушению зависимости 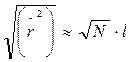 , а лишь влияет на величину коэффициента пропорциональности, который будет зависеть от разности энергий транс- и гош-конформаций.
, а лишь влияет на величину коэффициента пропорциональности, который будет зависеть от разности энергий транс- и гош-конформаций.
Таким образом, переходим от идеализированной модели к более реальной модели.
Рассмотрим участок цепи:

2 4
1 3
Рис. 16.5. Модель с заторможенным вращением
Здесь еще сохраняется корреляция положения атома 1 относительно атома 4.
Существует некоторый атом n на, котором корреляция теряется, т. е. можно считать, что он движется независимо от атома 1. Участки, состоящие из n атомов, в которых атом n начинает перемещаться независимо от атома m, называются сегментами (сегментами Куна). Таким образом, макромолекулу можно условно разделить на сегменты, перемещающиеся независимо друг относительно друга.
Исходя из этого, можно применить модель свободно-сочлененной цепи для любой реальной цепи, заменяя величину сегмента Куна, равную длине химической связи в модели ССЦ на больший отрезок цепи, соответствующий реальному сегменту Куна для данного полимера.
Независимо от способов разбивки на участки контурная длина цепи L не изменяется (она определяется лишь числом мономерных остатков, образующих макромолекулу).

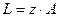
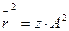 (16.7)
(16.7)
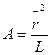 , z – число сегментов, А – длина сегмента, L – контурная длина цепи
, z – число сегментов, А – длина сегмента, L – контурная длина цепи
Величина 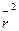 определяется методом светорассеяния.
определяется методом светорассеяния.
На основании экспериментальных данных можно составить следующую таблицу:
Таблица 16.1.
Величины длины звена и числа мономерных звеньев в сегменте
| Полимер | Длина звена А, А˚ | Число мономерных звеньев в сегменте |
| Полидиметилсилоксан | 4,9 | |
| Полипропилен | 21,7 | 8,6 |
| Полистирол | 7,9 | |
| Поливинилхлорид | 29,6 | 11,7 |
| Тринитроцеллюлоза |
Гибкость – способность макромолекулы изменять свою форму под действием теплового движения.
Гибкость макромолекулы связана с величиной сегмента: чем меньше величина сегмента, тем больше гибкость молекулы.
Таким образом, длина сегмента Куна является важной характеристикой макромолекулы.
Наглядное представление о конформации реальных макромолекул различной длины можно получить, построив с помощью компьютера их траектории в пространстве. Так для воображаемой цепи полиэтилена ее конформация (траектория) строится путем последовательного размещения каждого последующего звена с учетом длины связи С–С, угла поворота относительно транс-конформации (φ = 0) в гош-конформации (± 115◦С) и разности энергий транс- и гош-конформаций.
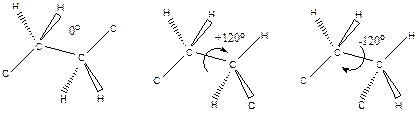
Результаты математического эксперимента представлены в таблице 16.2. для трех длин цепей 50, 500 и 3000 связей.
Таблица 16.2.
Результаты математического эксперимента для цепей полиэтилена различной длины
| n | Vгл/Vклуб | 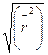 /Lтранс /Lтранс
|
| 0,1 | 0,25 | |
| 0,03 | 0,12 | |
| 0,01 | 0,02 |
где Vгл и Vклуб – объемы молекулы в конформации плотных глобул и занимаемый объем в рассчитанной конформации, а Lтранс и 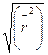 - расстояние между концами цепи в конформациях транс-зигзага и рассчитанной траекторией цепи. Видно, что конформации линейных макромолекул очень «рыхлые», фрагментами молекулы заполнена лишь небольшая часть пространства, в котором она находится, и плотность заполнения пространства уменьшается с ростом молекулярной массы, а расстояние между концами цепи оказывается значительно меньше длины полностью вытянутой цепи в соответствии с предсказаниями теории.
- расстояние между концами цепи в конформациях транс-зигзага и рассчитанной траекторией цепи. Видно, что конформации линейных макромолекул очень «рыхлые», фрагментами молекулы заполнена лишь небольшая часть пространства, в котором она находится, и плотность заполнения пространства уменьшается с ростом молекулярной массы, а расстояние между концами цепи оказывается значительно меньше длины полностью вытянутой цепи в соответствии с предсказаниями теории.
Дата добавления: 2019-07-26; просмотров: 1431;
