Усилия, действующие на судно при произвольном движении
Кинематические параметры движения
Судна
Для точной оценки местоположения судна и особенностей его поведения при маневрировании необходимо прежде всего установить кинематическую связь между отдельными параметрами его движения .
В общем случае судно, как управляемая система, при произвольном движении обладает шестью степенями свободы. Однако, при решении практических задач управления водоизмещающими судами обычно исследуют лишь движение в горизонтальной плоскости, совпадающей с невозмущенной поверхностью воды.
Для удобства анализа изменения параметров движения судна обычно используют две системы прямоугольных координат (рис.2).:
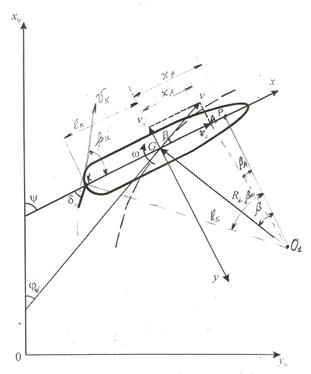
Рис. 2. Кинематический параметры криволинейного движения судна
неподвижную, связанную с Землей – XоOУо и подвижную, связанную с основными осями симметрии судна – XGУ.
Начало подвижной системы координат расположено в центре масс (G), ось X совпадает с диаметральной плоскостью судна (Д.П.) и имеет положительное направление в нос, а ось У – по нормали к ней и её положительное направление – в
сторону перекладки рулевого органа.
Неподвижная система координат расположена так, что положительное направление оси (Xо) берется в сторону первоначального (до начала маневра) прямолинейного движения судна, а ось Уо – по нормали к ней с положительным направлением также в сторону перекладки рулевого органа. Полагаем, что в начальный момент маневрирования обе системы координат совпадают.
Неподвижная система координат обычно используется только для определения местоположения судна в любой момент времени (точно также, как координаты судна в навигации) и построения траектории движения какой-либо точки на плоскости. Поскольку судно является не точечным объектом, а имеет линейные размеры, то его мгновенное положение в пространстве определяется дополнительными координатами:
- углом курса Ψ (или угол поворота), это угол между осью OXо и диаметральной плоскостью судна (Д.П.);
- углом дрейфа β (угол между вектором линейной скорости в рассматриваемой точке и Д.П.; обычно в рассмотрение вводят ещё угол скорости 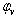 это угол между осью OXо и направлением касательной к траектории движения вектором линейной скорости. (В навигации этот угол называют путевым углом). Он удобен для определения координат траектории криволинейного движения.
это угол между осью OXо и направлением касательной к траектории движения вектором линейной скорости. (В навигации этот угол называют путевым углом). Он удобен для определения координат траектории криволинейного движения.
Все эти углы связаны очевидным соотношением:
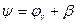 (1)
(1)
Известно, что движение судна, как и любого твердого тела, по произвольной траектории всегда может быть представлено как результат двух простых видов движения: поступательного с линейной скоростью 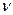 , которая всегда направлена по касательной к траектории вращательного движения с угловой скоростью
, которая всегда направлена по касательной к траектории вращательного движения с угловой скоростью 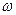 относительно вертикальной оси, проходящей через центр тяжести судна.
относительно вертикальной оси, проходящей через центр тяжести судна.
Под угловой скоростью поворота судна понимают изменение угла курса в единицу времени т.е.
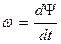
| (2) |
Дифференцируя по времени уравнение (1) с учетом (2) получим
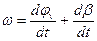
| (3) |
Траекторию криволинейного движения судна всегда можно представить отрезком длины окружности определенного радиуса (или нескольких отрезков разной кривизны, если движение судна носит неустановившийся характер). Из курса аналитической геометрии известно, что радиус кривизны любой дуги определяется выражением:
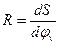
| (4) |
где 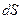 - элементарная длина дуги;
- элементарная длина дуги;
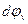 - элементарный угол поворота.
- элементарный угол поворота.
Применительно к траектории криволинейного движения величина 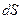 определяет расстояние, пройденное судном, т.е.:
определяет расстояние, пройденное судном, т.е.:
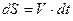
| (5) |
С учетом этого, выражение (4) можно представить в виде:
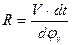
| (6) |
Преобразуя выражение (6) путем разделения переменных получим:
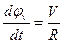
| (7) |
Подставляя (2) и (7) в уравнение (3) имеем:
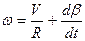
| (8) |
Полученное выражение определяет связь между параметрами поступательного и вращательного движения судна по любой произвольной криволинейной траектории.
Оно широко используется в практике управления судном. Исследования показали, что доля величины 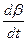 в составе значения угловой скорости на судах внутреннего и река-море плавания не превышает 7 %. В связи с этим, с достаточной для практических целей точностью можно пользоваться упрощенным приближенным выражением
в составе значения угловой скорости на судах внутреннего и река-море плавания не превышает 7 %. В связи с этим, с достаточной для практических целей точностью можно пользоваться упрощенным приближенным выражением
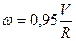 (9)
(9)
где 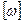 - град/мин;
- град/мин;
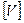 - км/ч;
- км/ч;
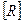 - км;
- км;
которое позволяет с достаточной точностью проводить суда по криволинейным участкам определенного радиуса судового хода с заданной угловой скоростью.
Точность проводки увеличивается, если на судне в составе навигационного оборудования имеется прибор УСП (указатель скорости поворота).
Однако, при оценке безопасности движения не следует забывать, что угол дрейфа имеет разное значение для различных точек по длине судна.
Рассмотрим прямоугольный треугольник O1PG(рис.2)
Так, для произвольной точки A справедливо выражение:
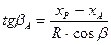
| (10) |
где 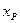 и
и 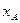 - соответственно абсцисса точки P и точки A
- соответственно абсцисса точки P и точки A
относительно центра масс судна G
С учетом того, что
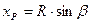
| (11) |
выражение (10) можно представить в виде
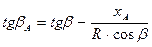
| (12) |
Из выражения (12) нетрудно видеть, что при наложении рассматриваемой точки в носовой части судна от центра тяжести (увеличении аппликаты ХА) угол дрейфа уменьшается. Такая точка на диаметральной плоскости, в которой угол дрейфа равен нулю ( 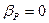 ) называется «полюсом поворота» (или «центром вращения» - Pivot Point) В этой точке направление вектора линейной скорости совпадает с Д.П. судна. Для всех точек, которые лежат впереди «полюса поворота» угол дрейфа имеет отрицательное значение.
) называется «полюсом поворота» (или «центром вращения» - Pivot Point) В этой точке направление вектора линейной скорости совпадает с Д.П. судна. Для всех точек, которые лежат впереди «полюса поворота» угол дрейфа имеет отрицательное значение.
При практическом маневрировании очень важно знать величину радиуса поворота кормового перпендикуляра судна, который определяет величину потребной акватории для разворота судна. Его величина определится из совместного решения прямоугольных треугольников 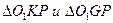 по очевидному выражению
по очевидному выражению
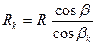
| (13) |
Поскольку скорости точек судна пропорциональны радиусам кривизны, то
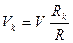
| (14) |
Выражение (14) является математическим объяснением известного в среде судоводителей термина «раскатка кормы» (когда на повороте корма как бы «забегает»-«раскатывается» в сторону, противоположную повороту вокруг полюса поворота). При этом угол дрейфа в корме судна равен
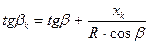
| (15) |
В настоящее время существует достаточный разброс мнений о точном местонахождении полюса поворота. Более подробно данный вопрос будет рассмотрен ниже.
При практических расчетах управляемости возникает необходимость определения траектории движения судна, т.е. отыскания координат центра масс в неподвижной системе координат и угла курса в произвольный момент времени.
В этом случае, при известных значениях кинематических параметров движения 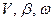 имеем (см. рис.2)
имеем (см. рис.2)
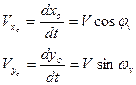
| (16) |
Интегрируя выражение (16) с учетом (1) имеем:
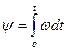 ; ;
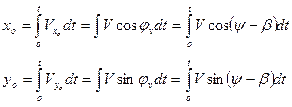
| (17) |
Параметры движения могут быть определены не только в центре масс судна, но и в любой его точке А.
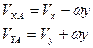
| (18) |
Усилия, действующие на судно при произвольном движении
В процессе выполнения того или иного маневра судно находится под воздействием нескольких сил, которые зависят от геометрических размеров судна, обводов корпуса, эффективности ДРК и параметров движения. Кроме того, в общем случае, эти силы зависят также от числа Фруда, которое характеризует волнообразование и числа Рейнольдса, которое определяет характер вязкостного сопротивления обтекающего потока.
Однако практикой установлено, что режим обтекающего судно потока является турбулентным. При этом влияние числа Рейнольдса сравнительно невелико. Число Фруда в реальном диапазоне скоростей транспортных судов не превышает 0,3. При таких значениях действующие на судно силы мало от него зависят.
В связи с этим, для упрощения поставленной задачи, их влиянием обычно пренебрегают.
Силы и моменты по природе их возникновения могут быть подразделены на три категории:
- силы и моменты, обусловленные собственной инерцией судна;
- силы и моменты, обусловленные инерцией воды, окружающей судно и возмущаемой его движением;
- вязкостные (неинерционные) силы и моменты, возникновение которых обусловлено влиянием вязкости воды (гидродинамические силы корпуса и рулевых органов).
Силы первых двух категорий определяют аналитическим путем. Силы третьей категории, как правило, определяются экспериментально.
Как уже отмечалось, при определении сил и моментов, действующих на движущееся судно, рассматривают лишь плоское движение. Силы веса и поддержания, взаимодействие которых определяется законом Архимеда, при определении маневренности не учитываются, т.к. они не оказывают влияние на движение судна в горизонтальной плоскости.
В условиях прямолинейного движения, при отсутствии ветра и течения, на судно действуют две категории сил (рис3)
- совокупная полезная тяга судовых движителей, равнодействующая которых направлена в сторону движения и располагается в Д.П. судна(Ре);
- силы сопротивления воды и воздуха движению, которые направлены в сторону, противоположную направлению движения, а их равнодействующая также располагается на Д.П. судна.
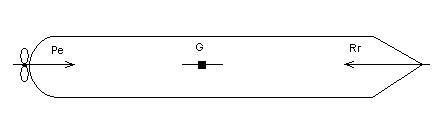
Рис.3 Силы действующие на судно при прямолинейном движении
При установившемся равномерном движении полезная тяга движителей равна величине сопротивления воды движению
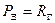 (19)
(19)
Как показано на рис.4, это равенство при определенной частоте вращения движителей соответствует строго определенной скорости движения, т.е.
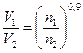
| (20) |
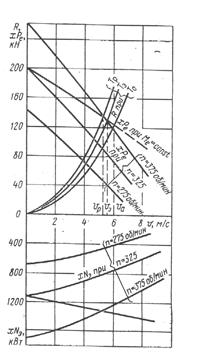
Рис.4. График скоростных характеристик грузового теплохода грузоподъемностью 5300 т
При неустановившемся прямолинейном движении к силам 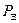 и Р Гдобавляется сила инерции
и Р Гдобавляется сила инерции 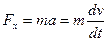
При ускоренном движении (разгон судна) 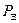
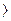 Р Г, сила инерции проявляется в виде дополнительного сопротивления.
Р Г, сила инерции проявляется в виде дополнительного сопротивления.
При замедленном (выбег судна) она является движущей силой.
Уравнение прямолинейного движения судна в общем случае имеет вид:
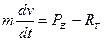
| (21) |
Это уравнение характеризует любой маневр судна на прямом курсе (маневр скоростью).
Изменение курса осуществляется, как правило, за счет перекладки рулевых органов (рис.5).
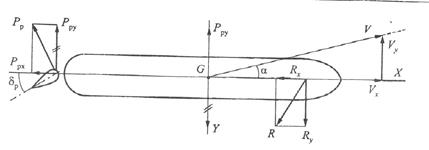
Рис.5 Силы, действующие на судно с переложенным рулем в начальной стадии циркуляции
После перекладки рулевого органа на нём возникает сила давления воды 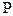 , которую можно разложить на две составляющие
, которую можно разложить на две составляющие 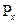 и
и 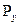 .
.
Составляющая сила 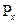 , направлена в сторону, обратную движению, увеличивает сопротивление воды движению судна. Поперечная составляющая
, направлена в сторону, обратную движению, увеличивает сопротивление воды движению судна. Поперечная составляющая 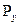 кормы образует поворачивающий момент
кормы образует поворачивающий момент 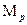 относительно центра масс. На корпусе судна, движущемся под углом к набегающему потоку (т.е. с углом дрейфа) возникают гидродинамические силы, равнодействующая которых в начальный момент маневра находится в носовой части судна (рис.5)
относительно центра масс. На корпусе судна, движущемся под углом к набегающему потоку (т.е. с углом дрейфа) возникают гидродинамические силы, равнодействующая которых в начальный момент маневра находится в носовой части судна (рис.5)
Под действием рулевого момента судно будет отклоняться от линии первоначального курса с некоторой угловой скоростью
. Одновременно с появлением начальной угловой скорости появляется центробежная сила инерции ( 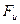
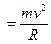 ),(рис. 6) приложенная в центре масс и действующая по радиусу траектории по нормали к вектору скорости. Как только диаметральная плоскость (Д.П.) судна начинает отклоняться от линии вектора скорости первоначального движения, симметричность обтекания корпуса судна нарушается.
),(рис. 6) приложенная в центре масс и действующая по радиусу траектории по нормали к вектору скорости. Как только диаметральная плоскость (Д.П.) судна начинает отклоняться от линии вектора скорости первоначального движения, симметричность обтекания корпуса судна нарушается.
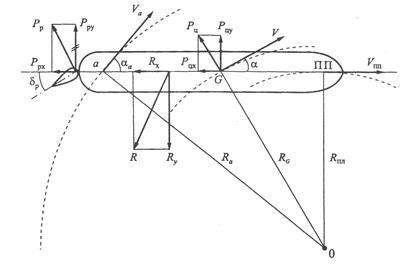
Рис.6 Силы действующие на судно при криволинейном движении на развитой стадии циркуляции
С появлением силы 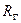 угловая скорость начинает быстро расти, т.к. её поперечная составляющая
угловая скорость начинает быстро расти, т.к. её поперечная составляющая 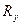 совместно с поперечной составляющей рулевой силы
совместно с поперечной составляющей рулевой силы 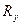 образуют пару сил. и поворачивающий момент резко возрастает.
образуют пару сил. и поворачивающий момент резко возрастает.
Управляемость судна определяется, в основном, взаимным расположением трех точек: центра масс ( G ), центра приложения равнодействующей всех сил реакции воды (Р Г) и центра приложения движущих сил (ДРК).
Дата добавления: 2019-07-26; просмотров: 1170;
