Лекция № 6. § 6 – 1 Взаимодействие прямых проводников.
Вообще говоря, силу действия на проводник с током, помещенный в магнитное пол, можно вычислить пользуясь законом Ампера, который был сформулирован на прошлой лекции. Однако для упрощения математических выкладок предположим, что величина поля определена заранее. Пусть это поле однородное, т.е. его значение одинаково во всех точках рассматриваемого пространства. Тогда сила, действующая на элемент тока, записывается в таком виде:
dF = IBdlsina,
где a - угол между направлением В и элементом тока Idl.
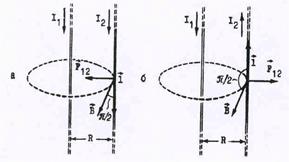 Рис.24. Взаимодействие двуз прямых
проводников.
Рис.24. Взаимодействие двуз прямых
проводников.
| Для конечного проводника длины L имеем: F = IBLsina. Наиболее простой вид эта формула приобретает для случая взаимодействия двух прямых проводников.Для простоты будем считать их бесконечными так, что поле, создаваемое про-водником, по которому проходит ток I1, во всех точках другого проводника с током I2 (см. рис.24), имеет одно и то же значение, если проводники параллельны друг другу. В этом случае сила, действующая на отрезок проводни- |
ка длиной L с током I2, равна F12 =BL I2, или, подставляя в эту формулу явное выражение для В, имеем:
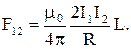 ( ◊ )
( ◊ )
Направление силы взаимодействия для параллельных и антипараллельных взаимодейству-ющих токов показано на рис.24. Из рисунка видно, что параллельные токи притягиваются, а токи с противоположным направлением отталкиваются друг от друга.
Формулу ( ◊ ) используют для определения единицы измерения силы тока – ампера. Пола-гая I1=I2 = 1A, R = 1M и L = 1M, можно вычислить, что сила взаимодействия равна 2´10-7Н, т.е. за единицу силы тока принимают такой ток, который, протекая по параллельным про-водам, отстоящим друг от друга на расстояние 1м, вызывает силу 2´10-7Н, действующую на единицу длины проводника.
§ 6 – 2 Действие магнитного поля на контур с током.
Пусть прямоугольная рамка, со сторонами a и b, обтекаемая током I, помещена в однородное магнитное поле индукции В, как показано на рис.25. Модули сил, действующих
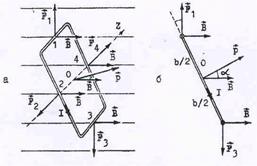 Рис.25. Действие магнитного поля
на рамку с током.
Рис.25. Действие магнитного поля
на рамку с током.
| на соответствующие стороны рамки равны: F1=F3 = IaB sin 900 = IaB, F2 = F4 IbBsin(90-a) =IbBcosa. Направления всех сил указаны на рисунке, откуда следует, что сумма всех сил, действу-ющих на рамку, равна нулю. Следовательно, центр масс должен оставаться в покое, если первоначально он был неподвижен. Однако суммарный момент сил оказывается отличным от нуля. Напомним, что момент силы М определяется век-торным произведением радиуса-вектора, проведен-ного от оси в точку приложения силы, на саму силу. Вычислим моменты всех сил относительно оси z, |
проходящей через центр рамки ( см. рис.25). Из рисунка видно, что моменты сил F2 и F4 равны нулю.Момент силы F1 M1 = F1sina b/2 = IB sina b/2 = (1/2)ISBsina, где ab = S – пло-щадь рамки. Момент силы F3 также равен М1, так что суммарный момент сил равен:
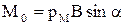 ,
,
где введенная величина рм =IS носит название магнитного момента рамки. Если магнитно-му моменту приписать векторные свойства, определяя его направление по правилу правого винта, движение оси которого определчется, в свою очередь, вращением винта в направле-нии обтекания рамки током, то общий момент сил, действующих на рамку, равен
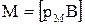 .
.
Этот момент стремится повернуть рамку к положению устойчивого равновесия, при котором магнитный момент рамки направлен вдоль направления поля.
§ 6 – 3 Сила Лоренца.
Опыт показывает, что сила, действующая на проводник с током, исчезает при выклю-чении тока,т.е. действие силы обусловлено движением электрических зарядов. Обращаясь к выражению силы тока I через движение отдельных зарядов, запишем:
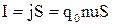 .
.
Тогда сила, действующая на проводник с током в однородном магнитном поле В может быть записана как
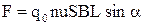 .
.
Из этого равенства можно определить силу, действующую на отдельный заряд q0 . Оцени- вая количество зарядов в проводнике N = nSL, нетрудно найти, что сила, известная в физике
   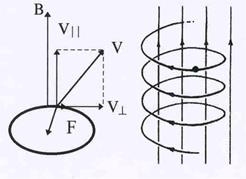 Рис.26. Действие силы Лоренца
на движущийся заряд.
Рис.26. Действие силы Лоренца
на движущийся заряд.
| как сила Лоренца, равна FЛ =q0uBsina.
Учитывая, что скорость направленного движения заря-дов в проводнике – u –вектор, и что направление силы определяется по правилу правого винта, можно опреде-лить силу Лоренца как
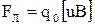 .
Сила Лоренца максимальна, когда скорость отдельного заряда перпендикулярна вектору В,и равна нулю, когда заряд движется параллельно силовым линиям магнит-ного поля. В первом случае заряд вращается по окруж-ности, радиус которой определяется законом Ньютона: .
Сила Лоренца максимальна, когда скорость отдельного заряда перпендикулярна вектору В,и равна нулю, когда заряд движется параллельно силовым линиям магнит-ного поля. В первом случае заряд вращается по окруж-ности, радиус которой определяется законом Ньютона:
|
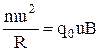 ;
; 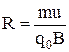 .
.
В общем случае, когда скорость заряда составляет с направлением поля произволь-ный угол a (см. рис.26.), траектория движения представляет собой винтовую линию, ось ко-торой совпадает с направлением поля. Движение заряда можно рассматривать в этом случае как сложение двух движений: вращения вокруг направления поля, обусловленного сос-тавляющей вектора скорости, нормальной к направлению В, и поступательного движения со скоростью, равной другой составляющей, параллельной полю.
Это свойство заряженных частиц вращаться в поперечном магнитном поле исполь-зуется для получения элементарных частиц с большими энергтями. Устройства, пред-назначенные для этого, называются циклотронами. Наиболее известны модификации этих устройств, которые называются синхрофазотронами. Усложнение конструкции ( и назва-ния) связано с тем, что в процессе ускорения частицы приобретают скорость, близкую к скорости света, вследствие чего их масса увеличивается, и они выпадают из условия синхронизма. Поэтому приходится увеличивать поле или уменьшать частоту напряжения.
§ 6 – 4 Электромагнитная индукция.
Из школьного курса физики известно, что при изменении магнитного поля, пронизы-вающего некую поверхность, ограниченную замкнутым проводящим контуром, в этом контуре возникает ЭДС, равная с обратным знаком скорости изменения магнитного потока. Это явление было откпыто в 1831 году известным английским ученым М. Фарадеем, и установленный им закон носит его имя. Определяя величину магнитного потока Ф как
Ф =BS cosa = 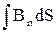 ,
,
где a - угол между направлением В и нормали к площади контура, закон Фарадея можно записать в виде:
E = - 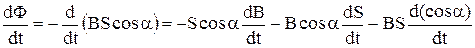 ;
;
откуда видно, что возникновение индукционноготока возможно при изменении либо вели-чины В, либо при изменении площади контура, либо при изменении ориентации контура (вращении) относительно направления магнитного поля. Магнитный поток прято измерять в Веберах. 1 Вебер = 1Тесла ´ м2.
Знак минус, стоящий перед производной магнитного потока отражает правило Лен-ца:индукционный ток направлен так, чтобы своим действием воспрепятствовать причине, его вызвавшей.
Проявлением индукционных токов являются токи Фуко, возникающие в массивных проводниках, помещенных в изменяющееся магнитное поле (например, в сердечниках трансформаторов). Для борьбы с этими токами сердечники набираются из очень тонких листов металла, разделенных прослойкой непроводящего лака.
§ 6 – 5 Самоиндукция.
Важным частным случаем электромагнитной индукции является самоиндукция, т.е. возникновение ЭДС индукции в самом проводнике, порождающим изменяющееся магнит-ное поле. В строгой теории электромагнетизма показано, что величина магнитного потока, окружающего проводник с током, пропорциональна силе этого тока Ф = L I, где коэффици-ент пропорциональности L носит название коэффициента самоиндукции или индуктив-ности.
Качественные соображения о пропорциональности между Ф и I вытекают из закона Био-Савара-Лапласа, где установлено, что В~ I. Значения L определяются геометрическими свойствами проводника. Единицей измерения L в системе СИ служит Генри.
1Генри =1Вебер/Ампер.
Учитывая взаимосвязь Ф и L, можно записать
Eсам = - 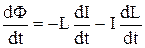 .
.
Если проводник не изменяет своей формы с течением времени, то dL/dt = 0, и
Eсам = - 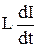 .
.
Для одного витка длинного соленоида Ф =ВS= m0 nIS, и, если полное число витков соле-ноида равно N= nlc, , то общий поток через весь соленоид Ф0 = Ф N = m0 n2lc IS, откуда
L = m0 n2lcS.
§ 6 – 6 Энергия магнитного поля.
Пусть имеется электрическая цепь, состоящая из источника постоянного тока, сопро-тивления и катушки индуктивности L. Предположим, что в некоторый момент времени источник мгновенно удаляется из цепи, которая остается замкнутой. Как следствие явления самоиндукции ток в цепи не исчезнет мгновенно, т.к. его будет поддерживать возникшая ЭДС самоиндукции. В процессе убывания тока сторонние силы, ответственные за явление самоиндукции, совершат некоторую работу. За малый промежуток времени dt, когда ток и ЭДС остаются практически неизменными, сторонние силы совершат работу dA = Eсамdq, где dq =Idt, или, используя выражение для ЭДС самоиндукции, dA= -Idt´L dI/dt, т.е.
dA=-LidI.
Полную работу сил можно найти, суммируя малые работы dA за весь период исчезновения тока:
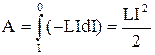 .
.
По закону сохранения энергии эта работа может быть совершена лишь за счет энергии W, которой обладает катушка с током, поэтому
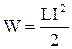 .
.
Эту энергию можно приписать магнитному полю катушки (соленоида). Считая соленоид достаточно длинным, можно использовать формулу, связывающую индукцию поля в соле-ноиде с током: B =m0 nI, откуда I = B/m0 n. Подставляя это соотношение, а также значение L для соленоида в выражение для энергии катушки, получаем:
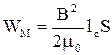 .
.
Тогда плотность магнитной энергии, т.е. энергии, приходящейся на единицу объема V=lcS,
равна
 w =
w = 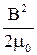 .
.
Дата добавления: 2019-07-26; просмотров: 533;
